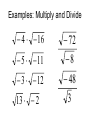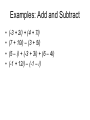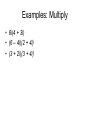* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Complex Numbers
Vincent's theorem wikipedia , lookup
Large numbers wikipedia , lookup
Infinitesimal wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Hyperreal number wikipedia , lookup
Location arithmetic wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Real number wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
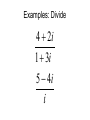
Section 8.7 Complex Numbers Overview • In previous sections, it was not possible to find the square root of a negative number using real numbers: • 81 is not a real number, or “n.a.r.n.” • In this section we will discover a way to find such square roots. • We will also learn about complex numbers and how to add, subtract, and multiply them. The imaginary number i • First, a definition: the imaginary number i is defined to be the square root of –1: i 1 • It follows that i 1 2 Definition • In general, if a is a real number and a > 0, then a i a Examples • Write each number as a product of a real number and i: 49 121 3 32 “Take the i out” • When multiplying and dividing square roots with a negative radicand, first use the definition to change the radical. a i a Examples: Multiply and Divide 4 16 5 11 3 12 13 2 72 8 48 3 Complex numbers • A number in the form a + bi, where a and b are real numbers and i 1 is called a complex number. • Complex numbers can be: 1. added (add the real parts together and the imaginary parts together) 2. subtracted (subtract the real parts and the imaginary parts) 3. multiplied (use the FOIL method and the fact 2 that i 1 ) Examples: Add and Subtract • • • • (-3 + 2i) + (4 + 7i) (7 + 10i) – (3 + 5i) (5 – i) + (-3 + 3i) + (6 – 4i) (-1 + 12i) – (-1 – i) Examples: Multiply • 6i(4 + 3i) • (6 – 4i)(2 + 4i) • (3 + 2i)(3 + 4i) Remember that “conjugate” thing? • Dividing complex numbers is very much like dividing radicals. • To divide complex numbers, multiply both the numerator and the denominator by the conjugate of the denominator. Examples: Divide 4 2i 1 3i 5 4i i