Download Algebra 1 - Davidsen Middle School

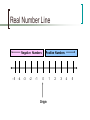
Algebra 1
Ch 2.1 – The Real Number
Line
Objective

Students will graph and compare real
numbers using a number line
Vocabulary






Throughout this course we will be working with
real numbers.
Real numbers can be pictured as points on a
horizontal line called the real number line
The point labeled 0 is called the origin
Points to the left of zero represent negative
numbers
Points to the right of zero represent positive
numbers
Zero is neither positive nor negative.
Real Number Line
Negative Numbers
-5
-4
-3
-2
-1
Positive Numbers
0
Origin
1
2
3
4
5
Vocabulary





In the real number line the scale marks are
equally spaced and represent integers.
Integers are the set of numbers that include
positive numbers, negative numbers and zero
The real number line has points that represent
fractions and decimals as well as integers.
The point that corresponds to a number is
called the graph of the number
Drawing the point is called graphing or
plotting the number
Graphing Real Numbers

To graph a real number:
1.
2.

Draw and label a number line
Find where the number is on the number
line and place a dot on the number
Let’s look at an example…
Example # 1

Graph the numbers ½ and -2.3 on a number line
1. Draw and label a number line
-5
-4
- 2.3
-3 -2
½
-1
0
1
2
3
4
5
Find where the number is on the number line and place a dot
on the number
2.

In this instance ½ is positive so it is to the right of zero
and less than 1

-2.3 is negative and to the left of zero 2.3 units
Comparing Real Numbers

Once points have been plotted on the
number line you can compare the
numbers.

Let’s look at an example
Note: Be careful here…there is more than 1 way to read
the comparison
Example # 2
Graph – 4 and – 5 on a number line. Then write 2
inequalities that compare the numbers
-5
-4
-3
-2
-1
1. Plot the point – 4
0
1
2
3
4
5
2. Plot the point – 5
•
On the graph – 5 is to the left of – 4 , so – 5 is less than – 4 which is
written as
–5<–4
•
On the graph – 4 is to the right of – 5 , so – 4 is greater than – 5 which is
written as
–4>–5
Comments



About a number line….it is expected
that you already know the following:
The further to the left of zero the
smaller the number is….
The further to the right of zero the
larger the number is….
Ordering Real Numbers





Often times you will be asked to order numbers
from least to greatest or greatest to least.
The goal here is to see if you understand the
relationship of the numbers…that is… do you
know which number is bigger or smaller than
another number
You can use the number line help you by
plotting the numbers and then reordering
them…
A strategy you can use here is to convert the
numbers to decimals and then plot and order
them as requested
Let’s look at an example…
Example # 3

Write the numbers in increasing order: - 2, 4 , 0, 1.5, ½ , - 3/2

First convert ½ and -3/2 to decimals. Which are .5 and – 1.5
respectively

Then plot each number on the number line:
- -2
3/2 or -1.5
-5
-4
-3
- 3/2
-2 -1
0 ½ or .51.5
½
0
4
1.5
1
2
3
4
5

Since you are numbering in increasing order read the number
line from left to right

The solution is: -2, -3/2, 0, ½ , 1.5, 4
Comments


In the previous example we converted
2 fractions into decimals to make it
easier to plot on the number line…
When writing your final solution to the
problem you should always use the
original numbers. In this case it was
½ and – 3/2 which are displayed in the
solution
Opposites


In a number line two numbers that are
the same distance from zero but in
opposite directions are called
opposites…
Let’s look at an example…
Example # 4
-5

-4
-3
-2
-1
0
1
2
3
4
5
In the above number line 2 and – 2 are
the same distance from zero but on
opposite sides. Therefore they are
considered opposites
Absolute Value




The absolute value of a number is simply
the distance the number is from zero on a
number line.
Vertical bars | | are used to represent the
absolute value of a number
The symbol |a| is read as the absolute
value of a.
The next slide shows a summary of
absolute value
Absolute Value
Example
If a is a positive number then the |a| = a
|3| = 3
If a is zero, then |a| = 0
|0| = 0
If a is a negative number, then the | - a| = a
|- 3| = 3
Notice: The absolute value of a number is NEVER negative
Comments



On the next couple of slides are some
practice problems…The answers are on the
last slide…
Do the practice and then check your
answers…If you do not get the same answer
you must question what you did…go back
and problem solve to find the error…
If you cannot find the error bring your work to
me and I will help…
Your Turn

1.
2.
3.
4.
Graph the numbers on a number line
then write 2 inequalities that compare the
numbers
-6 and 4
-6.4 and -6.3
-7 and 2
-2.7 and 3/4
Your Turn

5.
6.
7.
Draw a number line, plot the points and
then write the numbers in increasing
order
4.8, – 2.6, 0, -3, ½, - ½
7, - ½ , 2.4, - ¾, - 5.8, 1/3
3 ½ , 3.4, 4.1, -5, -5.1, -4 ½
Your Turn

8.
9.
10.
11.
Find the opposite of the number
10
-3
3.8
-2.5
Your Turn

Find the absolute value
12.
|7|
|-4|
|½|
|0| + 2
13.
14.
15.
Your Turn Solutions
1.
2.
3.
4.
5.
6.
7.
-6 < 4 or 4 > -6
-6.4 < -6.3 or -6.3 > -6.4
-7 < 2 or 2 > -7
-2.7 < ¾ or ¾ > -2.7
-3, -2.6, - ½ , 0, ½ , 4.8
-5.8, - ¾ , - ½ , 1/3, 2.4, 7
-5.1, -5, -4 ½ , 3.4, 3 ½ , 4.1
8.
9.
10.
11.
12.
13.
14.
15.
-10
3
-3.8
2.5
7
4
½
2
Summary



A key tool in making learning effective is being
able to summarize what you learned in a lesson in
your own words…
In this lesson we talked about graphing,
ordering and comparing numbers on the real
number line as well as opposites and absolute
value… Therefore, in your own words summarize
this lesson…be sure to include key concepts that
the lesson covered as well as any points that are
still not clear to you…
I will give you credit for doing this lesson…please
see the next slide…
Credit



I will add 25 points as an assignment grade for you working on
this lesson…
To receive the full 25 points you must do the following:

Have your name, date and period as well a lesson number as a
heading.

Do each of the your turn problems showing all work

Have a 1 paragraph summary of the lesson in your own words
Please be advised – I will not give any credit for work
submitted:

Without a complete heading

Without showing work for the your turn problems

Without a summary in your own words…