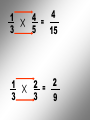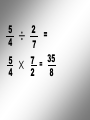Download Operations with Rational Expressions

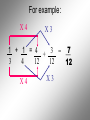
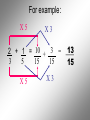
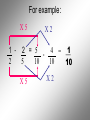
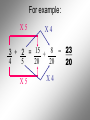
Operations with
Rational Numbers
Any number that can be written in
the form
, where m and n
are integers and n  0, is called a
rational number
In other words, fractions….
Fractions are used when we need
to identify part of a whole.
To combine Rational Numbers, you
must have a …
COMMON DENOMINATOR
• The LCD is the smallest number that
all the denominators divide into
evenly.
Think of the LCD for the following pairs
of numbers
2 and 3
LCD = 6
3 and 4
LCD = 12
2 and 7
LCD = 14
3 and 6
LCD = 6
For example:
X4
X3
1 + 1 = 4
7
3
=
+
3
4
12
12
12
X4
X3
For example:
X5
X3
2 + 1 = 10 + 3 =
3
5
15
15
X5
X3
13
15
For example:
X5
X2
1 - 2 = 5 - 4 = 1
2
5
10
10
10
X5
X2
For example:
X5
X4
3 + 2 = 15 + 8 = 23
4
5
20
20
20
X5
X4
Multiplying and Dividing
Rational Numbers
To multiply Rational Numbers,
multiply corresponding
numerators and denominators
For example:
3
5

4 = 12
7
35
1
3

4 = 4
5
15
1
3

2 =
3
2
9
For division:
Flip the second RN and Multiply
5
7
5
7


2
3
= ?
3 = 15
14
2
5
4
5
4


2 =
7
7 = 35
2
8
See
Sheets