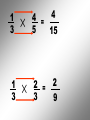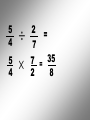* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Operations with Rational Expressions
Foundations of mathematics wikipedia , lookup
Infinitesimal wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Positional notation wikipedia , lookup
Large numbers wikipedia , lookup
System of polynomial equations wikipedia , lookup
Location arithmetic wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
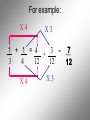
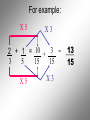
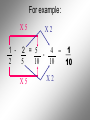
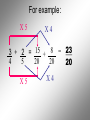
Operations with Rational Numbers Any number that can be written in the form , where m and n are integers and n 0, is called a rational number In other words, fractions…. Fractions are used when we need to identify part of a whole. To combine Rational Numbers, you must have a … COMMON DENOMINATOR • The LCD is the smallest number that all the denominators divide into evenly. Think of the LCD for the following pairs of numbers 2 and 3 LCD = 6 3 and 4 LCD = 12 2 and 7 LCD = 14 3 and 6 LCD = 6 For example: X4 X3 1 + 1 = 4 7 3 = + 3 4 12 12 12 X4 X3 For example: X5 X3 2 + 1 = 10 + 3 = 3 5 15 15 X5 X3 13 15 For example: X5 X2 1 - 2 = 5 - 4 = 1 2 5 10 10 10 X5 X2 For example: X5 X4 3 + 2 = 15 + 8 = 23 4 5 20 20 20 X5 X4 Multiplying and Dividing Rational Numbers To multiply Rational Numbers, multiply corresponding numerators and denominators For example: 3 5 4 = 12 7 35 1 3 4 = 4 5 15 1 3 2 = 3 2 9 For division: Flip the second RN and Multiply 5 7 5 7 2 3 = ? 3 = 15 14 2 5 4 5 4 2 = 7 7 = 35 2 8 See Sheets