Download Slides - Department of Computer Science • NJIT

Lecture 1
BNFO 601
Usman Roshan
Course overview
• Perl progamming language (and some Unix
basics)
– Unix basics
– Intro Perl exercises
– Dynamic programming and Viterbi algorithm in Perl
• Sequence analysis
–
–
–
–
Algorithms for exact and heuristic pairwise alignment
Hidden Markov models
BLAST
Program parameter training for alignment
• Population structure identification using
genome-wide SNP data (time permitting)
Overview (contd)
• Grade: 50% mid-term and 50% final exam
• Exams will cover Perl and bioinformatics
algorithms
• Recommended Texts:
– Introduction to Bioinformatics Algorithms by Pavel
Pevzner
– Biological sequence analysis by Durbin et. al.
– Introduction to Bioinformatics by Arthur Lesk
– Beginning Perl for Bioinformatics by James Tisdall
Nothing in biology makes sense,
except in the light of evolution
-3 mil yrs
AAGACTT
AAGACTT
AAGGCTT
AAGGCTT
_GGGCTT
_GGGCTT
GGCTT
_G_GCTT
(Mouse)
(Mouse)
TAGACCTT
TAGACCTT
TAGGCCTT
TAGGCCTT
(Human)
(Human)
-2 mil yrs
T_GACTT
T_GACTT
TAGCCCTTA
TAGCCCTTA
(Monkey)
(Monkey)
A_CACTT
A_CACTT
ACACTTC
A_CACTTC
(Lion)
ACCTT
A_C_CTT
(Cat)
(Cat)
-1 mil yrs
today
Representing DNA in a format
manipulatable by computers
• DNA is a double-helix molecule made
up of four nucleotides:
–
–
–
–
Adenosine (A)
Cytosine (C)
Thymine (T)
Guanine (G)
• Since A (adenosine) always pairs with
T (thymine) and C (cytosine) always
pairs with G (guanine) knowing only
one side of the ladder is enough
• We represent DNA as a sequence of
letters where each letter could be
A,C,G, or T.
• For example, for the helix shown here
we would represent this as CAGT.
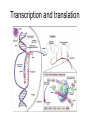
Transcription and translation
Amino acids
Proteins are chains of
amino acids. There are
twenty different amino
acids that chain in
different ways to form
different proteins.
For example,
FLLVALCCRFGH
(this is how we could store
it in a file)
This sequence of amino
acids folds to form a 3-D
structure
Protein folding
Protein folding
• The protein folding
problem is to determine
the 3-D protein structure
from the sequence.
• Experimental techniques
are very expensive.
• Computational are cheap
but difficult to solve.
• By comparing sequences
we can deduce the
evolutionary conserved
portions which are also
functional (most of the time).
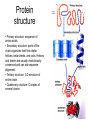
Protein
structure
• Primary structure: sequence of
amino acids.
• Secondary structure: parts of the
chain organizes itself into alpha
helices, beta sheets, and coils. Helices
and sheets are usually evolutionarily
conserved and can aid sequence
alignment.
• Tertiary structure: 3-D structure of
entire chain
• Quaternary structure: Complex of
several chains
Key points
• DNA can be represented as strings
consisting of four letters: A, C, G, and T.
They could be very long, e.g. thousands
and even millions of letters
• Proteins are also represented as strings
of 20 letters (each letter is an amino acid).
Their 3-D structure determines the
function to a large extent.
Pairwise sequence alignment
• How to align two sequences?
Pairwise alignment
• How to align two sequences?
• We use dynamic programming
• Treat DNA sequences as strings over the
alphabet {A, C, G, T}
Pairwise alignment
Dynamic programming
Define V(i,j) to be the optimal pairwise alignment
score between S1..i and T1..j (|S|=m, |T|=n)
Dynamic programming
Define V(i,j) to be the optimal pairwise alignment
score between S1..i and T1..j (|S|=m, |T|=n)
Time and space complexity is O(mn)
How do we understand this dynamic
programming algorithm?
• Let’s first look at some example
alignments
• Let’s look at gaps. How do we know where
to insert gaps
• Let’s look at the structure of an optimal
alignment of two sequences x and y and
how it relates optimal alignments of
subsequences of x and y
Dynamic programming
Animation slides by Elizabeth Thomas in
Cold Spring Harbor Labs (CSHL)
http://meetings.cshl.org/tgac/tgac/flash/DynamicProgramming.swf
How do we pick gap
parameters?
Structural alignments
• Recall that proteins have 3-D structure.
Structural alignment - example
1
Alignment of thioredoxins from
human and fly taken from the
Wikipedia website. This protein
is found in nearly all organisms
and is essential for mammals.
PDB ids are 3TRX and 1XWC.
Structural alignment - example
2
Taken from http://bioinfo3d.cs.tau.ac.il/Align/FlexProt/flexprot.html
Unaligned proteins.
2bbm and 1top are
proteins from fly and
chicken respectively.
Computer generated
aligned proteins
Structural alignments
• We can produce high quality manual
alignments by hand if the structure is
available.
• These alignments can then serve as a
benchmark to train gap parameters so that
the alignment program produces correct
alignments.
Benchmark alignments
• Protein alignment benchmarks
– BAliBASE, SABMARK, PREFAB,
HOMSTRAD are frequently used in studies for
protein alignment.
– Proteins benchmarks are generally large and
have been in the research community for
sometime now.
– BAliBASE 3.0
Biologically realistic scoring matrices
• PAM and BLOSUM are most popular
• PAM was developed by Margaret Dayhoff
and co-workers in 1978 by examining
1572 mutations between 71 families of
closely related proteins
• BLOSUM is more recent and computed
from blocks of sequences with sufficient
similarity
PAM
• We need to compute the probability transition
matrix M which defines the probability of amino
acid i converting to j
• Examine a set of closely related sequences
which are easy to align---for PAM 1572
mutations between 71 families
• Compute probabilities of change and
background probabilities by simple counting
Next week
• Basics of Unix
• Perl programming
– Basics
– Exercises
– Dynamic programming alignment solution in
Perl