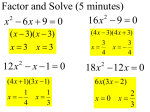Download CH2_4_ Complex numbers LESSON NOTES

Section 2.4: Imaginary Unit and Complex Numbers
Imaginary Unit:
Some polynomial equations have complex (non-real) solutions, when a negative number is under the
radical symbol. For example,
16 or 36 .
there is no real solution to
Mathematicians (for fun, maybe?!) created a new system of numbers using the imaginary unit, i, defined
as i  1 . With this new system of numbers, radicals of negative numbers can now be simplified!
Therefore;
 16  (1)(16)  16   1  4i
 36  (1)(36)  36   1  6i
 27  (1)(9)(3)  9   1  3  3i 3 or 3 3i where ‘i’ is NOT under the radical sign!
 20  (1)(20)  20   1  i 20 or

i2 
i3 
i4  1
2
 1  1

i4 

i3  i
i 2  1
i  1
20 i where ‘i’ is NOT under the radical sign!
 
3
1 
1


2
 1  1  i  i
  1    1   1
4
2
2
 1  1  1
Definition of Complex Numbers:
A complex number z is a number of the form
z=a+bi
where a and b are real numbers and i is the imaginary unit defined by
a is called the real part of z and b is the imaginary part of z.
Operations on Complex Numbers:
Addition and Subtraction is similar to grouping like terms where real parts are combined with
real parts and imaginary parts are combined with imaginary parts.
Example:
Express in the form of a complex number a + b i.

(2 + 3i) + (-4 + 5i) =
(2 - 4) + (3i + 5i)
=real
imaginary
2 + 8i
(-2 is the real part of this complex number, 8i is the
imaginary part)
EXAMPLES:
1] (3i) + (-5 + 6i) = -5 +9i
2] (2) + (-2 + 9i) = 0 + 9i = 9i
3] (2 - 5i) - (-4 - 5i) = 6 +0i = 6
Multiplication of Complex Numbers
The multiplication of two complex numbers is performed using properties similar to those of the real
numbers (FOIL) and distributive property. Remember that
Simplify each expression and express in the form of a complex number a + bi.
EXAMPLE 1.:
5(2 + 7i) = 10 + 35i
EXAMPLE 2.:
(6 − i)(5i) = 30i – 5i2 = 5 + 30i
EXAMPLE 3:
(2 − i)(3 + i) = 6 +2i – 3i - i² = 6 – i – (-1) = 7 – i
EXAMPLE 4:
(5 + 3i)²= 25 +30i + 9i² = 25 +30i +9(– 1) = 16 + 30i
Division of Complex Numbers
Earlier, in Geometry and Adv Algebra we learned how to rationalize the denominator of an expression
like the expression below. We multiplied numerator and denominator by the “conjugate” of the
denominator, 3 + √2:
EXPRESS
3 j
42j
The conjugate of 4 − 2j is 4 + 2j.

TRY TO SIMPLIFY:
8  4i
1 i
8  4i 1  i 8  8i  4i  4i 2



1 i 1 i
1 i  i  i2
Answer:
8  12i  4(1) 4  12i

 2  6i
1  (1)
2
7 1

j
10 10
PRACTICE QUIZ :
1.
5.
Simplify each radical using imaginary numbers.
16
2.
 16   2
7
3.
27
7. i 5
6. i³
54
4.
8. i 6
Simplify and write final answer in standard form (a +bi).
1. (3  i)  (2  3i)
2. 2i  (4  2i)
3. 3  (2  3i)  (5  i )
4. (3  2i)  (4  i)  (7  i)
5.
7. (3  2i)(3  2i)
8. 4i(1  5i)
6. (2  i)(4  3i)
4  16
2
9. (3  2i )
Write the following quotients in standard form.
1.
2  3i
4  2i
2.
2i
2i
3.
i
(4  5i ) 2
4.
54
ANSWER KEY :
Simplify each radical using imaginary numbers.
1. 16
=
4i
2.
7 = i 7
3.
27
3i 3
i³  i
5.  16   2
6.
4i  i 2  4i 2 2 =  4 2
Simplify and write final answer in standard form (a +bi).
(3  i)  (2  3i)
2.
5  2i
4. (3  2i)  (4  i)  (7  i)
7. (3  2i)(3  2i)
0
13
2. 2i  (4  2i)  4
5.
4  16
8. 4i(1  5i)
8
 20  4i
7. i 5
3i 6
i
8. i 6
1
3. 3  (2  3i)  (5  i)
 2i
6. (2  i)(4  3i) 11 2i
2
9. (3  2i ) 5  12i
Write the following quotients in standard form.
2.
2  3i
4  2i
2  16i 1 4i
 
20
10 5
2.
2i
2i
3 4i

5 5
3.
i
(4  5i ) 2
 40
9i

1681 1681