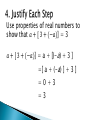* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Properties of Real Numbers
Large numbers wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Infinitesimal wikipedia , lookup
Surreal number wikipedia , lookup
Hyperreal number wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
P-adic number wikipedia , lookup
Real number wikipedia , lookup
Division by zero wikipedia , lookup
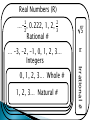
Turn in syllabus return slip (pass up) ◦ Due today or tomorrow Take out last night’s hw ◦ Stamp Take out piece of paper ◦ Fold in half (Warm up & Ticket out the door) ◦ For WARM UP (Do it soooooon!) The graph shows the cost of bowling for one person. a. Make a table. b. How much does 8 games cost for one person? c. What is the total cost if 4 people each bowl 4 games? EXPLAIN! # of Games 1 Process 3(1) Cost per person $3 2 3(2) $6 3 3(3) $9 ∶ ∶ ∶ 8 3(8) $24 n 3(n) $3n b. Each game costs $3 for one period. It costs $24 for one person to play 8 games. c. Each game costs $3 per person. So it costs $12 for one person to play 4 games. Therefore, it will cost $48 total for 4 people to play 4 games each. Algebra II To To graph & order real numbers identify properties of real numbers Use natural numbers to count 1, 2, 3, … NO ZERO!!! Natural numbers & zero 0, 1, 2, 3, … Include ZERO, think w“hole” Natural numbers, their opposites, and zero …–3, –2, –1, 0, 1, 2, 3, … Numbers you can write as a quotient of integers (fractions) 5 3 1 4 Decimals terminate (end) 0.5 Decimals 1. 3 1.75 repeat 1.16 Decimals do not repeat nor end 2 ≈ 1.414213 … . 𝜋 Cannot be written as a fraction Real Numbers (R) 1 …- , 2 0.222, 1, 2, Rational # 2 3 … –3, –2, –1, 0, 1, 2, 3… Integers 1, 2, 3… Natural # 𝜋 Irrational # 0, 1, 2, 3… Whole # 5 9=3 R, Q, Z, W, N R, Q 7 9 – 7 R, Q, Z 7 ≈ 2.6457 … R, I 9 < 3.8 10 > 3.1 28 9 < 3.2 24 4 > 𝜋 10 ≈ 3.162 … 28 9 = 3.1 Opposite – aka additive inverse, of any number a is –a . 12 & –12 –7 & 7 Reciprocal – aka multiplicative inverse, of any nonzero number a is 1 . 𝑎 8 & 1 8 5& 1 − 5 Addition Multiplication a +b is a real # ab is a real # a +b=b+a ab = ba (a+b)+c=a+(b+c) (ab)c = a(bc) Addition a+0=a 0 + a = a 0 is the additive identity a + (–a) = 0 Multiplication a ∙1= a 1 ∙ 𝑎= a 1 is the multiplicative identity a ∙ 1 𝑎 =1, a≠ 0 Addition Multiplication 3 ∙ 4 ∙ 5 = 4 ∙ 3 ∙ 5 Commutative Prop of Mult. 2 − 3 3(x 3 − 2 =1 Inverse Prop of Mult. + y) + 2x = (3x + 3y) +2x Distributive Prop Use properties of real numbers to show that 𝑎 + [ 3 + (−𝑎)] = 3 𝑎 + [ 3 + (−𝑎)] = a + [(-a) + 3 ] =[ a + (-a) ] + 3 ] =0+3 =3 𝑎 + [ 3 + (−𝑎)] = a + [(-a) + 3 ] Commutative Prop of Add. =[ a + (-a) ] + 3 ] Associative Prop of Add. =0+3 Inverse Property of Addition =3 Identity Property of Addition Are there two integers with a product of –12 and a sum of –3? Explain.