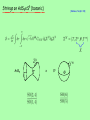* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 20071031110012301
Identical particles wikipedia , lookup
Quantum entanglement wikipedia , lookup
Quantum potential wikipedia , lookup
Uncertainty principle wikipedia , lookup
Bell's theorem wikipedia , lookup
Double-slit experiment wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Grand Unified Theory wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Quantum state wikipedia , lookup
Supersymmetry wikipedia , lookup
Feynman diagram wikipedia , lookup
Quantum field theory wikipedia , lookup
Standard Model wikipedia , lookup
Path integral formulation wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Renormalization group wikipedia , lookup
Quantum logic wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Old quantum theory wikipedia , lookup
Relational approach to quantum physics wikipedia , lookup
Monte Carlo methods for electron transport wikipedia , lookup
Electron scattering wikipedia , lookup
String theory wikipedia , lookup
Quantum gravity wikipedia , lookup
Quantum chaos wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Canonical quantization wikipedia , lookup
Canonical quantum gravity wikipedia , lookup
Elementary particle wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Renormalization wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
Event symmetry wikipedia , lookup
Scalar field theory wikipedia , lookup
History of quantum field theory wikipedia , lookup
Theory of everything wikipedia , lookup
Yang–Mills theory wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Topological string theory wikipedia , lookup
INI Cambridge, 31.10.2007 Quantum Integrability of AdS String Theory: Factorized Scattering in the near-flat limit Thomas Klose Princeton Center for Theoretical Physics based on work with Valentina Giangreco Puletti and Olof Ohlson Sax: hep-th/0707.2082 also thanks to T. McLoughlin, J. Minahan, R. Roiban, K. Zarembo for further collaborations Quantum Integrability of AdS String Theory: Factorized Scattering in the near-flat limit String waves in flat space ►Simple Fock spectrum Quantum Integrability of AdS String Theory: Factorized Scattering in the near-flat limit String waves in curved space ? ? ►Spectrum unknown Quantum Integrability of AdS String Theory: Factorized Scattering in the near-flat limit String waves in AdS5 x S5 ►Spectrum from Bethe eq‘s Talk overview AdS/CFT Spectrum Proposed Bethe equations Previous checks of integrability Intro Integrability and Scattering Conserved charges No particle production Factorization Superstrings on AdS5 x S5 World-sheet scattering and S-matrix Near-flat-space limit ► Factorization of three-particle world-sheet S-matrix in near-flat AdS5 x S5 to one loop in string σ-model = = (163)2 compoments, but only 4 independent ones ! AdS/CFT spectrum Conformal dimensions String energies Emergence of integrable structures ! IIB Strings on SYM on Spectrum of string energies ► Dispersion relation (propagation of excitation) dispersionless non-relativistic lattice relativistic AdS/CFT ► Momentum selection (periodicity+level matching) Phase shift Spectrum of string energies ► If String theory was integrable... ... then the multi-particle phase shifts would be products of ... and the momenta would satisfy Bethe equations like ... and the spectrum would be given by Proposed Bethe equations for AdS/CFT Nested Bethe equations Bethe roots [Beisert, Staudacher ‘05] Rapidity map Dressing phase [Beisert, Eden, Staudacher ‘07] Dispersion relations [Dorey, Hofman, Maldacena ’07] planar asymptotic spectrum Brief history of the dressing phase Dressing phase [BHL ‘06] SYM side String side [HL ‘06] [BES ‘06] [AFS ‘04] [BDS ‘04] “trivial” 0 1 2 3 4 2 1 0 Checks in 4-loop gauge theory Checks in 2-loop string theory [Bern, Czakon, Dixon, Kosower, Smirnov ‘06] Tristan’s talk tomorrow [Beisert, McLoughlin, Roiban ‘07] Checks of Integrability in AdS/CFT ► Integrability of planar N=4 SYM theory [Minahan, Zarembo ‘02] Spin chain picture at large N Dilatation operator Hamiltonian of integrable spin-chain Algebratic Bethe ansatz at 1-loop Degeneracies in the spectrum at higher loops Inozemtsev spin chain up to 3-loops in SU(2) sector Factorization of 3-impurity S-matrix in SL(2) sector [Minahan, Zarembo ‘02] [Beisert, Staudacher ‘03] [Beisert, Kristjansen, Staudacher ‘03] [Serban, Staudacher ‘04] [Eden, Staudacher ‘06] Checks of Integrability in AdS/CFT ► Classical Integrability of planar AdS string theory [Mandal, Suryanarayana, Wadia ‘02] [Bena, Polchinski, Roiban ‘03] Coset representative Current conserved flat Family of flat currents Monodromy matrix generates conserved charges Checks of Integrability in AdS/CFT ► Quantum Integrability of planar AdS string theory Quantum consistency of AdS strings, and existence of higher charges [Berkovits ‘05] in pure spinor formulation Check energies of multi-excitation states against Bethe equations [Callan, McLoughlin, Swanson ‘04] (at tree-level) [Hentschel, Plefka, Sundin ‘07] Absence of particle production in bosonic sector in semiclassical limit [TK, McLoughlin, Roiban, Zarembo ‘06] Quantum consistency of monodromy matrix [Mikhailov, Schäfer-Nameki ‘07] Integrability in 1+1d QFTs Existence of local higher rank conserved charges ► No particle production or annihilation [Shankar, Witten ‘78] [Zamolodchikov, Zamolodchikov ‘79] [Parke ‘80] ► Conservation of the set of momenta ► -particle S-Matrix factorizes into 2-particle S-Matrices Conservation laws and Scattering in 1+1 dimensions ► 1 particle ► 2 particles ► 3 particles ► particle Conservation laws and Scattering in 1+1 dimensions local conserved charges [Parke ‘80] with action conservation implies: “Two mutually commuting local charges of other rank than scalar and tensor are sufficient for S-matrix factorization !” Strings on AdS5xS5 (bosonic) AdS5 [Metsaev, Tseytlin ‘98] x S5 Strings on AdS5xS5 (bosonic) ► Fixing reparametization invariance in uniform lightcone gauge [Arutyunov, Frolov, Zamaklar ‘06] worldsheet Hamiltonian density eliminated by Virasoro constraints ► Back to Lagrangian formulation Strings on AdS5xS5 (bosonic) ► Decompactification limit rescale such that world-sheet size no , no loop counting parameter send to define asymptotic states Superstrings on AdS5xS5 [Metsaev, Tseytlin ‘98] ► Sigma model on Gauge fixing (L.C. + -symmetry) [Frolov, Plefka, Zamaklar ‘06] Manifest symmetries Worldsheet S-Matrix ► 4 types of particles, 48=65536 Matrix elements ► Group factorization ► Each factor has manifest invariance Symmetry constraints on the S-Matrix In infinite volume, the symmetry algebra gets centrally extended to [Beisert ‘06] ► 2-particle S-Matrix: for one S-Matrix factor: irrep of of centrally extended algreba relate the two irreps of the total S-Matrix is: fixed up to one function Symmetry constraints on the S-Matrix ► 3-particle S-matrix: fixed up to four functions 3-particle S-matrix ► Eigenstates Extract coefficient functions from: ► Disconnected piece: factorizes trivially, 2-particle S-matrix checked to 2-loops [TK, McLoughlin, Minahan, Zarembo ‘07] ► Connected piece: factorization at 1-loop to be shown below ! Near-flat-space limit ► Boost in the world-sheet theory: Highly interacting giant magnons [Hofman, Maldacena ‘06] Only quartic interactions ! near-flat-space plane-wave Free massive theory [Maldacena, Swanson ‘06] [Berenstein, Maldacena, Nastase ‘02] Near-flat-space limit Coupling constant: Propagators: bosons , fermions ! Non-Lorentz invariant interactions ! Decoupling of right-movers ! UV-finiteness ! quantum mechanically consistent reduction at least to two-loops Tristan’s talk tomorrow 2-particle S-Matrix in Near-Flat-Space limit Overall phase: Exact coefficients for one PSU(2|2) factor: S-Matrix from Feynman diagrams ► 2-particle S-matrix ► 4-point amplitude compare for S-Matrix from Feynman diagrams ► 3-particle S-matrix ► 6-point amplitude !? Factorization !? Factorization YBE Emergence of factorization light-cone momenta ► Tree-level amplitudes compare to sinh-Gordon: sets the internal propagator on-shell Emergence of factorization ► Example from Feynman diagrams ... agrees with the predicted factorized 3-particle S-Matrix disconnected Emergence of factorization ► 1-loop amplitudes “dog”: “sun”: phase space Emergence of factorization Cutting rule in 2d for arbitrary 1-loop diagrams [Källén, Toll ‘64] Applied to “sun-diagram”: Emergence of factorization The below identification... ► General 3-particle S-Matrix works for symmetric processes like fails for mixed processes like cannot hold at higher loops, e.g. ► Contributions at order 2-loop 2-particle S-Matrix “dog structure” “sun structure” Summary and open questions ! Proven the factorization of the 3-particle world-sheet S-Matrix to 1-loop in near-flat AdS5xS5 effectively ! 1-loop computation of the highest-weight amplitudes, amplitude of mixed processes fixes 3-particle S-matrix checks supersymmetries ! Direct check of quantum integrability of AdS string theory (albeit in the NFS limit) ? Extenstions of the above: higher loops, more particles, full theory ? Finite size corrections Asymptotic states?