* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download ppt
Genomic imprinting wikipedia , lookup
Population genetics wikipedia , lookup
Microevolution wikipedia , lookup
Public health genomics wikipedia , lookup
History of genetic engineering wikipedia , lookup
Gene expression programming wikipedia , lookup
Behavioural genetics wikipedia , lookup
Species distribution wikipedia , lookup
Human genetic variation wikipedia , lookup
Designer baby wikipedia , lookup
Pharmacogenomics wikipedia , lookup
Dominance (genetics) wikipedia , lookup
Genome (book) wikipedia , lookup
Biology and consumer behaviour wikipedia , lookup
Genome-wide association study wikipedia , lookup
Heritability of IQ wikipedia , lookup
Site-specific recombinase technology wikipedia , lookup
QTL mapping in mice
Lecture 10, Statistics 246
February 24, 2004
1
The mouse as a model
Same genes?
The genes involved in a phenotype in the mouse may also be
involved in similar phenotypes in the human.
Similar complexity?
The complexity of the etiology underlying a mouse phenotype
provides some indication of the complexity of similar human
phenotypes.
Transfer of statistical methods.
The statistical methods developed for gene mapping in the
mouse serve as a basis for similar methods applicable in
direct human studies.
2
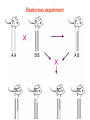
Backcross experiment
3
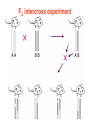
F2 intercross experiment
4
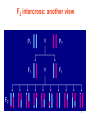
F2 intercross: another view
5
Quantitative traits (phenotypes)
133 females from our earlier (NOD B6) (NOD B6) cross
Trait 4 is the log count of a particular white blood cell type.
6
Another representation of a trait distribution
7
Note the equivalent of dominance in our trait distributions.
A second example
8
Note the approximate additivity in our trait distributions here.
Trait distributions:
a classical view
In general we seek a difference
in the phenotype distributions
of the parental strains before we
think seeking genes associated
with a trait is worthwhile.
But even if there is little difference,
there may be many such genes.
Our trait 4 is a case like this.
9
Data and goals
Data
Phenotypes: yi = trait value for mouse i
Genotype:
xij = 1/0 of mouse i is A/H at marker j (backcross);
need two dummy variables for intercross
Genetic map: Locations of markers
Goals
•Identify the (or at least one) genomic region, called quantitative
trait locus = QTL, that contributes to variation in the trait
•Form confidence intervals for the QTL location
•Estimate QTL effects
10
Genetic map from our NOD B6 intercross
11
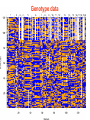
Genotype data
12
Models: Recombination
We assume no chromatid or crossover interference.
points of exchange (crossovers) along
chromosomes are distributed as a Poisson process,
rate 1 in genetic distancce
the marker genotypes {xij} form a Markov chain
along the chromosome for a backcross;
what do they form in an F2 intercross?
13
Models: GenotypePhenotype
Let y = phenotype,
g = whole genome genotype
Imagine a small number of QTL with genotypes
g1,…., gp (2p or 3p distinct genotypes for BC, IC
resp).
We assume
E(y|g) = (g1,…gp ), var(y|g) = 2(g1,…gp)
14
Models: GenotypePhenotype, ctd
Homoscedacity (constant variance)
2(g1,…gp) = 2 (constant)
Normality of residual variation
y|g ~ N(g ,2 )
Additivity:
(g1,…gp ) = + ∑j gj (gj = 0/1 for BC)
Epistasis: Any deviations from additivity.
15
Additivity, or non-additivity (BC)
16
Additivity or non-additivity: F2
17
The simplest method: ANOVA
•Split mice into groups
according to genotype
at a marker
•Do a t-test/ANOVA
•Repeat for each marker
•Adjust for multiplicity
LOD score = log10 likelihood ratio, comparing single-QTL 18
model to the “no QTL anywhere” model.
Exercise
1.
Explain what happens when one compares trait
values of individuals with the A and H genotypes in
a backcross (a standard 2-sample comparison),
when a QTL contributing to the trait is located at a
map distance d (and recombination fraction r) away
from the marker.
2. Can the location of a QTL as in 1 be estimated,
along with the magnitude of the difference of the
means for the two genotypes at the QTL? Explain
fully.
19
Interval mapping (IM)
Lander & Botstein (1989)
• Take account of missing genotype data (uses the HMM)
• Interpolates between markers
• Maximum likelihood under a mixture model
20
Interval mapping, cont
Imagine that there is a single QTL, at position z between two
(flanking) markers
Let qi = genotype of mouse i at the QTL, and assume
yi | qi ~ Normal( qi , 2 )
We won’t know qi, but we can calculate
pig = Pr(qi = g | marker data)
Then, yi, given the marker data, follows a mixture of normal
distributions, with known mixing proportions (the pig).
Use an EM algorithm to get MLEs of = (A, H, B, ).
Measure the evidence for a QTL via the LOD score, which is the
log10 likelihood ratio comparing the hypothesis of a single QTL
at position z to the hypothesis of no QTL anywhere.
21
Exercises
1.
2.
Suppose that two markers Ml and Mr are separated by map distance
d, and that the locus z is a distance dl from Ml and dr from Mr.
a) Derive the relationship between the three recombination fractions
connecting Ml , Mr and z corresponding to dl + dr = d.
b) Calculate the (conditional) probabilities pig defined on the previous
page for a BC (two g, four combinations of flanking genotypes), and
an F2 (three g, nine combinations of flanking genotype).
Outline the mixture model appropriate for the BC distribution of a QT
governed by a single QTL at the locus z as in 1 above.
22
LOD score curves
23
LOD curves for Chr 9 and 11 for trait4
24
LOD thresholds
To account for the genome-wide search, compare the observed
LOD scores to the distribution of the maximum LOD score,
genome-wide, that would be obtained if there were no QTL
anywhere.
LOD threshold = 95th %ile of the distribution of genome-wide
maxLOD,, when there are no QTL anywhere
Derivations:
• Analytical calculations (Lander & Botstein, 1989)
• Simulations
• Permutation tests (Churchill & Doerge, 1994).
25
Permutation distribution for trait4
26
Epistasis for trait4
27
Acknowledgement
Karl Broman, Johns Hopkins
28