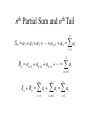* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Section 11.2: Series
History of Grandi's series wikipedia , lookup
Large numbers wikipedia , lookup
Infinitesimal wikipedia , lookup
Uniform convergence wikipedia , lookup
Real number wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Collatz conjecture wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
Central limit theorem wikipedia , lookup
Hyperreal number wikipedia , lookup
Section 11.2:
Series
Infinite Series of Real Numbers
1. Sequence of terms:
a1 , a2 , a3 ,
2. Sequence of partial sums:
S1 , S 2 , S3 ,,
3. Series:
a
i 1
i
n
where S n ai
a1 a2 a3
i 1
th
n
Partial Sum and
th
n
Tail
n
S n a1 a2 a3 an 1 an ai
i 1
Rn an 1 an 2 an 3
n
S n Rn ai
i 1
a
i n 1
a a
i n 1
i
i 1
i
i
Convergence of a Series
If lim S n S for some finite number S, then the
n
series
a converges to the limit S. Otherwise,
i 1 i
the series diverges.
The Divergence Test
• If the sequence {an} does not converge to 0,
then the series
diverges.
a
n
n 1
The Harmonic Series
1
1 1
1
1
2 3
n
n 1 n
Geometric Series
•
n 1
2
n 1
ar
a
ar
ar
ar
n 1
• Convergence
a
.
– If r 1, converges to
1 r
– If r 1, diverges .
Algebra with Series
a b a b
i 1
i
i
i 1
ca
i 1
i
i
c ai
i 1
i 1
i