Download Forces Fundamental interactions in particle physics

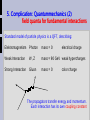
Forces
Fundamental interactions in particle physics
U. Straumann, Aarau, 25.3.06
Forces and fundamental interactions
Contents:
1. Gravitation and Electrostatics
2. Electrodynamics: Electric and Magnetic united
3. More forces: weak and strong
4. Principle of the scattering experiment
5. Quantummechanical complications
6. Example experiment
7. Grand unification?
Summary and outlook
U. Straumann, Aarau, 25.3.06
1. Gravitation and Electrostatics (1)
Newton and Coulomb
Newton's law:
Force of gravitation between two bodies 1 and 2:
m1⋅m2
F =⋅ 2
R
Coulomb's law:
Electrical force between two bodies 1 and 2, carrying
electric charge qi
1 q 1⋅q 2
F=
⋅ 2
4 0 R
Same formula, but two different constants!
1. Gravitation and Electrostatics (2):
2 – particles bound states:
Earth – Moon:
m 1⋅m2
E pot =−⋅
R
R
Hydrogen atom: Proton – Electron
same drawing, same formula,
different constants (and QM, see later)
p
+
e-
1. Gravitation and Electrostatics (3):
comparison in more detail:
Strength: Compare electrostatic and gravitation force of two
bodies with mass mP and unity electrical charge e:
They are equal, if
=>
m P⋅m P
1 e⋅e
⋅
=
⋅ 2
2
4 0 R
R
(Planck mass)
m P =21.77  g
electrical charge exists only in whole numbers of e
E: attractive or repulsive, G: always attractive (incl. antimatter)
G: mT=mS mass of inertia = mass of gravity, thus all bodies
feel the same acceleration (Galilei's law of free fall).
2. Electrodynamics (1):
magnetostatic forces:
Experimental evidence very old
complicate laws:
proportional to R3 ,also torque
2. Electrodynamics (2):
unification of electr. and magn. forces:
by Faraday and Maxwell in 19th century
Magnetic fields are created by moving electrical charges
or time – varying electrical fields
Time – varying magnetic fields
generate electrical fields
A set of 4 equations (Maxwell equations)
describe all electromagnetic effects consistently.
Electric and magnetic forces are two different phenomena
which have their origin in the same physics law
There is only one fundamental constant: c
2. Electrodynamics (3):
explains new effects:
Maxwell's equations explain also
electromagnetic waves, for instance light.
Speed of light is constant = c,
independent of speed of source
or speed of observer
=> theory of special relativity (Einstein 1905)
Maxwell's electrodynamics is probably the best theory we have:
it truely unifies two forces
it explains additional effects, like light
it predicts correctly the theory of special relativity.
3. More interactions: weak and strong force(1):
What is the proton made of?
Protons and Neutrons are made of three quarks each.
u quark: q=2/3 e
d quark: q=-1/3 e
proton: uud
neutron: udd
q=+1
q=0
Epot
The forces between the quarks
are due to the strong interaction
The “charges” on which the strong
force interacts are called “colors”:
There are three colors: red green blue.
-> Quantum chromo dynamics, QCD.
s
p
e
e
-> k
!
g
n
i
ris
R
3. More interactions: weak and strong force(2):
What makes the sun shining?
There are many processes, most importantly:
Protons (Hydrogen) are melt together to form He-4.
He-4 nucleus = ppnn
need to change
some p into n.
u quark into d quark
ν
d
e
u
= weak interaction
(“β rays”)
3. More interactions: weak and strong force(3):
Properties of weak interaction
The weak interaction is also responsible for β radioactivity.
It has a very short range:
1 − R
E pot ~ − e
R
with μ = 1/0.002 fm
The only interaction with this
short range.
At very small R same formula as the
other interactions, but different const.
Epot
R
3. More interactions (4):
Four fundamental interactions
As of today, we know four fundamental interactions:
“classical” description:
Gravity
infinite range
Electric
infinite range
Strong
confinement
Weak
short range
Each of them has its own
interaction constant.
Do they become similar at small R?
Epot
R
4. How to measure ? The scattering experiment:
Conceptual idea
Basic setup:
Beam energy determines
Rmin, i.e. the resolution
Target object
Particle Detector
θ
particle beam
Rmin
Measure probability of scattered particle
as a function of:
- energy
- scattering angle θ
(often colliding beams are used)
4. The scattering experiment(2):
Determine interaction law
Example 1: “hard ball”
interaction at surface
for instance neutrons.
Example 2: Electrically
charged particles, for instance
electron and quark (inside proton)
Probability
Probability
1
sin 4 /2
0º
Epot
↕
180º
θ
0º
Epot
R
↕
180º
1
R
R
θ
4. The scattering experiment(3):
What we can learn in addition:
From overall scattering probability
-> coupling constant
From energy of scattered particle
-> momentum of target particle
Energy of beam particle determines, how close we can come: Rmin
-> “resolution” of experiment
-> need large energy to determine law at small distances
Often additional particles produced
-> more detail about nature of interaction.
5. Complication: Quantummechanics (1)
1. Discrete energy and angular momentum states in bound
systems, for instance Hydrogen atom.
2. Interaction field comes in quanta as well,
“interaction carriers”, “exchange particles”, “propagator”
are also particles.
Example: El-mag. interaction:
Photon
“Quantum field theory” (QFT)
5. Complication: Quantummechanics (2)
field quanta for fundamental interactions
Standard model of particle physics is a QFT, describing:
Elektromagnetism Photon
mass = 0
electrical charge
Weak Interaction
W, Z
mass ≈ 90 GeV weak hypercharges
Strong Interaction
Gluon
mass = 0
color charge
The propagators transfer energy and momentum.
Each interaction has its own coupling constant
6. Example experiment:
electron proton collider at DESY, Hamburg
circumference
6.5 km
electron 29 GeV
proton 920 GeV
collide at two
positions
Experiment H1
p
measure direction
and energy of
all particles
produced
e
Some members of the H1 Collaboration
Work at the innermost parts of the H1 detector
HERA e-p scattering events
observed in the H1Detector
Calorimeter
A NC-DIS event with two jets
gluon
'
ep e Jet 1 Jet 2
Jet2
e
electron
Jet2
e
Jet1
e
quark
Jet1
J1
J2
7 Grand Unification
Coupling constants are not exactly constant:
Coupling Constants
They vary slowly
with energy ( = 1 / Rmin)
Theoretically predicted
str
on
g
weak
Do they meet at
high energy?
= Unified interaction
netic
electromag
Energy, ~1 / Rmin
100 GeV
Todays experiments
1016 GeV
7 Grand Unification:
Experimental result on strong interaction
Strong
Coupling
Constant
Energy, ~1/R
7. Grand Unification:
extrapolation to very high energies
Experimental result:
1 / (Coupling Constants)
Coupling constants do NOT excactly
meet at high energy, but almost.
If they would meet, we would
have unified the interactions!
May be there is new
physics, new interactions?
What about Gravity?
Energy, ~1/R
Summary
Forces and interactions
Long distance (low energy):
Fundamental forces are described by their
potential energy. We know 4 fundamental forces:
Gravity, electromagnetic, strong and weak
Epot
R
Short distance (high energy):
Fundamental interactions are described by
Quantum Field Theory (QFT), with exchange particles.
The standard model (SM) of particle physics
is a QFT describing three different interactions:
Electromagnetic, strong and weak.
Same formalism, but different constants.
Are the three SM forces different, low-energy phenomena of the
same fundamental interaction? Can we unify them at very high enery?
Outlook
From 2008 a new collider (pp) at CERN, called LHC, will
search for new physics and new interactions.
Open questions on fundamental interactions:
- Is there new physics, which would allow to exactly unify
the interactions at high energies?
- “Dark Matter” in the universe asks for new particles and
interaction in the mass region, reachable by LHC
- How to include gravity in a consistent QFT of all interactions?