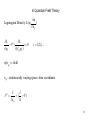Download Euler Lagrange Equation

Lattice Quantum Chromodynamics
By
Leila Joulaeizadeh
19 Oct. 2005
1- Literature : Lattice QCD , C. Davis
Hep-ph/0205181
2- Burcham and Jobes
1
Outline
- Introduction
- Hamilton principle
- Local gauge invariance and QED
- Local gauge invariance and QCD
- Lattice QCD calculations
- Some results
- Conclusion
2
What is Quantum Chromodynamics and why LQCD?
-
Strong interaction between coloured quarks by exchange of coloured gluon
- Gluons carry colour so they have self interaction
- Self interaction of gluons , nonabelian group SU(3)
-
QCD is a nonlinear theory so there is no analytical solution and we should use numerical methods
3
Euler Lagrange Equation
x1
I

x1
f ( y, y ' )dx
for minimising I

I  f ( y, y ' )dx  0
x0
x0
y(x 0 )  y(x1 )  0
x1

x0
y' 
d
y
dx
x1
(
f
f
f
f d
y  ' y ' )dx  ( y  ' ( y))dx
y
y
y
y dx
x

0
U sin g partial integratio n and y(x)  0
f
d f

0
y dx y '
4
For motion of a point like particle with mass m in a central potential:
L
1
m( x 2  y 2  z 2 )  V(r )
2
L
V

 Fx
x
x
L
  mx  Px
x

L d L

0
x dt x
 generaliza tion
t1

Action S  L.dt is minimized
t0
L d L

0

q i dt q i
Hamilton Principle
Physical systems will evolve in such a way to
minimize the action
5
In Quantum Field Theory

Lagrangian Density : L( ,
)
x 
L
L

 (
)0
i
 (   i )
i  1,2,3,...
(x  )  field
x  : continuously varying space - time coordinate
 


 ( , )
x 
t
6
Examples
Scalar field (spin 0 particle)
1
1 2 2 1 
1 2 2

L  (  )(  )  m   g (  )(   )  m 
2
2
2
2
    m2  0
Klein - Gordon Eq.
Spinor field(spin 1/2 particle)
_

_
_

_
L  i       m    i     m   0 Dirac eq.
7
Local Gauge Invariance and QED
Transforma tion parameter  is a function of x :  (x)
   '  exp[ iq  ( x )] ( x )
,
   '  exp[ iq  ( x )] ( x )
For a free Dirac particle of mass m : L  i        m 
After local gauge transformation :
L'  i exp[ iq  ( x )] ( x )     (exp[ iq  ( x )] ( x ))  m exp[ iq  ( x )] ( x ) exp[ iq  ( x )] ( x )
 i        q        m   L
Gauge covariant derivative :
D      iqA  ( x ) , D    exp[ iq  ( x )]D  
,
A  ( x )  A  ( x ) -   ( x )
L  i    D    m   i        m   qA       L free  j A 
j  q    
8
We add kinetic energy term :
L  L free  j A  
1
FFμν
4
If the photon were not massless : L  
F    A     A 
1 2
1
m  A  A   L'   m 2 (A     )( A      )  L 
2
2
Example
Massless vector field(spin 1)
1
L   FF  j A     F  j
4
Covariant form of Maxwell equation
9
Local Gauge Invariance and QCD
 q   ' q  exp[ ig s  a ( x )Ta ] q ( x )
Ta , Tb   if abcTc
,
 q   ' q  exp[ ig s  a ( x )Ta ] ' q ( x )
SU(3) group generators
For a free Dirac particle of mass m : L 
i 
j
q
     qk 
m  
q
q
j
q
j
q
q
After local gauge transformation : L'  L
D      ig s Ta Ba
,
Ba ( x )  Ba ( x ) -    a ( x ) 
g s f abc  b ( x )Bc ( x )
Non-Abelian nature of SU(3)
L  i  q   D   q  m q  q  q  i  q      q  m q  q  q  g s (  q   Ta  q )Ba
We add kinetic term : L 

j
i  q   (D  ) jk  qk 
q
(D  ) jk   jk    ig s (Ta ) jk Ba

q
m q  qj  qj 
1 a 
BBa
4
a  1,2,...,8
b c
a
B
   Ba    Ba  g s f abc B B
Gluon self interaction term
B  D B  D B
10
Diagrams representing propagation of free quark and gluon and their interaction
11
Lattice QCD
O : operator whose expectation value we want to calculate
0O0 
S




d

[
d

]
dA
O
[

,

,
A
]
e


 d[d  ]dA e


After discretisation : d 4 x 

n
S
a
4
,
 (x, t)   (n i a, n t a)
a : spacing between the points
n
Scalar field theory lagrangian L 
Lattice action : S 

S  Ld 4 x
1
1
(  ) 2  m 2  2
2
2
2
4
 (n  1 )  (n  1 ) 
1 2 2
4 1
a (

m  (n ))


2  1 
2a
2


12
Lattice gauge theory for gluons
Gluon field in continuum B b
x
X+1
U (x)
U e
Gluon field in lattice
U ( g ) ( x )
ikgB
 G ( x ) U  ( x )G ( x  1)
X+1
U - (x  1)  U 1  U  (x)
 1  ikgB 
g

x
 (x)  G(x)  (x)
g
 (x)   (x) G  (x)
G G  1
G ( x ) : Gauge transformation matrix

closed loop of gluon
U p (x)  U i (x)U j (x  1i )U i (x  1 j )U j (x)
string of gluon field
U  ( x1 )... U  ( x 2
Wilson plaquette action : Slatt  
  6  a  0.1(fm)
 TrU 
p
requires calibratio n!

 1 ) U ( x 2 )
Purely gluonic piece of continum QCD action :

d4x

x2
_

1
4g 2
6
x1
x
Tr (BB )
g2
13
Lattice gauge theory for gluons
Feynman path integral : 0 O 0
S


dU
Oe


S


dU
e

 U  O e S

After discretiza tion
: 0O0 
U  : a set of U matrices

U  e


 S
one for each link in lattice
O : the value of O operator in that configurat ion
Importance sampling : choose configurat ions with large contributi ons to the integral
14
Fermion doubling problem of
quarks on the lattice
Continuum action for a single flavor of free fermions :

_
S f  d x  (      m )
4
Fourier tr ansformation of L f :
1
Continuum inverse propagator: G -cont
( p )  i  p   m
0
Naive lattice dicretizat ion :


4
_




x 1
x 1
naive
4
Slatt,

a



m


 x

x x
f
2
a
n
  1



Fourier tr ansformation of L f :


1

lattice inverse propagator: G -latt,
naive ( p)  i
sin p  a
a
m
p


a
0

a
2 4 fermions instead of 1 !!
15
Solutions of Fermion doubling
problem
Wilson quarks
Sfw
 Sfnaive
r
 a5
2
4
  (
 x 1  2 x   x 1
x
x
 1`
a
2
)
r  Wilson parameter
Problem : Larger discretiza tion errors!
a  0  Sfw  Sfnaive
Staggered quarks
Interpretation of doublers as diffrent flavours
Problem : Flavour changing scattering (from p  0 to p  /a)!
16
Action with quarks
S
 dUd[d ] e
 (Sg   M )

 dU (det M) e
Sg
M : matrix of dynamical quark masses and depends on the quark formulatio n
det M causes big numerical problems!!
Quenched approximat ion
Forget about thedynamics of sea quarks
chiral extrapolat ion
Work with heavier quarks and extrapolat ion of light quarks like u and d
17
Relating lattice results to physics
Make the correlators of quarks by using  matrices

r

0
(  ) 0
T

(  ) T
mesons with spin
( 5  ) 0

( 5  ) T pseudoscalar
( i  ) 0

( i  ) T vector
relative spatial distribution (r) :
.
.  (x) (r)    ( x  r )  Pr obability Density of quarks  Hadron masses
18
Steps of typical lattice calculation
1- choose the lattice spacing
- close to the continuum
- computation costs
2- Choose a quark formulation and number of quark flavors
3- generating an ensemble of gluon configurations
- Try to go near small masses
- computation costs
4- calculation of quark propagators on each gluon configuration
5- combination of quark propagators to form hadron correlators
6- Determination of lattice spacing in Gev(lattice calibration)
7- extrapolation of hadron masses as a function of bare quark masses
8- repeat the calculation using several lattice spacing to compare with physical
results at the limit of a
0
9- compare with experiment or give a prediction for experiment
19
Some results of lattice QCD
calculations
The spectrum of light mesons and baryons in the quenched approximation
20
The ratio of inverse lattice spacing
21
The massesof  and K* mesonsas a functionof lattice spacing
22
c 

JPC
Charmonium spectrum in quenched approximation
23
Summary
- Photons don’t carry any colour charge, so QED is analytically solvable.
- Gluons do carry colour charge,so to solve the QCD theory, approximations are proposed
(e.g. Lattice calculation method ).
- There is a fermion doubling problem in lattice which can be solved by various methods.
- In order to obtain light quark properties, we need bigger computers and the
calculation costs will be increased.
- Quenched approximation is reasonable in order to decrease the computation costs.
24