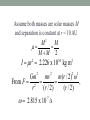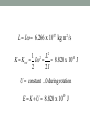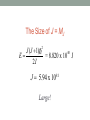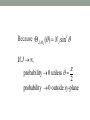* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download A Binary Star as a Quantum System
Renormalization wikipedia , lookup
Identical particles wikipedia , lookup
Scalar field theory wikipedia , lookup
Renormalization group wikipedia , lookup
Quantum dot wikipedia , lookup
Atomic orbital wikipedia , lookup
Quantum field theory wikipedia , lookup
Measurement in quantum mechanics wikipedia , lookup
Density matrix wikipedia , lookup
Rigid rotor wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
Quantum fiction wikipedia , lookup
Double-slit experiment wikipedia , lookup
Bell's theorem wikipedia , lookup
Wave–particle duality wikipedia , lookup
Quantum entanglement wikipedia , lookup
Many-worlds interpretation wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Matter wave wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Path integral formulation wikipedia , lookup
Quantum computing wikipedia , lookup
Coherent states wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Quantum group wikipedia , lookup
Quantum machine learning wikipedia , lookup
History of quantum field theory wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Quantum teleportation wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Quantum key distribution wikipedia , lookup
EPR paradox wikipedia , lookup
Probability amplitude wikipedia , lookup
Particle in a box wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Quantum state wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Hidden variable theory wikipedia , lookup
Applying the Correspondence Principle to the Three-Dimensional Rigid Rotor David Keeports Mills College [email protected] Quantum Mechanical Correspondence Principle No system strictly obeys classical mechanics Instead, all systems are quantum systems, but … “Quantum systems appear to be classical when their quantum numbers are very large.” The Instructional Challenge in Presenting the Correspondence Principle Consider “obviously classical” systems and show that they are really quantum systems Correspondence Principle Applied to Fundamental Quantum Systems Particle in 1-Dimensional Box Particle in 3-Dimensional Box Harmonic Oscillator 2-Dimensional Rigid Rotor 3-Dimensional Rigid Rotor Hydrogen Atom Particle in 1-Dimensional Box æ2ö æ np x ö y (x) = ç ÷ sin ç ÷ èLø è L ø 1/2 if n ® ¥ uniform probability distribution from x = 0 to x = L Particle in 3-Dimensional Box 1 2 æ 8 ö æ nx p x ö æ nyp y ö æ nz p z ö y (x, y, z) = ç ÷ sin ç ÷ sin ç ÷ ÷ sin ç è abc ø è a ø è b ø è c ø if nx , ny , nz ® ¥ uniform probability distribution within 3-dimensional box Harmonic Oscillator yv (x) = Nv H v (a x)e -(a x)2 /2 as v ®¥ probability is enhanced at turning points 2-Dimensional Rigid Rotor y (f ) = 1 p sin ( mf ) y (f ) = 1 p cos ( mf ) if m ® ¥ all angles become equally probable In each case as a quantum number increases by 1, DE / E @ 0 System energy appears to be a continuous function, i.e., quantization not evident A Classical Three-Dimensional Rigid Rotor Consider a rigid rotor of binary star dimensions rotating in xy-plane Assume both masses are solar masses M and separation is constant at r = 10 AU 2 M M m= = M +M 2 I = mr = 2.226 x 10 kg m 2 54 2 Gm mv m(r / 2) w From F = 2 = = , r (r / 2) (r / 2) 2 2 w = 2.815 x 10 /s -7 2 2 L = Iw = 6.266 x 10 kg m /s 47 2 1 2 L K = K rot = Iw = = 8.820 x 10 40 J 2 2I 2 U = constant º 0 during rotation E = K +U = 8.820 x 10 J 40 But does this 3-D rotor really obey classical mechanics? No, it is a quantum system that only appears to obey classical mechanics because its quantum numbers are very large! Why Are Quantum Numbers Large? Eigen-Operators for 3-D Rigid Rotors 2 ù é 1 ¶ æ ö ¶ 1 ¶ Ĥ = - ê çsinq ÷ + 2 2ú 2I ë sinq ¶q è ¶q ø sin q ¶f û 2 ù é æ ö 1 ¶ ¶ 1 ¶ L̂2 = - 2 ê ç sinq ÷ + 2 2ú ¶q ø sin q ¶f û ë sinq ¶q è 2 ¶ L̂z = -i ¶f Spherical Harmonics Are Eigenfunctions Eigenvalues of Operators J(J +1) ĤYJ,M J (q, f ) = 2I 2 YJ,M J (q, f ) L̂2YJ,M J (q, f ) = J(J +1) 2YJ,M J (q, f ) L̂zYJ,M J (q, f ) = M J YJ,M J (q, f ) J = 0, 1, 2, ... M J = - J, - J +1, ... , + J For assumed orbit in the xy-plane, angular momentum and its z-component are virtually indistinguishable, so … L @ Lz J = MJ ® ¥ The Size of J = MJ J(J +1) E= 2I 2 40 = 8.820 x 10 J J = 5.94 x 10 Large! 81 Energy and the Correspondence Principle Suppose that J increases by 1: DE E(J +1) - E(J) 2 -82 = = = 3.37 x 10 E E(J) J Energy quantization unnoticed Rotor Orientation From Spherical Harmonic Wavefunctions YJ,M J (q, f ) = QJ,M J (q )FM J (f ) QJ,M J (q ) = N J,M J PJ,M J (q ) 1 F0 (f ) = 2p 1 F M J ,c (f ) = cos(M J f ) p 1 F M J ,s (f ) = sin(M J f ) p QJ,M J (q ) can be complex (-1) 2J +1 (J - M J )! M J d (sin 2 J q ) QJ,M J (q ) = J sin q J+ M J 2 J! 2 (J + M J )! [d(cosq )] J+ M J J But when J = M J , QJ,M J (q ) is very simple: QJ,M J (q ) = N J sin J q Because QJ,M J (q ) = N J sin q J If J ® ¥, probability ® 0 unless q = p 2 probability ® 0 outside xy-plane F M J ,c (f ) = 1 p cos(M J f ) 2M J angular nodes and 2M J angular antinodes If M J ® ¥, probability is proportional to Df No f is favored Localization of axis at a particular f requires superposition of wavefunctions with a range of angular momentum values Uncertainty principle: Angular certainty comes at the expense of angular momentum certainty The Hydrogen Atom Problem in the Large Quantum Number Limit: Consider Earth-Sun System GmS m Ñ yy = Ey 2m r 2 2 - 2 Ñ y2 2me e 2 y 4pe0 r = Ey Results for Quantum Earth n =1, 2,3,... l = 0,1, 2,..., n -1 ml = 0,±1,±2,...,±l Gmm 1 E =2 2 2 n L = l(l +1) 2 3 Lz = ml 2 S Assumed circular orbit implies n @ l = ml ® ¥ consistent with correspondence principle ynlm (r, q, f ) = Rnl (r)Qlm (q )Fm (f ) With n @ l = ml ® ¥, ynlm (r, q, f ) implies that Earth’s l l l l spatial probability distribution is y 0 Earth is in a hydrogen-like orbital characterized by huge quantum numbers x Quantum Mechanical Earth: Where Orbitals Become Orbits. European Journal of Physics, Vol. 33, pp. 1587-98 (2012) End