Download عرض+تقديم..

In algebra, we work with the set of real numbers, which we can model using a number
line.
Real numbers describe real-world quantities such as amounts, distances, age,
temperature, and so on. A real number can be an integer, a fraction, or a decimal. They
can also be either rational or irrational. Numbers that are not "real" are called
imaginary. Imaginary numbers are used by mathematicians to describe numbers that
cannot be found on the number line. They are a more complex subject than we will
work with here
In this lesson we look at some
properties that apply to all real
numbers. If you learn these
properties, they will help you solve
problems in algebra. Let's look at each
property in detail, and apply it to an
algebraic expression.
The commutative property of addition says
that we can add numbers in any order. The
commutative property of multiplication is very
similar. It says that we can multiply numbers in
any order we want without changing the
result.
addition
5a + 4 = 4 + 5a
multiplication
3 x 8 x 5b = 5b x 3 x 8
Both addition and multiplication can actually be done
with two numbers at a time. So if there are more
numbers in the expression, how do we decide which
two to "associate" first? The associative property of
addition tells us that we can group numbers in a sum
in any way we want and still get the same answer. The
associative property of multiplication tells us that we
can group numbers in a product in any way we want
and still get the same answer.
addition
(4x + 2x) + 7x = 4x + (2x + 7x)
multiplication
2x2(3y) = 3y(2x2)
The distributive property comes into play when an expression
involves both addition and multiplication. A longer name for it is,
"the distributive property of multiplication over addition." It tells
us that if a term is multiplied by terms in parenthesis, we need to
"distribute" the multiplication over all the terms inside.
2x(5 + y) = 10x + 2xy
Even though order of operations says that you must add
the terms inside the parenthesis first, the distributive
property allows you to simplify the expression by
multiplying every term inside the parenthesis by the
multiplier. This simplifies the expression.
The density property tells us that we can always find
another real number that lies between any two real
numbers. For example, between 5.61 and 5.62, there is
5.611, 5.612, 5.613 and so forth.
Between 5.612 and 5.613, there is 5.6121, 5.6122 ...
and an endless list of other numbers!
The identity property for addition tells us that zero
added to any number is the number itself. Zero is
called the "additive identity." The identity property for
multiplication tells us that the number 1 multiplied
times any number gives the number itself. The number
1 is called the "multiplicative identity."
Addition
5y + 0 = 5y
Multiplication
2c × 1 = 2c
Adding Real Numbers
This tutorial reviews adding real numbers
as well as finding the additive inverse or
opposite of a number
Adding Real Numbers
with the same sign
Step 1: Add the absolute values
Step 2: Attach their common sign to sum
.
In other words:
If both numbers that you are adding are positive, then you
will have a positive answer.
If both numbers that you are adding are negative then you
will have a negative answer.
Example 1:
Add -6 + (-8).
-6 + (-8) = -14
.
The sum of the absolute values would be 14 and their
common sign is -. That is how we get the answer of -14.
You can also think of this as money. I know we can all
relate to that. Think of the negative as a loss. In this
example, you can think of it as having
lost 6 dollars and then having lost
another 8 dollars for a total loss of 14
dollars.
Example 2:
Add -5.5 + (-8.7).
-5.5 + (-8.7) = -14.2
.
The sum of the absolute values would be 14.2 and their
common sign is -. That is how we get the answer of -14.2.
You can also think of this as money - I know we can all
relate to that. Think of the negative as a loss. In this
example, you can think of it as having
lost 5.5 dollars and then having lost
another 8.7 dollars for a total loss of
14.2 dollars.
The Real Numbers
Sets of Numbers
* Natural Numbers {1, 2, 3, 4, . . .}
* Whole Numbers {0, 1, 2, 3, 4, . . .}
* Integers {. . . , -3, -2, -1, 0, 1, 2, 3, . . .}
Rational Numbers { | p and q are integers and q ¹ 0 }
The set of rational numbers contains all numbers that can be written
as fractions, or quotients of integers. Integers are also rational
numbers since they can be represented as fractions. All decimals that
repeat or terminate belong to the set of rational numbers. The
following are all rational numbers:
= . . . 0.6666 ,
= 0.125 ,
=0,
= 5- ,
1,
-,
-,
Irrational Numbers
{x | x is real but not rational }
The irrational numbers are nonrepeating,
nonterminating decimals. They cannot be represented
as the quotient of two integers. The following are all
irrational numbers :
p, ,-
Real Numbers {x | x corresponds to a point on
the number line }
The set of real numbers consists of all the rational numbers
together with all the irrational numbers.
Example
Given set A = { ,- , 0, 2.9, -5, 4, - , , -7 , p}, list all the
elements of A that belong to the set of :
a) natural numbers,
b) whole numbers,
c) integers,
d) rational numbers,
e) irrational numbers,
f) real numbers.
Order of Operations
1. Perform operations in grouping symbols (parentheses, brackets,
braces, or fraction bars). Start with the innermost and work outward.
2. Calculate powers and roots, working from left to right.
3. Perform multiplication and division in order from left to right.
4. Perform addition and subtraction in order from left to right.
Example
Use order of operations to evaluate:
a) 6(-5) – (-3)(2)
b)
c) -9 – {6 – 2[12 – (8 – 15)] – 4}
Solution:
a) 6(-5) – (-3)(2) = 6(-5) – (-3)(16) No grouping symbols; power
calculated first
= -30 – (-48) Multiplication performed
= -30 + 48 Subtraction changed to addition
= 18 Addition performed
Solution:
b) Begin by simplifying the numerator and denominator of fraction.
=
=
=
=
Calculate powers firs
Perform multiplications
Perform additions and subtractions
Simplify
c) -9 – {6 – 2[12 – (8 – 15)] – 4} = -9 – {6 – 2[12 – (-7)] – 4}
Start with innermost grouping symbol, parentheses, and
subtract
= -9 – {6 – 2[19] – 4} Working outward, perform
subtraction in brackets
= -9 – {6 – 38 – 4} Within braces, multiply
= -9 – {-36} Within braces, subtract
= -9 + 36 Change subtraction to addition
= 27 Add
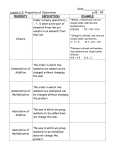
Properties of the Real Numbers
For all real numbers a, b, and c:
1. Commutative Property for Addition: a + b = b + a
2. Commutative Property for Multiplication: ab = ba
The commutative properties state that two numbers may be added or
multiplied in any order.
Properties of the Real Numbers
For all real numbers a, b, and c:
3. Associative Property for Addition: a + (b + c) = (a + b) + c
4. Association Property for Multiplication: a(bc) = (ab)c
For the associative properties, the order of the terms or factors
remains the same; only the grouping is changed.
Properties of the Real Numbers
For all real numbers a, b, and c:
5. Identity Property for Addition: There is a unique real number, 0,
such that a + 0 = a and 0 + a = a
The identity property for addition tells us that adding 0 to any number
will not change the number.
6. Identity Property for Multiplication: There is a unique real number,
1, such that a·1 = a and 1·a = a
The identity property for multiplication tells us that multiplying any
number by 1 will not change the number.
Properties of the Real Numbers
For all real numbers a, b, and c:
7. Inverse Property for Addition: Each nonzero real number a has a
unique additive inverse, represented by –a, such that
a + (-a) = 0 and –a + a = 0
Additive inverses are called opposites.
8. Inverse Property for Multiplication: Each nonzero real number a
has
unique multiplicative inverse, represented by , such that
and
Multiplicative inverses are called
reciprocals.
Properties of the Real Numbers
For all real numbers a, b, and c:
9. Distributive Property: a(b + c) = ab + ac
Example:
Identify the property illustrated in each statement:
a) (x + 7) + 8 = x + (7 + 8)
b) 4x + 0 = 4x
c) 10 · ( x) = (10 · )x
d) (x + 1) ·
=1
e) 4(x + 5) = 4x + 20
f) 3 · (5 · a) = 3 · (a · 5)
g) -6x + 6x = 0
h) (2 + y) + 5 = 5 + (2 + y)
i) (y + 5)(y – 3) = (y – 3)(y + 5)
j) 5 · 1 = 5
Solution:
a) Associative Property for Addition. Order of terms
remains the same. Only the grouping changes.
b) Identity Property for Addition. Adding zero to
something does not change it.
c) Associative Property for Multiplication. Order of factors
is the same. Only the grouping changes
Solution:
d) Inverse Property for Multiplication. The product of
reciprocals is 1.
e) Distributive Property.
f) Commutative Property for Multiplication. Order of the
factors is changed.
Solution:
g) Inverse Property for Addition. The sum of opposites is 0.
h) Commutative Property for Addition. The order of the
terms is changed.
i) Commutative Property for Multiplication. The order of
the factors is changed.
j) Identity Property for Multiplication. Multiplying
a number by 1 does not change it.
The Set of Real Numbers
First, a few terms:
Terminating Decimal: A decimal that ends, having a
finite number of digits after the decimal point.
Sample: 3/4 = 0.75
The Set of Real Numbers
First, a few terms:
Repeating Decimal: A decimal that doesn't end; it
shows a repeating pattern of digits after the
decimal point. Sample: 1/3 = 0.3333...
Exponents
Exponents are used in many algebra problems, so
it's important that you understand the rules for
working with exponents. Let's go over each rule in
detail, and see some examples.
Exponents
Rules of 1
There are two simple "rules of 1" to remember.
First, any number raised to the power of "one" equals itself. This
makes sense, because the power shows how many times the
base is multiplied by itself. If it's only multiplied one time, then
it's logical that it equals itself.
Secondly, one raised to any power is one. This, too, is logical,
because one times one times one, as many times as you multiply
it, is always equal to one.
Exponents
Product Rule
The exponent "product rule" tells us that, when multiplying two
powers that have the same base, you can add the exponents. In
this example, you can see how it works. Adding the exponents is
just a short cut!
Exponents
Product Rule
The exponent "product rule" tells us that, when multiplying two
powers that have the same base, you can add the exponents. In
this example, you can see how it works. Adding the exponents is
just a short cut!
Exponents
Quotient Rule
The quotient rule tells us that we can divide two powers with the
same base by subtracting the exponents. You can see why this
works if you study the example shown.
Exponents
Zero Rule
According to the "zero rule," any nonzero number raised to the
power of zero equals 1.
Exponents
Negative Exponents
The last rule in this lesson tells us that any nonzero number
raised to a negative power equals its reciprocal raised to the
opposite positive power.