Download complex number - Deeteekay Community

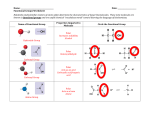
ET 201 ~ ELECTRICAL
CIRCUITS
COMPLEX NUMBER SYSTEM
 Define and explain complex number
Rectangular form
Polar form
Mathematical operations
(CHAPTER 2)
1
COMPLEX
NUMBERS
2
2. Complex Numbers
• A complex number
represents a point in
a two-dimensional
plane located with
reference to two
distinct axes.
• This point can also
determine a radius
vector drawn from the
origin to the point.
• The horizontal axis is
called the real axis,
while the vertical axis
is called the
imaginary ( j ) axis. 3
2.1 Rectangular Form
• The format for the
rectangular form is
• The letter C was
chosen from the
word complex
• The bold face (C)
notation is for any
number with
magnitude and
direction.
• The italic notation is
for magnitude only.
4
2.1 Rectangular Form
Example 14.13(a)
Sketch the complex number C = 3 + j4 in the
complex plane
Solution
5
2.1 Rectangular Form
Example 14.13(b)
Sketch the complex number C = 0 – j6 in the
complex plane
Solution
6
2.1 Rectangular Form
Example 14.13(c)
Sketch the complex number C = -10 – j20 in
the complex plane
Solution
7
2.2 Polar Form
• The format for the
polar form is
• Where:
Z : magnitude only
q : angle measured
counterclockwise
(CCW) from the
positive real axis.
• Angles measured in
the clockwise direction
from the positive real
axis must have a
negative sign
associated with them. 8
2.2 Polar Form
 C   Zq  Zq  180

9
2.2 Polar Form
Example 14.14(a)
C  530

Counterclockwise (CCW)
10
2.2 Polar Form
Example 14.14(b)
C  7  120

Clockwise (CW)
11
2.2 Polar Form
 C   Zq  Zq  180
Example 14.14(c)
C   4.260

 4.260  180

 4.2240


12
14.9 Conversion Between Forms
1. Rectangular to Polar
13
14.9 Conversion Between Forms
2. Polar to Rectangular
14
2.3 Conversion Between Forms
Example 14.15
Convert C = 4 + j4 to polar form
Solution
Z  3 4 5
3
2
4

q  tan    53.13
3
1
C  553.13

15
2.3 Conversion Between Forms
Example 14.16
Convert C = 1045 to rectangular form
Solution
X  10 cos 45  7.07

Y  10 sin 45  7.07

C  7.07  j 7.07
16
2.3 Conversion Between Forms
Example 14.17
Convert C = - 6 + j3 to polar form
Solution
Z  6  3  6.71
2
2
3
q  180  tan  
6
1

 153.43

C  6.71153.43

17
2.3 Conversion Between Forms
Example 14.18
Convert C = 10  230 to rectangular form
Solution
X  10 cos 230   6.43
Y  10 sin 230   7.66

C  6.43  j 7.66
18
2.4 Mathematical Operations with
Complex Numbers
• Complex numbers lend themselves readily to
the basic mathematical operations of addition,
subtraction, multiplication, and division.
• A few basic rules and definitions must be
understood before considering these
operations:
19
2.4 Mathematical Operations with
Complex Numbers
Complex Conjugate
• The conjugate or complex conjugate of
a complex number can be found by simply
changing the sign of the imaginary part in
the rectangular form or by using the
negative of the angle of the polar form
20
2.4 Mathematical Operations with
Complex Numbers
Complex Conjugate
In rectangular form, the
conjugate of:
C = 2 + j3
is
2 – j3
21
2.4 Mathematical Operations with
Complex Numbers
Complex Conjugate
In polar form, the
conjugate of:
C = 2  30o
is 2 30o
22
2.4 Mathematical Operations with
Complex Numbers
Reciprocal
• The reciprocal of a complex number is 1
divided by the complex number.
• In rectangular form, the reciprocal of:
C  X  jY
is
1
X  jY
• In polar form, the reciprocal of:
C  Zq
is
1
Z q
23
2.4 Mathematical Operations with
Complex Numbers
Addition
• To add two or more complex numbers, simply
add the real and imaginary parts separately.
24
2.4 Mathematical Operations with
Complex Numbers
Example 14.19(a)
C1  2  j 4;
C2  3  j1
Find C1 + C2.
Solution
C1  C2  2  3  j4  1
 5  j5
25
2.4 Mathematical Operations with
Complex Numbers
Example 14.19(b)
C1  3  j6;
C2  6  j3
Find C1 + C2
Solution
C1  C2  3  6  j6  3
 3  j 9
26
2.4 Mathematical Operations with
Complex Numbers
Subtraction
• In subtraction, the real and imaginary parts are
again considered separately .
NOTE
Addition or subtraction cannot be performed in polar form
unless the complex numbers have the same angle ө or
unless they differ only by multiples of 180°
27
2.4 Mathematical Operations with
Complex Numbers
Example 14.20(a)
C1  4  j 6;
C2  1  j 4
Find C1 - C2
Solution
C1  C2  4 1  j6  4
 3  j2
28
2.4 Mathematical Operations with
Complex Numbers
Example 14.20(b)
C1  3  j3;
C2  2  j5
Find C1 - C2
Solution
C1  C2  3  2  j3  5
 5  j2
29
2.4 Mathematical Operations with
Complex Numbers
Example 14.21(a)
245  345  545
NOTE
Addition or subtraction cannot be performed in polar form
unless the complex numbers have the same angle ө or
unless they differ only by multiples of 180°
30
2.4 Mathematical Operations with
Complex Numbers
Example 14.21(b)
20  4180  60
NOTE
Addition or subtraction cannot be performed in polar form
unless the complex numbers have the same angle ө or
unless they differ only by multiples of 180°
31
2.4 Mathematical Operations with
Complex Numbers
Multiplication
• To multiply two complex numbers in rectangular
form, multiply the real and imaginary parts of one
in turn by the real and imaginary parts of the
other.
• In rectangular form:
• In polar form:
32
2.4 Mathematical Operations with
Complex Numbers
Example 14.22(a)
C1  2  j3;
C2  5  j10
Find C1C2.
Solution
C1 C2  2  j35  j10
 20  j 35
33
2.4 Mathematical Operations with
Complex Numbers
Example 14.22(b)
C1  2  j3; C2  4  j6
Find C1C2.
Solution
C1 C2   2  j34  j6
 26  26180
34
2.4 Mathematical Operations with
Complex Numbers
Example 14.23(a)
C1  520 ;
C2  1030
Find C1C2.
Solution

C1 C2  5 10 20  30

 5050
35
14.10
Mathematical Operations with
Complex Numbers
Example 14.23(b)
C1  2  40 ;
C2  7120
Find C1C2.
Solution

C1  C2  2  7  40  120

 1480
36
14.10
Mathematical Operations with
Complex Numbers
Division
• To divide two complex numbers in rectangular
form, multiply the numerator and denominator
by the conjugate of the denominator and the
resulting real and imaginary parts collected.
• In rectangular form:
• In polar form:
37
2.4 Mathematical Operations with
Complex Numbers
Example 14.24(a)
C1  1  j 4;
C2  4  j5
Find
C1
C2
Solution
C1 1  j 4 4  j 5 1  j 4 4  j 5



C 2 4  j 5 4  j 5 4  j 54  j 5
24  j11

 0.59  j 0.27
16  25
38
2.4 Mathematical Operations with
Complex Numbers
Example 14.24(b)
C1  4  j8; C2  6  j1
Find
C1
C2
Solution
C1  4  j8 6  j1  4  j86  j1



C2
6  j1 6  j1 6  j16  j1
 16  j 52

 0.43  j1.41
36  1
39
2.4 Mathematical Operations with
Complex Numbers
Example 14.25(a)
C1  1510 ; C2  27


Find
C1
C2
Solution
C1 1510 15







10

7

C2
27
2
 7.33
40
2.4 Mathematical Operations with
Complex Numbers
Example 14.25(b)
C1  8120 ; C2  16  50


Find
C1
C2
Solution
C1
8120
8







120


50

C2 16  50 16
 0.5170
41
2.4 Mathematical Operations with
Complex Numbers
• Addition
• Subtraction
• Multiplication
• Division
• Reciprocal
• Complex conjugate
• Euler’s identity
z1  z2  ( x1  x2 )  j( y1  y2 )
z1  z2  ( x1  x2 )  j( y1  y2 )
z1 z2  r1r2 1  2
z1
r1

1   2
z2
r2
1
1

 
z
r
z   x  jy  r     re  j
e  j  cos   j sin 
42