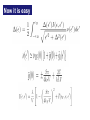Download Seoul National University, Korea, 06/2010, Insuk Yu

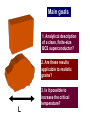
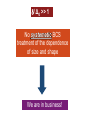
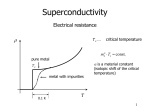
An excursion into modern
superconductivity: from
nanoscience to cold atoms and holography
Antonio M. García-García
Yuzbashyan
Rutgers
Richter
Regensburg
Altshuler
Columbia
Sangita Bose, Tata,
Max Planck Stuttgart
Urbina
Regensburg
Kern
Stuttgart
Diego Rodriguez Masaki Tezuka
Queen Mary
Kyoto
Sebastian Franco
Santa Barbara
Jiao Wang
NUS
Superconductivity in
nanograins
Practical
New forms of
superconductivity
Superconductivity
Increasing the
superconductor
Tc
Technical
New tools
String Theory
Theoretical
Enhancement and control of
superconductivity in nanograins
Phys. Rev. Lett. 100,
187001 (2008)
Yuzbashyan
Rutgers
Altshuler
Columbia
Sangita Bose, Tata,
Max Planck Stuttgart
arXiv:0911.1559
Nature Materials
Richter
Regensburg
Urbina
Regensburg
Kern
Ugeda, Brihuega
Main goals
1. Analytical description
of a clean, finite-size
BCS superconductor?
2. Are these results
applicable to realistic
grains?
3. Is it possible to
increase the critical
temperature?
L
The problem
BCS gap equation
V bulk
Δ~ De-1/
Can I combine
this?
Semiclassical 1/kF L <<1
Berry, Gutzwiller, Balian
V finite
Δ=?
?
Is it already
done?
Relevant Scales
Δ0 Superconducting gap
L typical length
 Mean level spacing
l coherence length
F Fermi Energy
ξ Superconducting
coherence length
Conditions
BCS
/ Δ0 << 1
Semiclassical
1/kFL << 1
Quantum coherence
l >> L ξ >> L
For Al the optimal region is L ~ 10nm
Maybe it is possible
Go ahead!
Corrections
to BCS
smaller or
larger?
Let’s think about this
This has not been
done before
It is possible but,
is it relevant?
If so, in what range of
parameters?
A little history
Superconductivity in
particular geometries
Parmenter, Blatt, Thompson (60’s) : BCS in a rectangular grain
Heiselberg (2002): BCS in harmonic potentials, cold atom appl.
Shanenko, Croitoru (2006): BCS in a wire
Devreese (2006): Richardson equations in a box
Kresin, Boyaci, Ovchinnikov (2007) Spherical grain, high Tc
Olofsson (2008): Estimation of fluctuations in BCS, no correlations
Nature of superconductivity (?)
in ultrasmall systems
Breaking of superconductivity for
/ Δ0 > 1?
Estimation. No rigorous!
Anderson (1959)
Thermodynamic properties
Muhlschlegel, Scalapino (1972)
Experiments
Tinkham et al. (1995) . Guo et al., Science
306, 1915, Superconductivity Modulated by
quantum Size Effects.
T = 0 and / Δ0 > 1
(1995-)
Richardson, von Delft, Braun, Larkin,
Sierra, Dukelsky, Yuzbashyan
Description beyond BCS
Even for / Δ0 ~ 1 there is
“supercondutivity
1.Richardson’s equations:
Good but Coulomb, phonon
spectrum?
2.BCS fine until / Δ0 ~ 2
/ Δ0 >> 1
No systematic BCS
treatment of the dependence
of size and shape
We are in business!
Hitting a bump
λ/V ?
In,n should admit a
semiclassical expansion
but how to proceed?
I ~1/V?
Fine, but the
matrix
elements?
For the cube
yes but for a
chaotic grain
I am not sure
From desperation to hope
?
A
B
VI ( ,  ' ) 
 2 2  f (   ' ,  F , L)
kF L kF L
Yes, with help,
we can
Regensburg, we have got a problem!!!
Do not worry. It is not
an easy job but you are
in good hands
Nice closed
results that do
not depend on
the chaotic
cavity
For l>>L ergodic
theorems assures
universality
f(L,- ’, F) is a
simple function
A few
months
later
Semiclassical (1/kFL >> 1) expression
of the matrix elements valid for l >> L!!
ω = -’
Relevant in any mean field approach with
chaotic one body dynamics
Now it is easy
3d chaotic
Sum is cut-off ξ
Boundary
conditions
Universal function
Enhancement of SC!
3d chaotic
Al grain
kF = 17.5 nm-1
 = 7279/N mV
0 = 0.24mV
L = 6nm, Dirichlet, /Δ0=0.67
For L< 9nm leading
correction comes
from I(,’)
L= 6nm, Neumann, /Δ0,=0.67
L = 8nm, Dirichlet, /Δ0=0.32
L = 10nm, Dirichlet, /Δ0,= 0.08
3d integrable
Numerical & analytical
Cube & rectangle
From theory to
experiments
Real (small) Grains
L ~ 10 nm Sn, Al…
Is it taken into
account?
Coulomb interactions
No, but screening
should be effective
Surface Phonons
No, but no strong
effect expected
Deviations from mean field
Yes
Decoherence
Yes
Fluctuations
No
Mesoscopic corrections versus
corrections to mean field
Finite size
corrections to BCS
Matveev-Larkin
Pair breaking
Janko,1994
The leading mesoscopic corrections
contained in (0) are larger
The correction to (0) proportional to 
has different sign
Experimentalists are coming
Sorry but in
Pb only
small
fluctuations
Are you
300% sure?
arXiv:0904.0354v1
However
in Sn is
very
different
!!!!!!!!!!!!!
!!!!!!!!!!!!!
!!!
Pb and Sn are very different because their
coherence lengths are very different.
5.33 Å
7 nm
I
V
STM tip
Å 33.5
Pb/Sn
nano-particle
BN
Rh(111)
0.0
0Å 0nm
dI/dV
 (T )
Theory
+
Direct observation of thermal fluctuations
and the gradual breaking of
superconductivity in single, isolated Pb
nanoparticles
Pb
?
Theoretical
description of
dI/dV
?
 (T )
dI/dV
Dynes
formula
Solution
Thermal fluctuations + BCS Finite size
effects + Deviations from mean field
Dynes fitting
Problem:  > 
How?
Finite T
Thermal fluctuations
Static Path approach
BCS finite size effects
Part I
Deviations from BCS
Richardson formalism
No quantum fluctuations!
T=0
BCS finite size effects
Part I
Deviations from BCS
Richardson formalism
Altshuler, Yuzbashyan, 2004
No quantum fluctuations!
Not important h ~ 6nm
Cold atom physics and novel
forms of superconductivity
Cold atoms
settings
Temperatures can be lowered
up to the nano Kelvin scale
Interactions can be controlled
by Feshbach resonances
Ideal
laboratory to
test quantum
phenomena
Until
2005
2005 - now
1. Disorder &
magnetic fields
Test of Anderson
localization, Hall Effect
2. Non-equilibrium
effects
Test ergodicity hypothesis
3. Efimov physics
Bound states of three
quantum particles do exist
even if interactions are
repulsive
What is the effect of disorder
in 1d Fermi gases?
Stability of the superfluid state in a disordered 1D ultracold fermionic gas
Masaki Tezuka (U. Tokyo), Antonio M. Garcia-Garcia
arXiv:0912.2263
DMRG analysis of
Why?
Only two types of disorder can be
implemented experimentally
Speckel potential
speckle
Modugno
Our model!!
incommensurate lattice
pure random with correlations
quasiperiodic
localization for any 
localization transition at finite   2
Results I
Attractive interactions
enhance localization
U=1
c = 1<2
Results II
Weak disorder enhances
superfluidity
Results III
A pseudo gap
phase exists.
Metallic
fluctuations
break long
range order
Results IV
Spectroscopic
observables are
not related to long
range order
String theory meets
condensed matter
Strongly coupled
field theory
N=4 Super-Yang Mills
CFT
Why?
Weakly coupled
gravity dual
Anti de Sitter space
AdS
Applications in high Tc
superconductivity
Powerful tool to deal with
strong interactions
Why
now?
New field.
Potential for high impact
JHEP 1004:092 (2010)
What is
next?
Transition from qualitative
to quantitative
Phys. Rev. D 81, 041901 (2010)
Collaboration with string theorists
Problems
1. Estimation of the validity of the AdS-CFT approach
2. Large N limit
For what condensed matter systems
these problems are minimized?
Phase Transitions triggered by thermal
fluctuations
Why?
1. Microscopic Hamiltonian is not important
2. Large N approximation OK
Holographic approach to phase transitions
Phys. Rev. D 81, 041901 (2010)
1. d=2 and AdS4 geometry
2. For c3 = c4 = 0 mean field results
3. Gauge field A is U(1) and  is a scalar
4. A realization in string theory and M theory is
known for certain choices of ƒ
5. By tuning ƒ we can reproduce many
types of phase transitions
Results I
For c4 > 1 or c3 > 0 the transition becomes first order
A jump in the condensate at the
critical temperature is clearly
observed for c4 > 1
The discontinuity for c4 > 1 is
a signature of a first order
phase transition.
Results II
1. For c3 < -1
2. For
Second order phase transitions with non mean field
critical exponents different are also accessible
O2  T  Tc

  1  1/ 2
  2  1    1/ 2
Condensate for c = -1
and c4 = ½. β = 1, 0.80,
0.65, 0.5 for  = 3, 3.25,
3.5, 4, respectively
1

 2
Results III
The spectroscopic gap becomes larger and
the coherence peak narrower as c4
increases.
Future
1. Extend results to β <1/2
2. Adapt holographic techniques to spin discrete
3. Effect of phase fluctuations. Mermin-Wegner
theorem?
4. Relevance in high temperature superconductors
THANKS!
Unitarity regime
and Efimov states
3 identical bosons with a large scattering length a
Energy
Efimov trimers
Bound states exist even
for repulsive interactions!
3 particles
1/a
trimer
Predicted by V.
Efimov in 1970
trimer
Ratio
= 514
Bond is purely
quantum- mechanical
trimer
Naidon,
Tokyo
Form an infinite series
(scale invariance)
What would I bring to Seoul
National University?
Expertise in interesting problems in condensed
matter theory
Cross disciplinary profile and interests with the
common thread of superconductivity
Teaching and leadership experience from a top US
university
Collaborators
Decoherence and
geometrical deformations
Decoherence effects and small geometrical
deformations weaken mesoscopic effects
How much?
To what extent is
our formalism
applicable?
Both effects can be
accounted analytically by
using an effective cutoff in
the trace formula for the
spectral density
Our approach provides an effective
description of decoherence
Non oscillating
deviations present
even for L ~ l
What
next?
Quantum Fermi gases
From few-body to many-body
Discovery of new forms
of quantum matter
Relation to high Tc
superconductivity
Holographic approach to phase transitions
Phys. Rev. D 81, 041901 (2010)
1. A condensate that is non zero at low T and that
vanishes at a certain T = Tc
2. It is possible to study different phase transitions
3. A string theory embedding is known
A U(1) field
, p scalars
F Maxwell tensor
E. Yuzbashyan,
Rutgers
B. Altshuler
Columbia
JD Urbina
Regensburg
S. Bose
Stuttgart
M. Tezuka
Kyoto
K. Richter
Regensburg
Let’s do
it!!
D. Rodriguez
Queen Mary
J. Wang
Singapore
P. Naidon
Tokyo
K. Kern,
Stuttgart
S. Franco,
Santa Barbara