* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Quantum Electro-Dynamical Time-Dependent Density Functional
Schrödinger equation wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Wave–particle duality wikipedia , lookup
Quantum field theory wikipedia , lookup
Renormalization wikipedia , lookup
Probability amplitude wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Quantum state wikipedia , lookup
Renormalization group wikipedia , lookup
Coherent states wikipedia , lookup
Hidden variable theory wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Hydrogen atom wikipedia , lookup
Dirac equation wikipedia , lookup
Path integral formulation wikipedia , lookup
Scalar field theory wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Lattice Boltzmann methods wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
History of quantum field theory wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Canonical quantization wikipedia , lookup
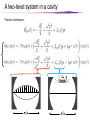
Quantum Electro-Dynamical Time-Dependent Density Functional Theory on a Lattice Lattice-QED-TDDFT Mehdi Farzanehpour, Ilya Tokatly Nano-bio spectroscopy group, University of Basque Country San Sebastian, Spain eman ta zabal zazu [email protected] Universidad del País Vasco Euskal Herriko Unibertsitatea nano-bio spectroscopy group What is Time dependent density functional theory? TDDFT is a formulation of the quantum many-body problem based on the 1:1 map from the time-dependent density potential to the driving external . A lattice example: Many electrons on an M-site lattice subject to an external classical electric field. What is Time dependent density functional theory? TDDFT is a formulation of the quantum many-body problem based on the 1:1 map from the time-dependent density potential to the driving external .[1] A lattice example: Many electrons on an M-lattice subject to external classical electric field. It can be shown that the time dependent state of the system and on-site potential are unique functionals of the on-site density provided that the density and initial state satisfy some well defined conditions.[2] [1] E. Runge and E. K. U. Gross, PRL. 52, 997 (1984) [2] M. Farzanehpour and I. V. Tokatly, PRB 86,125130 (2012). Why QED-TDDFT? ● Superconducting qubit using circuit quantum electrodynamics ● Atoms in optical cavity ● Molecules interacting with cavity photons H. Mabuchi and A. Doherty,Science 298,1372 (2002) A. Blais etal. .PRA 69, 062320 (2004) What is QED-TDDFT? QED-TDDFT is a generalization of TDDFT for electronic systems interacting with quantized electromagnetic field. [1] I. V. Tokatly, PRL. 110, 233001 [2] M. Ruggenthaler etal PRA. 90, 012508 [3] Mehdi Farzanehpour, I. V. Tokatly, PRB 90, 195149 [4] C. Pellegrini etal, Arxiv 1412.4530 An example system A two-level system coupled with a single cavity mode: Schrödinger Equation: A two-level system in a cavity Electronic Hamiltonian: Hopping On-site potential A two-level system in a cavity Photonic Hamiltonian: A two-level system in a cavity Interaction Hamiltonian: Basic variables Here we need to define a set of basic variables: 1. On-site density 2. Expectation value of the photonic coordinate: Direct map Given the Schrödinger equation and the initial state unique map from the time dependent on-site potential external current to the on-site density of the photonic coordinate SE: . , there is a and the and expectation value “Inverse” map Statement of the theorem: The electron-photon wave function unique functional of the electronic density value of the photonic coordinate and the density and the expectation , provided the initial state satisfy a set of well defined conditions. is a How we show the “inverse” map? From the equation for the second derivative of the density and the field average: (Driven harmonic oscillator) (Divergence of the force balance equation) How we show the “inverse” map? So we will have a set of equations which form a Non-linear SE NLSE: This is a set of semi-linear partial differential equations where Irving Segal showed that it has a unique solution if continuous in time. [1] I. Segal, Annals of Mathematics, 78, 339(1963) is Lipschitz and What else? 1. This formalism can easily generalized to many electron on a lattice coupled to many photonic modes. [1] 2. Not all densities on a lattice are v-representable. 3. However dynamics starting from the ground state density are guaranteed to be v-representable.[1] (v-representability: A time dependent density is v-representable if exists a time evolution with a time-dependent potential which reproduces the density.) [1] Mehdi Farzanehpour, I. V. Tokatly, PRB 90, 195149 Thank you [email protected]