Download File - Miss Pereira

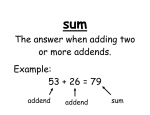
Lesson 1.1
Real Numbers and Number Operations
Algebra 2
Miss Pereira
Warm Up
 Simplify:
 1.
 2.
 3.
12 x (-12) =
-23 + (-15) =
28 ÷ (-12) =
 Order the numbers from least to greatest
 4.
 5.
.314, .0978, .309, .31
1 1 2 3
, , ,
2 3 5 16
Types of Numbers
Types of Numbers
Types of Numbers:
In words:
Whole Numbers
Numbers with no fractional parts,
decimals, or negatives.
Integers
Numbers with no fractional parts.
Includes positive and negative whole
numbers
Rational Numbers
Numbers that can be written as the ratio
of 2 integers
They terminate or repeat
Irrational Numbers
Numbers that, as decimals, don’t
terminate or repeat.
In numbers:
The Real Number Line
 Real numbers can be pictured as points on a line called
a real number line. Numbers increase from left to right,
and the point labeled 0 is the origin.
 (on the graph below, label origin, positive and negative
numbers)
The Real Number Line
 Drawing a point is called graphing or plotting the
point. The number that corresponds to a point on the
number line is the coordinate of the point.
 Number lines are used to order real numbers.
 To show the order of two numbers, we use inequality
symbols.
 <, ≤, >, ≥,
Real Number Line-Practice
 Use the number lines to graph and order the real
numbers:
 1. 1,5
 2. -2, -3
Real Number Line Practice
 3. -8, 1
 4. - 1 , 2, 3.3
2
Some Practice
 Turn to Part 2 (Classwork Section).
 Complete problems 1- 4. Ask your group members for
help if necessary.
Properties of Real Numbers
 Closure:
 When two real numbers are added, the sum is a real number.
 When two real numbers are multiplied, the product is a real number.
 Commutative:
 When two numbers are added, the sum is the same regardless of the
order of the addends.
 For example 4 + 2 = 2 + 4
 The product is also the same regardless of order.
Example: (2)(4) = (4)(2)
 Associative:
 When three or more numbers are added, the sum is the same regardless
of the grouping of the addends.
 For example (2 + 3) + 4 = 2 + (3 + 4)
 Same with multiplication (except numbers are multiplied not added)
Properties of Real Numbers
 Identity Property: *Trying to keep your given number
 The sum of any number and zero is the original number.
 For example 5 + 0 = 5.
 The multiplication of any number and 1 is the original number.
 Inverse: *Trying to add to zero (additive identity), or multiply to one
(multiplicative identity).
 The sum of any number and its opposite is zero.
 The multiplication of any number and its multiplicative inverse is
one.
 Distributive property:
 The sum of two numbers times a third number is equal to the sum
of each addend times the third number.
 For example 4 * (6 + 3) = 4*6 + 4*3
Identifying Properties
 Identify the property shown:
 (3 + 9) +8 = 3 + (9 + 8)
 14 ∙ 1 = 14
Properties cont.
 The opposite, or additive inverse, of any number a is
–a. The reciprocal, or multiplicative inverse, of any
1
nonzero number a is .a
 Subtraction is defined as adding the opposite, and
division is defined as multiplying by the reciprocal.

a-b = a+-b

ab = a ∙1b, b≠0
Definition of subtraction
Definition of division
Subtraction and Division
Examples
 Rewrite the following using the definition of subtraction
and division:
 The difference of 7 and -10
 The quotient of -24 and
1
3
Unit Analysis
 What units are the final answers in?
 1. 345 miles – 187 miles =
 2. (1.5 hours)(50miles ) =
1hour
Unit Analysis
 3. 24 dollars=
3hours
 4.
88 ft 3600sec 1mile=
(
)(
)(
)
1sec 1hour 5280 ft
Real Life Example: Mexico!
 You are exchanging $400 for Mexican pesos. The
exchange rate is 8.5 pesos per dollar, and the bank
charges a 1% fee to make the exchange.
 How much money should you take to the bank if you
do not want to use part of the $400 to pay the
exchange fee?
Mexico cont.
 B. How much will you receive in pesos?
 C. When you return from Mexico you have 425
pesos left. How much can you get in dollars?
Assume that you use other money to pay the
exchange fee.
Practice
 Turn to Part 2 (Classwork Section).
 Complete problems 5 - 8. Ask your group members for
help if necessary.
 Homework: page 7
 15-21 odd, 27, 28, 33, 34, 61-63 all