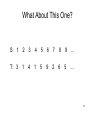Download How Big Is Infinity?

How Big Is Infinity?
Some Mathematical Surprises
Roger House
Scientific Buzz Café
French Garden Restaurant & Bistro
Sebastopol, CA
2013 July 25
Copyright © 2010 Roger House
1
What we're going to talk about
Some infinities are bigger than others.
Sounds weird, but soon it will make sense.
It goes on forever.
There is no “biggest” infinity.
2
Georg Cantor (1845-1918)
•
•
•
•
•
•
Born in St. Petersburg, Russia.
His background: Danish, Catholic,
Jewish, Lutheran.
At the age of 11 Cantor and his family
moved to Germany where he stayed for
the rest of his life.
His entire career was at the Univ. of
Halle.
He invented set theory, the basis of
math.
3
All the ideas we discuss tonight are his.
Finite Sets
•
•
•
•
•
Infinite sets are too hard to think about,
so let's start with finite sets.
But, to make it interesting, imagine we
don't know how to count.
This is not as artificial as it might seem.
Charles Seife says this in Zero: The
Biography of a Dangerous Idea:
“The Siriona Indians of Bolivia and the
Brazilian Yanoama people don't have
words for anything larger than three;
instead, these two tribes use the words
for 'many' or 'much.'”
4
Counting Sheep
•
•
•
•
•
•
Joe has a herd of sheep which he lets
out of a pen each morning into a
pasture.
Each evening the sheep are returned to
the pen.
Joe wants to know if all the sheep which
left in the morning return in the evening.
How can he tell?
Count them.
But what if Joe is a Siriona and cannot 5
count higher than three?
Joe's Solution
•
•
•
As each sheep leaves the pen, Joe puts
a pebble in a bag.
As each sheep returns, Joe removes a
pebble from the bag.
What are the possible outcomes?
–
–
–
•
•
The bag is empty.
There are one or more pebbles in the
bag.
Any other possibilities?
The bag becomes empty before all the
sheep have entered the pen!
Joe quickly adds pebbles to the bag.
6
We Can Use Joe's Solution
•
•
•
•
•
•
Joe has discovered something very
important.
He can keep track of the size of his herd
without knowing how to count.
This is rather astounding; not at all
trivial.
We may be able to count sheep, but we
don't know how to count infinite sets.
We're in the same situation as Joe when
it comes to infinite sets.
So, let's use Joe's idea and apply it to
infinite sets to see “how big” they are.
7
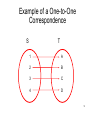
One-to-One Correspondence
•
•
What Joe invented is called a one-toone correspondence (or a bijection):
Given two sets S and T, and a mapping
of elements of S to elements of T, we
call the mapping a one-to-one
correspondence if these conditions hold:
–
–
–
Every element of S is mapped to some
element of T.
Distinct elements of S are mapped to
distinct elements of T.
Every element of T has some element of
S mapped to it.
8
Example of a One-to-One
Correspondence
S
T
1
A
2
B
3
C
4
D
9
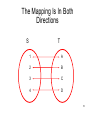
The Mapping Is In Both
Directions
S
T
1
A
2
B
3
C
4
D
10
Another Correspondence
S: 1
2
3
4
5
6
7
8
9
...
T: 2
4
6
8 10 12 14 16 18 ...
11
Yet Another One
S: 1
2
3
4
5
6
7
8
9 …
T: 1
3
5
7
9 11 13 15 17 ...
12
Perhaps More Interesting
S: 1
2
3
4
5
T: 1
4
9 16 25
6
7
8 ...
36 49
64 ...
13
What's This One?
S: 1
2
3
4
5
6
7
8 ...
T: 1
8 27 64 125 216 343 512 ...
14
What About This One?
S: 1
2
3
4
5
6
7
8
9
...
T: 3
1
4
1
5
9
2
6
5
...
15
Cardinality




Did you notice that we've been looking at
correspondences between infinite sets?
We're going to use the idea of a one-toone correspondence to compare the
sizes of sets, infinite as well as finite.
If a one-to-one correspondence exists
between two sets S and T then we say
that S and T have the same cardinality,
denoted S ~ T.
Informally, the cardinality of a set is the
16
size of the set.
Cardinality of Finite Sets





Do {1, 2, 3, 4} and {A, B, C, D, E} have
the same cardinality?
What about {1, 2, 3, 4} and {A, B, C}?
{1, 2, 3, 4} and {A, B, C, D}?
For any finite set, just count the
elements to determine the cardinality.
If there are 7 elements, then, when you
finish counting, you have a one-to-one
correspondence between the elements
of the set and the elements of {1, 2, 3, 4,
5, 6, 7}.
17
The Natural Numbers

Our favorite infinite set is  = {1, 2, 3,
...}, the set of natural numbers, also
called:
—
—
—
counting numbers
positive whole numbers
positive integers
•
We use the natural numbers to
investigate the size of infinite sets.
•
By the way, are we sure that  is
infinite?
18
Countable Sets



If a set S is finite, or if it has the same
size as  (i.e., there is a one-to-one
correspondence between S and ), then
the set is said to be countable.
In other words, you can count the members of a countable set.
The term denumerable is also used; it
means the same as countable.
19
Same-Size Sets

So far, we've seen that all the following
sets have the same cardinality (i.e., the
same “size”) as the natural numbers :
–
–
–
–

even natural numbers
odd natural numbers
squares of natural numbers
cubes of natural numbers
All of the above are subsets of ; let's go
for something bigger than .
20
~Z
What does this correspondence show?
… 8
6
4
2 1 3 5 7 9 ...
… -4
-3 -2 -1 0 1 2 3 4 …
This is a one-to-one correspondence
between the natural numbers  and the
integers Z, so Z is countable.
21
The Rational Numbers Q


Consider numbers of the form n/d,
where both n and d are integers, i.e.,
whole numbers.
Some examples:
—
—


1/2, 2/3, 4/1, 1001/57, -3/2, 1000000/18
1/1, 2/1, 3/1, 4/1, 5/1, ...
These numbers are called rational
because they are ratios of integers.
Note that  is a subset of Z, and Z is a
subset of Q.
22
Counting Numbers

Consider the interval [-2, 2]:
--|------------|------------|------------|------------|--2
-1
0
1
2



How many integers are in this interval?
How many natural numbers?
How many rational numbers?
23
The Rationals Are Dense

Consider the interval [0, 1]:
--|--------------------------------------------------|-0
1



How many rationals are in this interval?
Lots and lots and lots.
The rationals are dense: Between any
two of them there is another one.
24
Are the Rationals Countable?





Claim: The set of rational numbers is
countable.
Do you believe this?
Any ideas on how to show that it is true
or not true?
To prove it true, we need to come up
with a one-to-one correspondence
between the rationals and the natural
numbers.
Does this mean we need to find a
smallest rational number?
25
Any Positive Rationals Missing?
1:
2:
3:
4:
5:
6:
7:
…
1
1/1
2/1
3/1
4/1
5/1
6/1
7/1
…
2
½
2/2
3/2
4/2
5/2
6/2
7/2
…
3
1/3
2/3
3/3
4/3
5/3
6/3
7/3
…
4
¼
2/4
3/4
4/4
5/4
6/4
7/4
…
5
1/5
2/5
3/5
4/5
5/5
6/5
7/5
…
6
1/6
2/6
3/6
4/6
5/6
6/6
7/6
…
7
1/7
2/7
3/7
4/7
5/7
6/7
7/7
…
...
...
...
...
...
...
…
…
26
Which Numbers Are Gone?
1:
2:
3:
4:
5:
6:
7:
…
1
1/1
2/1
3/1
4/1
5/1
6/1
7/1
…
2
½
3/2
5/2
7/2
…
3
1/3
2/3
4
¼
5
6
7
1/5 1/6 1/7 ...
2/5
2/7 ...
3/4 3/5
3/7 ...
4/3
4/5
4/7 ...
5/3 5/4
5/6 5/7 ...
6/5
6/7 ...
7/3 7/4 7/5 7/6
…
… … … … … …
27
The Rationals Are Countable
1:
2:
3:
4:
5:
6:
7:
…
1
1/1
2/1
3/1
4/1
5/1
6/1
7/1
…
2
½
3/2
5/2
7/2
…
3
1/3
2/3
4
¼
5
6
7
1/5 1/6 1/7 ...
2/5
2/7 ...
3/4 3/5
3/7 ...
4/3
4/5
4/7 ...
5/3 5/4
5/6 5/7 ...
6/5
6/7 ...
7/3 7/4 7/5 7/6
…
… … … … … …
28
The Rationals Are Countable
1
2
3
4
5
6
7
8
9
10
–
–
–
–
–
–
–
–
–
–
1
1/2
2
3
1/3
1/4
2/3
3/2
4
5
11
12
13
14
15
16
17
18
19
20
–
–
–
–
–
–
–
–
–
–
1/5
1/6
2/5
3/4
4/3
5/2
6
7
5/3
3/5
29
The Rationals Are Countable





At this point you should be stunned.
The rationals are dense; between any
two distinct rationals there is another
rational.
In fact, between any two distinct
rationals there are an infinite number of
rationals.
The rationals seem to completely fill the
number line; the integers appear with
gaps between them.
And yet, there are no more rationals
than there are integers.
30
Maybe All Sets Are Countable?






 is countable.
Every subset of  is countable.
The superset Z of  is countable.
The superset Q of  is countable.
What else is there?
Might a set exist which is “bigger” than
?
31
The Power Set of 





Let S be the set of all subsets of .
Technical term: S is the power set of .
Note that the members of S are not
natural numbers.
The members of S are sets of natural
numbers.
Name a few members of S.
32
Some Members of S








The set of even natural numbers.
The set of odd natural numbers.
The set of squares of natural numbers.
The set of cubes of natural numbers.
The sets {1}, {2}, {3}, ..., {n}, …
The sets {1,2}, {2,3}, {3,4}, ..., {n,n+1}, …
The sets {1,2,3}, {2,3,4}, {3,4,5}, …
{n,n+1,n+2}, …
Are there any more?
33
Naming Members of S
: 1
S1: 0
S2: 1
S3: 1
S4: 1
S5: 1
S6: 0
S7: 0
S8: 1
2
1
0
0
0
0
1
0
1
3
0
1
0
0
0
0
1
0
4
1
0
1
0
0
0
0
0
5
0
1
0
0
0
0
0
0
6
1
0
0
0
0
0
0
0
7
0
1
0
0
0
0
0
0
8
1
0
0
1
0
0
0
0
9 10 11 12 13 …
0 1 0 1 0…
1 0 1 0 1…
1 0 0 0 0…
0 0 0 0 0…
0 0 0 0 0…
0 0 0 0 0…
0 0 0 0 0…
0 0 0 0 0…
34
It's all 0's and 1's




Note that every sequence of 0's and 1's
describes a unique subset of .
Note that every subset of  can be
described uniquely as a sequence of 0's
and 1's.
So, what have we got?
A one-to-one correspondence between
the set of subsets of  and the set of
sequences of 0's and 1's.
35
Let's Make an Assumption



So, the set of all subsets of  and the
set of all sequences of 0's and 1's have
the same cardinality; these two sets are
the same size.
Can these sets be put in a one-to-one
correspondence with ?
Assume this is the case, and consider
any one-to-one correspondence
between  and the set of sequences of
0's and 1's.
36
A 1-to-1 Correspondence
1: 0 1 0 1 0 1 0 1 0 1 0 1
2: 1 0 1 0 1 0 1 0 1 0 1 0
3: 1 0 1 1 0 0 0 0 1 0 0 0
4: 1 0 0 0 0 0 0 1 0 0 0 0
5: 1 0 0 0 1 0 0 0 0 0 0 0
6: 0 1 0 0 0 0 0 0 0 0 0 0
…
Note that this list goes on forever.
0…
1…
0…
0…
0…
0…
37
So, What Do We Have?
•
For every natural number n we have a
unique sequence of 0's and 1's.
•
In principle, we can list all the
sequences.
•
Also, there are no sequences of 0's and
1's which are not in the list because we
have a one-to-one correspondence.
38
•
However, there is a little problem ...
Another Member of S
1:
2:
3:
4:
5:
6:
0
1
1
1
1
0
1
0
0
0
0
1
0
1
1
0
0
0
1
0
1
0
0
0
0
1
0
0
1
0
1
0
0
0
0
0
0
1
0
0
0
0
1
0
0
1
0
0
0
1
1
0
0
0
x: 1 1 0 1 0 1 - - -
1
0
0
0
0
0
0
1
0
0
0
0
- -
1
0
0
0
0
0
0…
1…
0…
0…
0…
0…
- - …
39
Prelude to a Contradiction




Is the sequence x a member of the set of
all sequences of 0's and 1's?
Of course. Look at it. It's a sequence of
0's and 1's, so it must be in the set of all
sequences of 0's and 1's.
Is there some natural number n that
corresponds to x in the given one-to-one
correspondence?
There must be, because otherwise we
wouldn't have a one-to-one
40
correspondence.
A Contradiction




We have a little problem here: Which
natural number n corresponds to x?
We defined x in such a way that it differs
from EVERY sequence in the
correspondence in at least one place.
So we have arrived at a contradiction: x
must correspond to some natural
number, but x doesn't correspond to any
natural number.
What's wrong? How did we get into this
mess?
41
A Way Out of the Mess




We made an assumption, namely that a
one-to-one correspondence exists
between the set of all sequences of 0's
and 1's and the set .
This assumption led to a contradiction.
Which means the assumption is false.
So there does not exist a one-to-one
correspondence between  and the set
of all sequences of 0's and 1's.
42
The Grand Conclusion Is ...




There is always at least one sequence of
0's and 1's which does not correspond to
any natural number.
So the set of sequences of 0's and 1's is
bigger than .
Recall that the set of all 0's and 1's is the
same size as S, the set of all subsets of
.
So S is bigger than .
43
Are You Stunned Yet?




If you weren't stunned to see that the
rational numbers are countable, it's now
time to be stunned.
What you have just seen is a proof that
some infinities are bigger than others.
There are more sets of natural numbers
than there are natural numbers.
In fact, the cardinality of S is *way*
bigger than the cardinality of .
44
Don't Stop Now



Let T be the set of all subsets of S.
Remember that members of S are
subsets of .
A member of T:
–

Another member of T:
–

{ {odd numbers}, {square numbers} }
{ {1}, {2, 10}, {primes} }
How does the size of T compare to the
size of S?
45
, S, T, U, ...





The size of T is way bigger than the
size of S.
Remember that the size of S is way
bigger than the size of .
So, T is way, way bigger than .
Now let U be the set of all subsets of T.
What is your guess about the size of U
compared to the size of T?
46
It Just Keeps Going On and On
and On ...






You guessed right: The size of U is
bigger than the size of T.
Here's the scary part: It goes on forever.
Given any set X, let Y be the set of all
subsets of X. Then Y is a bigger set
than X.
There is no largest infinity.
Given any infinite set we can easily
construct a larger infinite set.
It just keeps going on and on and on ...
47
What we have seen

The two main points of this talk:
—
—


Don't feel bad if these results leave you
with an uneasy feeling.
Here is what Cantor had to say about
one of his own results:
—

Some infinities are bigger than others.
There is no biggest infinity.
"I see it, but I don't believe it!"
Mathematics is full of surprises.
48
David Hilbert On Cantor's Work
David Hilbert (1862-1943) on Cantor's work
on set theory:
"The finest product of mathematical genius
and one of the supreme achievements of
purely intellectual human activity."
“No one will expel us from this paradise
Cantor has created for us.”
49