* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Brief introduction to quantum mechanics
Lattice Boltzmann methods wikipedia , lookup
Scalar field theory wikipedia , lookup
Bell's theorem wikipedia , lookup
Quantum entanglement wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Coherent states wikipedia , lookup
Ensemble interpretation wikipedia , lookup
Quantum teleportation wikipedia , lookup
Quantum state wikipedia , lookup
Hydrogen atom wikipedia , lookup
Wheeler's delayed choice experiment wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Renormalization wikipedia , lookup
History of quantum field theory wikipedia , lookup
Renormalization group wikipedia , lookup
EPR paradox wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Path integral formulation wikipedia , lookup
Probability amplitude wikipedia , lookup
Hidden variable theory wikipedia , lookup
Dirac equation wikipedia , lookup
Schrödinger equation wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Canonical quantization wikipedia , lookup
Identical particles wikipedia , lookup
Electron scattering wikipedia , lookup
Atomic theory wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Elementary particle wikipedia , lookup
Particle in a box wikipedia , lookup
Wave function wikipedia , lookup
Double-slit experiment wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Wave–particle duality wikipedia , lookup
Matter wave wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
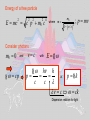
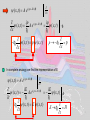
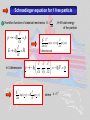
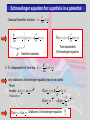
A very elementary approach to Quantum mechanics „There was a time when newspapers said that only twelve men understood the theory of relativity. I do not believe that there ever was such a time... On the other hand, I think it is safe to say that no one understands quantum mechanics“ R.P. Feynman The Character of Physical Law (1967) let´s approach some aspects of qm anyway Experimental facts: Light has wave (interference) and particle properties Ekin max Plot from Radiation modes in a hot cavity provide a test of quantum theory Existence of photons E Frequency Planck’s const. Energy of the quantum Energy of a free particle E mc c p m0 c 2 2 2 4 where m 2 m0 1 v / c 2 ; p mv Consider photons m0 0 cp and vc with E h h p k or p c c c ck Dispersion relation for light Electrons (particles) have wave properties Figures from p k applicable for “particles” de Broglie Today: LowEenergyElectronDiffraction standard method in surface science LEED Fe0.5Zn0.5F2(110) 232 eV top view (110)-surface Implications of the experimental facts Electrons described by waves: ( x, t ) A ei ( kxt ) ( x, t )dx ( x, t ) ( x, t )dx ( x, t ) dx 2 * Wave function (complex for charged particles like electrons) Probability to find electron at (x,t) Which equation describes the temporal evolution of ( x, t ) Schroedinger equation Can’t be derived, but can be made plausible Let’s start from the wave nature of, e.g., an electron: Erwin Schroedinger ( x, t ) A ei ( kxt ) and take advantage of p k ;E ( x, t ) A e x i ( px Et ) / ip ip ( x, t ) A ei ( px Et ) / ( x, t ) x i ( x, t ) p ( x, t ) x p i i p x In complete analogy we find the representation of E ( x, t ) A ei ( px Et ) / t iE iE i ( px Et ) / ( x, t ) A e ( x, t ) i t i ( x, t ) E ( x, t ) E i H t t Schroedinger equation for 1 free particle p2 Hamilton function of classical mechanics H 2m p x E i H t p i In 3 dimensions 2 2m ; H=E total energy of the particle 2 ( x , t ) i ( x, t ) 2 2m x t 2 1-dimensional p i , , i p x y z ( r , t ) i (r , t) t 2 where Schroedinger equation for a particle in a potential Classical Hamilton function: H p2 2m V (r ) H ( r , t ) i (r , t) t 2 V ( r ) ( r , t ) i (r , t) 2 m t H Time dependent Schroedinger equation Hamilton operator If H independent of time like H 2 2m V (r ) only stationary Schroedinger equation has to be solved Proof: i Et ( r , t ) ( r ) e H ( r , t ) i (r , t) Ansatz: (Trial function) H ( r ) e i Et t i Et i (r ) e t H ( r ) E ( r ) Stationary Schroedinger equation Solving the Schroedinger equation (Eigenvalue problem) Solution requires: -Normalization of the wave function according (r ) d 3r 1 2 Physical meaning: probability to find the particle somewhere in the universe is 1 -Boundary conditions of the solution: and have to be continuous when merging piecewise solutions Note: boundary conditions give rise to the quantization Particle in a box: 2 nx sin L L n ( x) En 2 n2 2 2 2mL Eigenfunctions n 1, 2,3,... Eigenenergies Quantum number x Details see homework Heisenberg‘s uncertainty principle It all comes down to the wave nature of particles ( x, t ) A ei ( px Et ) / Wave function given by a single wavelength p h Momentum p precisely known, but where is the particle position -P precisely given -x completely unknown Wave package p1 h 1 p2 h 2 Fourier-analysis Particle somewhere in the region x Particle position known with uncertainty x x p Particle momentum known with uncertainty p In analogy 2 Fourier-theorem E t 2