* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 22: Electromagnetic Waves
First observation of gravitational waves wikipedia , lookup
Electrostatics wikipedia , lookup
Electromagnet wikipedia , lookup
Field (physics) wikipedia , lookup
Faster-than-light wikipedia , lookup
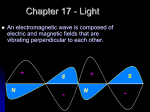
Superconductivity wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Magnetic monopole wikipedia , lookup
Diffraction wikipedia , lookup
Circular dichroism wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Lorentz force wikipedia , lookup
Speed of gravity wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electromagnetism wikipedia , lookup
Time in physics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
My Chapter 22 Lecture 1 Chapter 22: Electromagnetic Waves •Production of EM waves •Maxwell’s Equations •Antennae •The EM Spectrum •Speed of EM Waves •Doppler Effect 2 §22.1 Maxwell’s Equations and EM Waves A stationary charge produces an electric field. A charge moving at constant speed produces electric and magnetic fields. 3 A charge that is accelerated will produce variable electric and magnetic fields. These are electromagnetic (EM) waves. If the charge oscillates with a frequency f, then the resulting EM wave will have a frequency f. If the charge ceases to oscillate, then the EM wave is a pulse (a finitesized wave). 4 Faraday’s Law: A changing magnetic field creates an electric field. Ampère-Maxwell Law A current or a changing electric field creates a magnetic field. 5 When Maxwell’s equations are combined, the solutions are electric and magnetic fields that vary with position and time. These are EM waves. An electric field only wave cannot exist, nor can a magnetic field only wave. 6 §22.2 Antennae An electric field parallel to an antenna (electric dipole) will “shake” electrons and produce an AC current. 7 An EM wave also has a magnetic component. A magnetic dipole antenna can be oriented so that the B-field passes into and out of the plane of a loop, inducing a current in the loop. The B-field of an EM wave is perpendicular to its E-field and also the direction of travel. 8 §22.3 The EM Spectrum EM waves of any frequency can exist. 9 The EM Spectrum: Energy increases with increasing frequency. 10 §22.4 Speed of Light Maxwell was able to derive the speed of EM waves in vacuum. EM waves do not need a medium to travel through. c 1 0 0 8.85 10 1 12 C 2 /Nm 2 4 10 7 Tm/A 3.00 108 m/s 11 In 1675 Ole Römer presented a calculation of the speed of light. He used the time between eclipses of Jupiter’s Gallilean Satellites to show that the speed of light was finite and that its value was 2.25108 m/s. Fizeau’s experiment of 1849 measured the value to be about 3108 m/s. (done before Maxwell’s work) 12 When light travels though a material medium, its speed is reduced. c v n where v is the speed of light in the medium and n is the refractive index of the medium. When a wave passes from one medium to another the frequency stays the same, but the wavelength is changed. A dispersive medium is one in which the index of refraction depends on the wavelength of light. 13 Example (text problem 22.22): In order to study the structure of a crystalline solid, you want to illuminate it with EM radiation whose wavelength is the same as the spacing of the atoms in the crystal (0.20 nm). (a) What is the frequency of the EM radiation? 3.0 108 m/s 15 f 1 . 5 10 Hz 9 0.20 10 m c (b) In what part of the EM spectrum does it lie? X-ray 14 §22.5 Properties of EM Waves All EM waves in vacuum travel at the “speed of light” c. Both the electric and magnetic fields have the same oscillation frequency f. The electric and magnetic fields oscillate in phase. 15 The fields are related by the relationship E ( x, y, z, t ) cB( x, y, z, t ) EM waves are transverse. The fields oscillate in a direction that is perpendicular to the wave’s direction of travel. The fields are also perpendicular to each other. 16 The direction of propagation is given by E B. The wave carries one-half of its energy in its electric field and one-half in its magnetic field. 17 §22.8 The Doppler Effect For EM waves, the Doppler shift formula is fo f s v c v 1 c 1 where fs is the frequency emitted by the source, fo is the frequency received by the observer, v is the relative velocity of the source and the observer, and c is the speed of light. 18 If the source and observer are approaching each other, then v is positive, and v is negative if they are receding. When v/c << 1, the previous expression can be approximated as: v f o f s 1 c 19 Example (text problem 22.56): Light of wavelength 659.6 nm is emitted by a star. The wavelength of this light as measured on Earth is 661.1 nm. How fast is the star moving with respect to the Earth? Is it moving toward Earth or away from it? The wavelength shift is small ( << ) so v << c. v f o f s 1 c c / o s v fo 1 1 1 0.0023 c fs c / s o v 6.8 105 m/s 680 km/s Star is receding. 20 Summary •Maxwell’s Equations •Electric and Magnetic Dipole Antennae •EM Spectrum •Properties of EM Waves •Doppler Effect 21