Download BEC 2 - JILA

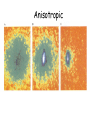
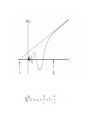
• Brief overview of dilute ultra-cold gases
• Quantum dynamics of atomic matter waves
• The Bose Hubbard and Hubbard models
High temperature T:
Thermal velocity v
Density d-3
“billiard balls”
Low temperature T:
De Broglie wavelength
lDB=h/mv~T-1/2
“Wave packets”
T=Tcrit : Bose Einstein Condensation
De Broglie wavelength
lDB=d
“Matter wave overlap”
T=0 : Pure Bose Einstein Condensate
“Giant matter wave ”
Ketterle
In 1995 (70 years after Einstein’s prediction) teams in Colorado and
Massachusetts achieved BEC in super-cold gas.This feat earned
those scientists the 2001 Nobel Prize in physics.
S. Bose, 1924
Light
A. Einstein, 1925
Atoms
E. Cornell
C. Wieman
W. Ketterle
Using Rb and Na atoms
At T<Tf ~Tc fermions form a degenerate Fermi gas
ℏ2
𝐸𝐹 ~
3𝜋 2 𝑛
2𝑚
1999: 40 K JILA, Debbie Jin group
2/3
An atom with velocity V is illuminated with a laser with appropriate frequency
Trapping and cooling: MOT
laser
Atom
To cool the
atoms down we need to
apply lasers in all three directions
Atoms absorb light and reduce their speed
Laser cooling is not enough to cool
down the atoms to quantum degeneracy
and other tecniques are required
Slower atom
As the atoms slow down the gas is cooled down
Temperatures down to 10-100 nanoK
Each atom behaves as a bar magnet
This process is similar to what happens with your cup
of coffee.
The hottest molecules escape from the cup as vapor
In a magnetic field atoms can be trapped:
magnetic field~coffee cup
By changing the magnetic field the hot
atoms escape and only the ones that are
cold enough remain trapped
BEC
2001
Time of flight images
t=0 Turn off trapping potentials
Light Probe
Image
T>Tc
T<Tc
T=Tc
MPI,Munich
Anisotropic
(1) Particles behave like waves (T → 0)
ℏ2 2
− 𝛻 Ψ
2𝜇
+ 𝑉(𝑟) Ψ=EΨ
There is only a phase shift at long range!!
Phase shift at low energy proportional to
“scattering length”
𝑎
Characterizes low energy collisions
Goal: find scattered wave
∝
(r) =
𝑒 𝑖𝑘𝑧
f: scattering amplitude
𝑒 𝑖𝑘𝑟
+ 𝑓(Ω)
𝑟
ℓ 𝑅ℓ (𝑟, 𝐸)𝑃ℓ (cos 𝜃).
l = 0, 1, 2… s-, p-, waves, …
1
𝜋
𝑅ℓ (𝑟 → ∞) → sin 𝑘𝑟 − ℓ − 𝛿ℓ
𝑘𝑟
2
There is only a phase
shift at long range!!
cross section
atoms/s scattered flux into d
plane wave flux (atoms/cm2/s)
Solve Schrödinger equation for each l
𝛿ℓ
Get phase shift
𝛿ℓ
→ 𝐴ℓ (𝐴ℓ 𝑘) 2ℓ
𝑘
𝐴0 =a
Quantum statistics matter
Pauli Exclusion principle
𝛿ℓ
𝑘→0
“scattering length”
𝐴1 =b3 “scattering volume ”
Identical bosons: even
Identical fermions: odd
Non-identical species: all
Characterize s-wave collisions
Characterize p-wave collisions
• Two interaction potentials V and V’ are equivalent if they have
the same scattering length
• So: after measuring a for the real system, we can model with a
very simple potential.
• Actually, to avoid divergences you need
Huang and Yang, Phys. Rev. 105,
767 (1957)
Also E. Fermi (1936), Breit (1947),
Blatt and Weisskopf (1952)
• Quantum phenomena on a macroscopic scale.
•Ultra cold gases are dilute
a: Scattering Length
n: Density
Eint .
an
 2 2 / 3  man1 / 3 ~ 0.1  1
 n
Ekin
2m
Cold gases have almost 100% condensate fraction.
In contrast to other superfluids like liquid Helium which have
at most 10%
Field operator
ˆ (r ), 
ˆ t (r ' )]   (r  r ' )
[
Many body Hamiltonian
Equation of Motion
In general
Ψ′ =0
Dilute ultracold bosonic atoms are easy to model
1. Short range interactions
2. At T=0 all share the same macroscopic wave
function
ΨΦ =ΦΦ
Gross-Pitaevskii Equation
We can understand the many-body system by a single
non linear equation
A BEC is a coherent collection of
atomic deBroglie waves
laser light is a coherent collection
of electromagnetic waves
laser
Vortices
Coherence
JILA 2002
MIT (1997).
Weakly
interacting
Bose Gas
Superflow
Non
Linear
optics
MIT (1997).
NIST (1999).