Download Subrecursive Sum Approximations of Irrational Numbers

Welcome!
Subrecursive Sum Approximations of
Irrational Numbers
Lars Kristiansen
Department of Mathematics, University of Oslo
Department of Informatics, University of Oslo
Introduction
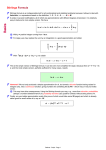
A function C : N → Q is a Cauchy sequence for the real number α
when
1
|α − C (n)| < n .
2
A function C : N → Q is a Cauchy sequence for the real number α
when
1
|α − C (n)| < n .
2
A function E : N → Z is the base-2 expansion of the real number
α when
E (n) ∈ {0, 1} for n ≥ 1
∞
X
E (i)
α = E (0) +
2i
i=1
A function C : N → Q is a Cauchy sequence for the real number α
when
1
|α − C (n)| < n .
2
A function E : N → Z is the base-2 expansion of the real number
α when
E (n) ∈ {0, 1} for n ≥ 1
∞
X
E (i)
α = E (0) +
2i
i=1
A function D : Q → {0, 1} is a Dedekind cut for the real number α
when
D(q) = 0 iff q < α .
A Cauchy sequence can be subrecursively computed in a base-2
expansion, but. . .
we cannot turn a Cauchy sequence into a base-2
expansion by subrecursive means; this requires
unbounded search, that is, full Turing computability.
A Cauchy sequence can be subrecursively computed in a base-2
expansion, but. . .
we cannot turn a Cauchy sequence into a base-2
expansion by subrecursive means; this requires
unbounded search, that is, full Turing computability.
A base-2 expansion can be subrecursively computed in a Dedekind
cut, but. . .
we cannot turn a base-2 expansion into a Dedekind cut
by subrecursive means. This requires unbounded search,
that is, full Turing computability.
Thus, it makes perfectly good sense to talk about three different
levels of subrecursive representability of irrational numbers: the
D-level, the E -level and the C -level.
For any class of functions S
let SC denote the set of irrational numbers that have a
Cauchy sequence in S
let S2E denote the set of irrational numbers that have a
base-2 expansion in S
let SD denote the set of irrational numbers that have a
Dedekind cut in S.
Definition: A class of function is subrecursive if it is contained in
an efficiently enumerable class of computable total functions.
Definition: A class of function is subrecursive if it is contained in
an efficiently enumerable class of computable total functions.
Theorem: For any subrecursive class S which is closed under
Kalmar elementary operations, we have
SD ⊂ S2E ⊂ SC .
Sum Approximations
Any irrational number α can be written of the form
α = a +
1
1
1
+ k + k + ...
k
0
1
2
2
22
where k0 , k1 , k2 , . . . is a strictly monotone increasing sequence of
natural numbers and a is an integer.
Any irrational number α can be written of the form
α = a +
1
1
1
+ k + k + ...
k
0
1
2
2
22
where k0 , k1 , k2 , . . . is a strictly monotone increasing sequence of
natural numbers and a is an integer.
Any irrational number α can be written of the form
α = a −
1
1
1
− k − k − ...
2k0
21
22
where k0 , k1 , k2 , . . . is a strictly monotone increasing sequence of
natural numbers and a is an integer.
Let A : N → N be a strictly monotone function. We will say that A
is a sum approximation from below of the the real number α if
there exists a ∈ Z such that
α = a +
∞
X
i=0
1
2A(i)+1
.
Let A : N → N be a strictly monotone function. We will say that A
is a sum approximation from above of the the real number α if
there exists a ∈ Z such that
α = a −
∞
X
i=0
1
2A(i)+1
.
Let S↑ denote the set of irrational numbers that have sum
approximations from below in the subrecursive class S.
Let S↓ denote the set of irrational numbers that have sum
approximations from above in the subrecursive class S.
Then, we have
Let S↑ denote the set of irrational numbers that have sum
approximations from below in the subrecursive class S.
Let S↓ denote the set of irrational numbers that have sum
approximations from above in the subrecursive class S.
Then, we have
S↑ 6⊆ S↓
and
S↓ 6⊆ S↑ .
Let S↑ denote the set of irrational numbers that have sum
approximations from below in the subrecursive class S.
Let S↓ denote the set of irrational numbers that have sum
approximations from above in the subrecursive class S.
Then, we have
S↑ 6⊆ S↓
and
S↓ 6⊆ S↑ .
To put it slightly different: the ↑-level and the ↓-level are
incomparable levels.
Note that it follows that
S↑ ⊂ S2E
(strict inclusions).
and
S↓ ⊂ S2E
Note that it follows that
S↑ ⊂ S2E
and
S↓ ⊂ S2E
and
S↓ ⊆ S2E .
(strict inclusions).
It is obvious that we have
S↑ ⊆ S2E
and we cannot have S↑ = S2E or S↓ = S2E because that
contradicts that S↑ and S↓ are incomparable.
Let us discuss the proof of
S↑ 6⊆ S↓
(The proof of S↓ 6⊆ S↑ is symmetric.)
Note that an irrational number has one, and only one, sum
approximation from below . . .
Note that an irrational number has one, and only one, sum
approximation from below . . . and one, and only one, sum
approximation from above.
Note that an irrational number has one, and only one, sum
approximation from below . . . and one, and only one, sum
approximation from above.
Thus if  increases to fast to be in S, then
α = 0 +
will not be in S↑ .
∞
X
1
i=0
2Â(i)+1
Note that an irrational number has one, and only one, sum
approximation from below . . . and one, and only one, sum
approximation from above.
Thus if  increases to fast to be in S, then
α = 0 +
∞
X
1
i=0
2Â(i)+1
will not be in S↑ .
But the sum approximation of α from above might very well be in
S.
Note that an irrational number has one, and only one, sum
approximation from below . . . and one, and only one, sum
approximation from above.
Thus if  increases to fast to be in S, then
α = 0 +
∞
X
1
i=0
2Â(i)+1
will not be in S↑ .
But the sum approximation of α from above might very well be in
S.
Indeed, if the approximation from below is a fast-growing function,
the approximation from above will be a slow-growing function.
Let
α
=
0 +
∞
X
1
i=0
2Â(i)+1
=
1 −
∞
X
1
i=0
2Ǎ(i)+1
.
Let
α
=
0 +
If
∞
X
1
i=0
2Â(i)+1
=
1 −
∞
X
1
i=0
2Ǎ(i)+1
1
1
1
1
+ 5 + 17 + 100 + . . .
3
2
2
2
2
is the approximation from below, then
α = 0 +
.
Let
α
=
0 +
∞
X
1
i=0
2Â(i)+1
=
1 −
∞
X
1
i=0
2Ǎ(i)+1
.
If
1
1
1
1
+ 5 + 17 + 100 + . . .
3
2
2
2
2
is the approximation from below, then
α = 0 +
α = 1−
1
1
1
1
1
1
1
− 2 − 4 − 6 − 7 − 8 − 9 − ...
1
2
2
2
2
2
2
2
is the approximation from above.
Let
α
=
0 +
∞
X
1
i=0
2Â(i)+1
=
1 −
∞
X
1
i=0
2Ǎ(i)+1
.
If
1
1
1
1
+ 5 + 17 + 100 + . . .
3
2
2
2
2
is the approximation from below, then
α = 0 +
α = 1−
1
1
1
1
1
1
1
− 2 − 4 − 6 − 7 − 8 − 9 − ...
1
2
2
2
2
2
2
2
is the approximation from above.
In general
rng(Ǎ) = N \ rng(Â) .
Let S be an subrecursive class closed under Kalmar elementary
operations.
Let S be an subrecursive class closed under Kalmar elementary
operations.
Let f be an honest function that increases to fast to be in S.
Let S be an subrecursive class closed under Kalmar elementary
operations.
Let f be an honest function that increases to fast to be in S.
Let
α
=
0 +
∞
X
i=0
Then
1
2f (i)+1
.
Let S be an subrecursive class closed under Kalmar elementary
operations.
Let f be an honest function that increases to fast to be in S.
Let
α
=
0 +
∞
X
i=0
1
2f (i)+1
.
Then
α does not have a sum approximation from below in S
Let S be an subrecursive class closed under Kalmar elementary
operations.
Let f be an honest function that increases to fast to be in S.
Let
α
=
0 +
∞
X
i=0
1
2f (i)+1
.
Then
α does not have a sum approximation from below in S
α has a sum approximation from above in S
Let S be an subrecursive class closed under Kalmar elementary
operations.
Let f be an honest function that increases to fast to be in S.
Let
α
=
0 +
∞
X
i=0
1
2f (i)+1
.
Then
α does not have a sum approximation from below in S
α has a sum approximation from above in S
moreover, the Dedekind cut of α is in S.
Thus, we conclude that
S↑ 6⊆ S↓
and
S↑ 6⊆ SD .
Thus, we conclude that
S↑ 6⊆ S↓
and
S↑ 6⊆ SD .
and
S↓ 6⊆ SD .
A symmetric argument yields
S↓ 6⊆ S↑
Moreover, by diagonalisation, we can construct α, β and γ such
that
α, β, γ 6∈ SD
and
α ∈ S↑ ∩ S↓
β ∈ S↑ \ S↓
γ ∈ S↓ \ S↑ .
Moreover, by diagonalisation, we can construct α, β and γ such
that
α, β, γ 6∈ SD
and
α ∈ S↑ ∩ S↓
β ∈ S↑ \ S↓
γ ∈ S↓ \ S↑ .
The constructions of the three numbers are similar, and I would
say that they all are standard diagonalisation constructions.
Moreover, by diagonalisation, we can construct α, β and γ such
that
α, β, γ 6∈ SD
and
α ∈ S↑ ∩ S↓
β ∈ S↑ \ S↓
γ ∈ S↓ \ S↑ .
The constructions of the three numbers are similar, and I would
say that they all are standard diagonalisation constructions.
Let us look at a Venn diagram.
VENN DIAGRAM I
Sum Approximations in Different Bases
The sum approximations discussed above can be considered as sum
approximations in base 2.
The sum approximations discussed above can be considered as sum
approximations in base 2.
In general, we can sum-approximate irrational numbers α in any
base b ≥ 2.
The sum approximations discussed above can be considered as sum
approximations in base 2.
In general, we can sum-approximate irrational numbers α in any
base b ≥ 2.
We can write an irrational number α of the form
α = a +
d0
d1
d2
+ k + k + ...
b k0
b 1
b 2
(from below)
where k0 , k1 , k2 , . . . is a strictly monotone increasing sequence of
natural numbers and a is an integer and di ∈ {1, . . . , b − 1}.
and of the form
α = a −
d0
d1
d2
− k − k − ...
k
0
1
b
b
b 2
(from above)
where k0 , k1 , k2 , . . . is a strictly monotone increasing sequence of
natural numbers and a is an integer and di ∈ {1, . . . , b − 1}.
The computational complexity of a sum approximation depends
significantly on the base.
The computational complexity of a sum approximation depends
significantly on the base.
For natural numbers a, b ≥ 2, we define the relation by
ab
⇔
every factor of a is also a factor of b .
The computational complexity of a sum approximation depends
significantly on the base.
For natural numbers a, b ≥ 2, we define the relation by
ab
⇔
every factor of a is also a factor of b .
Let Sb↑ denote the set of irrational numbers that have a base-b
sum approximation (from below) in the subrecursive class S.
The computational complexity of a sum approximation depends
significantly on the base.
For natural numbers a, b ≥ 2, we define the relation by
ab
⇔
every factor of a is also a factor of b .
Let Sb↑ denote the set of irrational numbers that have a base-b
sum approximation (from below) in the subrecursive class S.
For any S closed under primitive recursive operations we have
ab
⇔
Sb↑ ⊆ Sa↑ .
Thus we have, e.g.
S2↑ 6⊆ S3↓
and
S3↓ 6⊆ S2↑
S10↑ ⊂ S2↑
Thus we have, e.g.
S2↑ 6⊆ S3↓
and
S3↓ 6⊆ S2↑
S10↑ ⊂ S2↑
S6↑ ⊆ S2↑ ∩ S3↑
Thus we have, e.g.
S2↑ 6⊆ S3↓
and
S3↓ 6⊆ S2↑
S10↑ ⊂ S2↑
S6↑ ⊆ S2↑ ∩ S3↑
S2↑ = S4↑ = S8↑ = . . . = S2n ↑ = . . .
The corresponding equivalence holds for base-b expansions:
Let SbE denote the set of irrational numbers that have a base-b
expansion in S. For any S closed under elementary operations we
have
a b ⇔ SbE ⊆ SaE .
The corresponding equivalence holds for base-b expansions:
Let SbE denote the set of irrational numbers that have a base-b
expansion in S. For any S closed under elementary operations we
have
a b ⇔ SbE ⊆ SaE .
The implication from left-right was proved in a paper of Mostowski
(1957). The right-left implication is posed as an open problem in
the same paper.
General Sum Approximations
The formal definition of a general sum approximation may be hard
to digest, but it is really straightforward . . . here it comes:
Let G : N × N → Q be such that, for each b > 1, we have
G (b, i) =
di
b ki
where di ∈ {1, . . . , b − 1} and ki ∈ N and 0 < ki < ki+1 (for all
i ∈ N).
Let G : N × N → Q be such that, for each b > 1, we have
G (b, i) =
di
b ki
where di ∈ {1, . . . , b − 1} and ki ∈ N and 0 < ki < ki+1 (for all
i ∈ N).
We say that G is a general sum approximation from below of the
the real number α if there exists a ∈ Z such that for all b > 1 we
have
∞
X
α = a +
G (b, i) .
i=0
Let G : N × N → Q be such that, for each b > 1, we have
G (b, i) =
di
b ki
where di ∈ {1, . . . , b − 1} and ki ∈ N and 0 < ki < ki+1 (for all
i ∈ N).
We say that G is a general sum approximation from above of the
real number α if there exists a ∈ Z such that for all b > 1 we have
α = a −
∞
X
i=0
G (b, i) .
Example
π = 3.14159265358979323846264 . . .
Example
π = 3.14159265358979323846264 . . .
Let Ĝ be the sum approximation of π from below.
Example
π = 3.14159265358979323846264 . . .
Let Ĝ be the sum approximation of π from below. Then, we have
π = 3
= 3
+ Ĝ (10, 0)
1
+ 1
10
+ Ĝ (10, 1)
4
+ 2
10
+ Ĝ (10, 2)
1
+ 3
10
+ ...
+ ...
Example
π = 3.14159265358979323846264 . . .
Let Ĝ be the sum approximation of π from below. Then, we have
π = 3
= 3
+ Ĝ (10, 0)
1
+ 1
10
+ Ĝ (10, 1)
4
+ 2
10
+ Ĝ (10, 2)
1
+ 3
10
Let Ǧ be the sum approximation of π from above.
+ ...
+ ...
Example
π = 3.14159265358979323846264 . . .
Let Ĝ be the sum approximation of π from below. Then, we have
π = 3
= 3
+ Ĝ (10, 0)
1
+ 1
10
+ Ĝ (10, 1)
4
+ 2
10
+ Ĝ (10, 2)
1
+ 3
10
+ ...
+ ...
Let Ǧ be the sum approximation of π from above. Then, we have
π = 4
= 4
− Ǧ (10, 0)
8
− 1
10
− Ǧ (10, 1)
5
− 2
10
− Ǧ (10, 2)
8
− 3
10
− ...
− ...
Then, Sg ↑ denotes the set of irrationals that have a general sum
approximation from below in the subrecursive class S.
Then, Sg ↓ denotes the set of irrationals that have a general sum
approximation from above in the subrecursive class S.
Then, Sg ↑ denotes the set of irrationals that have a general sum
approximation from below in the subrecursive class S.
Then, Sg ↓ denotes the set of irrationals that have a general sum
approximation from above in the subrecursive class S.
For any S (closed under elementary operations) and any base b,
we obviously have It is obvious that we have
Sg ↓ ⊆ Sb↓
and
Sg ↑ ⊆ Sb↑ .
Then, Sg ↑ denotes the set of irrationals that have a general sum
approximation from below in the subrecursive class S.
Then, Sg ↓ denotes the set of irrationals that have a general sum
approximation from above in the subrecursive class S.
For any S (closed under elementary operations) and any base b,
we obviously have It is obvious that we have
Sg ↓ ⊆ Sb↓
and
Sg ↑ ⊆ Sb↑ .
and
Sg ↑ ⊂ Sb↑
Moreover, we have
Sg ↓ ⊂ Sb↓
since e.g. S2↓ and S3↓ are incomparable.
Furthermore, it is not very hard to prove that we have
Sg ↓ ⊆ SD
and
Sg ↑ ⊆ SD
for any S closed under elementary operations.
Furthermore, it is not very hard to prove that we have
Sg ↓ ⊆ SD
and
Sg ↑ ⊆ SD
for any S closed under elementary operations.
But I had to work hard to prove that for any S closed under
primitive recursion, we have
Sg ↓ ∩ Sg ↑
=
S[ ]
where S[ ] is the set of irrational numbers that have a continues
fraction in S.
I expect that Sg ↓ 6= Sg ↑ but I have no proof (yet).
I expect that Sg ↓ 6= Sg ↑ but I have no proof (yet).
The next Venn diagram gives a summary.
VENN DIAGRAM II
There is a lot of open problem present. The following one seems
particularly challenging:
There is a lot of open problem present. The following one seems
particularly challenging:
Does the equality
∞
\
b=2
hold?
Sb↑ = Sg ↑
There is a lot of open problem present. The following one seems
particularly challenging:
Does the equality
∞
\
Sb↑ = Sg ↑
b=2
hold?
Does it hold when S is closed under primitive recursion?
Does it hold when S is closed elementary operations, but not
under primitive recursion?
The corresponding equality for base-b expansions does not hold.
This was proved by Lehman, Fundamenta Mathematica 1961
(Mostowski asks if the equality holds in Fundamenta Mathematica
1957).
Lehman applies a result from analytic number theory in his proof.
Some relevant papers:
L. Kristiansen: On Subrecursive Representability of Irrational
Numbers, Computability (the journal of CiE, preprint available
from my homepage).
E. Specker: Nicht Konstruktiv Beweisbare Satze Der Analysis,
The Journal of Symbolic Logic 14(3) (1949), 145–158.
A. Mostowski: On Computable Sequences, Fundamenta
Mathematica 44 (1957), 37–51.
R. S. Lehman: On Primitive Recursive Real Numbers,
Fundamenta Mathematica 49 (1961), 105–118.
K. Ko: On the definitions of some complexity classes of real
numbers, Mathematical Systems Theory 16 (1983), 95–109
Goodbye!
Thanks for your attention!