Download Suppose we have zoomed in on a particular x value or a function

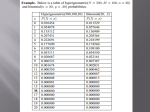
Constructing a linear approximation:
Suppose we have zoomed in on a particular x value or a function, say, x = 3. Then
f (3) 
f (3  h)  f (3)
h
Let’s now use a little bit of algebra to rearrange this to solve for f (3  h) .
f (3  h)  f (3)  f (3)h
We let 3 + h = x, where x is close in value to 3, since h is small. So far so good?
Then h = x – 3. We now make those substitutions.
f ( x)  f (3)  f (3)( x  3)
This is now in the form of a linear equation: y = f(x), the slope m is f (3) , and the
constant is “b”.
This equation is a linear approximation to the graph near x = 3.
Let’s see how this works for the function y  x2 . Suppose we want to approximate the
equation of the parabola with a straight line near x = 3.
We know from our prior work in the previous section that an expression for the
derivative is
f ( x)  2x
So a linear approximation near x = 3 would be:
f ( x)  f (3)  f (3)( x  3)
f ( x)  9  6( x  3)
y  6x  9
The line y = 6x – 9 and the parabola y  x2 are extremely close to each other around
x = 3. We graph both equations to verify this: