Survey
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Abstract: The main problem of approximation theory is to resolve a
Document related concepts
Renormalization group wikipedia , lookup
Scalar field theory wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Inverse problem wikipedia , lookup
Theoretical computer science wikipedia , lookup
Computational chemistry wikipedia , lookup
Strähle construction wikipedia , lookup
Multiple-criteria decision analysis wikipedia , lookup
Reinforcement learning wikipedia , lookup
Linear algebra wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Least squares wikipedia , lookup
Generalized linear model wikipedia , lookup
Transcript
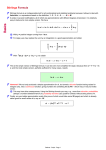
Abstract: The main problem of approximation theory is to resolve a complicated target function by a sequence of functions of small complexity. In linear approximation, the approximating functions are chosen from pre-specified finite-dimensional vector spaces. However, in many problems one can gain considerably by allowing the approximation method to "adapt" to the target function. The approximants will then typically belong to nonlinear manifolds rather than linear spaces, hence the name nonlinear methods of approximation. Nowadays, such methods are used throughout mathematics and science. My goal is to present some basic facts from nonlinear approximation theory in an informal way. In particular, function spaces will be kept to an appropriate minimum. If time permits, I will discuss recent joint work with P. Petrushev (USC) on highly nonlinear spline approximation.
