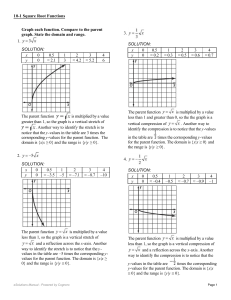
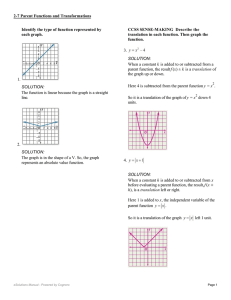
MATH10040 Chapter 3: Congruences and the Chinese Remainder
... Solution: Note that numbers of the form 3y + 2 are precisely the numbers which are congruent to 2 modulo 3. Thus we are required to show that the congruence x2 ≡ 2 (mod 3) has no solutions. Now x leaves either remainder 0, 1 or 2 on division by 3. So x ≡ 0, 1 or 2 (mod 3). We consider each of these ...
... Solution: Note that numbers of the form 3y + 2 are precisely the numbers which are congruent to 2 modulo 3. Thus we are required to show that the congruence x2 ≡ 2 (mod 3) has no solutions. Now x leaves either remainder 0, 1 or 2 on division by 3. So x ≡ 0, 1 or 2 (mod 3). We consider each of these ...
Folding and unfolding in periodic difference equations
... suppose that we have a 6-periodic system [f0 , f1 , . . . , f5 ]. We can define the map F := f5 ◦ f4 ◦ . . . ◦ f0 , then deal with the autonomous equation xn+1 = F (xn ). Define the maps F0 := f1 ◦ f0 , F1 := f3 ◦ f2 , F2 := f5 ◦ f4 , then deal with the periodic alternating system [F0 , F1 , F2 ]. O ...
... suppose that we have a 6-periodic system [f0 , f1 , . . . , f5 ]. We can define the map F := f5 ◦ f4 ◦ . . . ◦ f0 , then deal with the autonomous equation xn+1 = F (xn ). Define the maps F0 := f1 ◦ f0 , F1 := f3 ◦ f2 , F2 := f5 ◦ f4 , then deal with the periodic alternating system [F0 , F1 , F2 ]. O ...
Varieties of cost functions
... n, height at most 3|M | and root in I. Such an equivalence class of functions is called a regular cost function. We keep the reversal order notation as it was introduced in [9]. Example 3. Consider the stabilisation monoid S1 defined in Example 2 and let I = {0}. Let h : {a, b} → M be the labelling ...
... n, height at most 3|M | and root in I. Such an equivalence class of functions is called a regular cost function. We keep the reversal order notation as it was introduced in [9]. Example 3. Consider the stabilisation monoid S1 defined in Example 2 and let I = {0}. Let h : {a, b} → M be the labelling ...
A Common Recursion For Laplacians of Matroids and Shifted
... shifted simplicial pair (Theorem 5.7). This naturally generalizes a formula for a single shifted complex [16]; the graph case goes back to Merris [29]. Similarly, we generalize a related conjectured inequality on the Laplacian spectrum of an arbitrary simplicial complex [16] to an arbitrary simplici ...
... shifted simplicial pair (Theorem 5.7). This naturally generalizes a formula for a single shifted complex [16]; the graph case goes back to Merris [29]. Similarly, we generalize a related conjectured inequality on the Laplacian spectrum of an arbitrary simplicial complex [16] to an arbitrary simplici ...
Linear Algebra Course Notes 1. Matrix and Determinants 2 1.1
... (3) Existence of 0 There exists an element 0, such that for any elemnt a ∈ F ,a + 0 = a. (4) Existence of opposite For any element a ∈ F , There exists an element called −a, such that a + (−a) = 0 (5) Commutativity of × For any two elements a, b ∈ F , we have a × b = b × a (6) Associativity of × For ...
... (3) Existence of 0 There exists an element 0, such that for any elemnt a ∈ F ,a + 0 = a. (4) Existence of opposite For any element a ∈ F , There exists an element called −a, such that a + (−a) = 0 (5) Commutativity of × For any two elements a, b ∈ F , we have a × b = b × a (6) Associativity of × For ...
Maple reference sheet (goes with lab 1)
... Expands the expression using the well-known trig identity for sine of a sum. expand(exp(2*x)); Expands e2x to the product ex ex. simplify(expr); Algebraically simplifies expr. subs(x=a,expr); Substitutes a for x at each occurrence of x in expr. The value of a could be a number or an algebraic ...
... Expands the expression using the well-known trig identity for sine of a sum. expand(exp(2*x)); Expands e2x to the product ex ex. simplify(expr); Algebraically simplifies expr. subs(x=a,expr); Substitutes a for x at each occurrence of x in expr. The value of a could be a number or an algebraic ...
Accessible Accuplacer Elementary Algebra Study Guide for Screen
... The following sample questions are similar to the format and content of questions on the Accuplacer Elementary Algebra test. Reviewing these samples will give you a good idea of how the test works and just what mathematical topics you may wish to review before taking the test itself. Our purposes in ...
... The following sample questions are similar to the format and content of questions on the Accuplacer Elementary Algebra test. Reviewing these samples will give you a good idea of how the test works and just what mathematical topics you may wish to review before taking the test itself. Our purposes in ...
Equation

In mathematics, an equation is an equality containing one or more variables. Solving the equation consists of determining which values of the variables make the equality true. In this situation, variables are also known as unknowns and the values which satisfy the equality are known as solutions. An equation differs from an identity in that an equation is not necessarily true for all possible values of the variable.There are many types of equations, and they are found in all areas of mathematics; the techniques used to examine them differ according to their type.Algebra studies two main families of equations: polynomial equations and, among them, linear equations. Polynomial equations have the form P(X) = 0, where P is a polynomial. Linear equations have the form a(x) + b = 0, where a is a linear function and b is a vector. To solve them, one uses algorithmic or geometric techniques, coming from linear algebra or mathematical analysis. Changing the domain of a function can change the problem considerably. Algebra also studies Diophantine equations where the coefficients and solutions are integers. The techniques used are different and come from number theory. These equations are difficult in general; one often searches just to find the existence or absence of a solution, and, if they exist, to count the number of solutions.Geometry uses equations to describe geometric figures. The objective is now different, as equations are used to describe geometric properties. In this context, there are two large families of equations, Cartesian equations and parametric equations.Differential equations are equations involving one or more functions and their derivatives. They are solved by finding an expression for the function that does not involve derivatives. Differential equations are used to model real-life processes in areas such as physics, chemistry, biology, and economics.The ""="" symbol was invented by Robert Recorde (1510–1558), who considered that nothing could be more equal than parallel straight lines with the same length.