* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download experimentfest 2015 - University of Newcastle
Elementary particle wikipedia , lookup
Electromagnet wikipedia , lookup
Circular dichroism wikipedia , lookup
Classical mechanics wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Anti-gravity wikipedia , lookup
Nuclear physics wikipedia , lookup
Lorentz force wikipedia , lookup
Speed of gravity wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
History of physics wikipedia , lookup
High-temperature superconductivity wikipedia , lookup
History of subatomic physics wikipedia , lookup
Electromagnetism wikipedia , lookup
Thomas Young (scientist) wikipedia , lookup
Faster-than-light wikipedia , lookup
Condensed matter physics wikipedia , lookup
Wave–particle duality wikipedia , lookup
Photoelectric effect wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Chien-Shiung Wu wikipedia , lookup
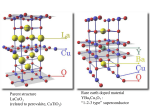
EXPERIMENTFEST 2015 HANDBOOK Physics CONTENTS Introduction 3 Welcome 4 Studying Physics 6 Charged Particles in Electric and Magnetic Fields 8 Michelson-Morley Experiment 11 Wilson Cloud Chamber 14 The Photoelectric Effect 15 Reference Frames 19 Superconductivity 20 Projectile Motion - Uniformly Accelerated Motion in Two Spatial Dimensions 23 Experiment Fest Page 2 INTRODUCTION ExperimentFest is an experiment program designed to provide enriching educational experiences for senior high school students who are studying Physics, Chemistry and Biology. ExperimentFest is supported by the University of Newcastle’s Faculty of Science and Information Technology and takes place at both the Callaghan and Ourimbah (Central Coast) campuses of the University of Newcastle. Callaghan Campus: Physics - Friday 12 – Thursday 18 June, 2015 Chemistry - Monday 15 – Friday 19 June, 2015 Biology - Friday 12 - Friday 19 June, 2015 Ourimbah Campus: Biology, Physics & Chemistry Monday 22 - Thursday 25 June, 2015 Tuncurry: Physics - Saturday 20 June, 2015 All experiments are complemented by notes, follow-up discussions and questions to enhance your learning experience. For booking information contact: Larry Milton on 0404 460 470; or David Rushton on 4333 6965 or 0414 238 464 Experiment Fest Page 3 WELCOME Welcome to the Faculty of Science and Information Technology at the University of Newcastle. ExperimentFest is a wonderful chance to give you practical experience which complements your classroom learning while giving you a first hand look at University life and facilities. Science is an exciting field of study, allowing you to move with the times and contribute actively and responsibly to society. There are many education opportunities in science after high school. Here in the Faculty we provide study and research programs in fastmoving modern fields that make our world work. The Faculty staff and students who will be taking you through the experiments today are involved in contemporary science research. Please ask questions and utilise your time with them. Take this day to enjoy being out of the class room, exploring science with fellow students and participating in valuable experiments and discussions which will help you in your HSC and beyond. I wish you well in your studies. I hope you apply yourselves to the learning process with enthusiasm and you enjoy your time at the University. We hope to see you studying with us in the future! Best wishes, Prof. Eileen McLaughlin Pro Vice-Chancellor – Faculty of Science and Information Technology University of Newcastle Experiment Fest Page 4 PHYSICS Experiment Fest Page 5 STUDYING PHYSICS Why study physics? Physics is crucial to understanding the world around us, the world inside us, and the world beyond us. It is the most basic and fundamental science. Physics challenges our imaginations with concepts like relativity and string theory, and it leads to great discoveries, like computers and lasers, that change our lives. Physics encompasses the study of the universe from the largest galaxies to the smallest subatomic particles. Moreover, it’s the basis of many other sciences, including chemistry, oceanography, seismology, and astronomy. All are easily accessible with a bachelor’s degree in physics. The importance of physics isn’t limited to the “hard sciences.” Increasingly, physicists are turning their talents to molecular biology, biochemistry, and biology itself. Even medicine has a niche for physicists, and since medical physicists are hard to come by, they are much in demand. Physics also supports many new technologies. Cell phones, the Internet, and MRIs are only a few examples of the physics-based technological developments that have revolutionized our world. A physics education equips a person to work in many different and interesting places in industrial and government labs, on college campuses, and in the astronaut corps. Many theoretical and experimental physicists work as engineers, and many engineers have physics degrees. In addition, many physics grads leave the lab behind and work at newspapers and magazines, in governmental departments—places where their problem-solving abilities and analytical skills are great assets. Physics is interesting, relevant, and it can prepare you for great jobs in a wide variety of places. Opportunities for further studies in Physics: The Bachelor of Science degree program at the University of Newcastle provides a foundation of knowledge, skills and attributes that allows graduates to be employable not just today but into the future and to contribute actively and responsibly to society. Majoring in Physics, you have the opportunity to sample and/or specialise in any one of the following: • • • • • • • • • • • Biophysics (double major) Computational Physics (double major) Geophysics (double major) Medical Physics Nanotechnology Optical Physics (double major) Research Physics Space Physics/Radar/Surveillance Majoring in Photonics you can study: Optical Physics (double major) Optical Physics/Laser Engineering/Photonics Engineering Experiment Fest Page 6 Research in Physics at the University of Newcastle: There are various groups here at the University which are committed to research in physics. Groups include: • Centre for Space Physics • Medical Physics Group • Surface and Nanoscience Group • Research Centre for Organic Electronics Careers in Physics: The Faculty of Science and IT care about our students and are interested in giving as much direction as possible to those making career choices and beyond. The possible career paths listed below include a range of opportunities for graduates at degree, honours, and post graduate study levels. • • • • • • • • • • • • Acoustical Physicist Astronomer/ Astrophysicist Biophysicist Cosmologist Fluid Dynamics Analyst Geophysicist Graduate Trainee (Graduate Program) Health Physicist Laboratory Analyst Laboratory/Research Assistant Nanotechnologist Nuclear Physicist • • • • • • • • • • • • Optical Physicist Plasma Physicist Research Scientist Risk Analyst Science Information/ Education Officer Science/ Physics Teacher Science Technician Scientific Patent Attorney/ Technical Advisor Scientific Policy Officer Scientific Writer Software Engineer/ Tester University Lecturer/ Academic Possible careers in Photonics: • • • • • • • • • • Graduate Trainee (Graduate Programs) Laser Engineer Manufacturing Engineer Nanotechnologist Network Cabling Technician Network Support Engineer Optical Research Scientist Photonics Engineer Project Manager Research Scientist • • • • • • • • • • Sciences Technician Scientific Patent Attorney Scientific Policy Officer Scientific Writer Systems Engineer Technical Sales Representative Technology Infrastructure Manager Telecommunications Service Delivery Test Engineer University Lecturer/Academic For more information please visit the University’s website: www.newcastle.edu.au For more information on the Faculty of Science and IT check out our website: www.newcastle.edu.au/science-it Experiment Fest Page 7 CHARGED PARTICLES IN ELECTRIC AND MAGNETIC FIELDS Extract from HSC Syllabus 9.4.1 describe quantitatively the force acting on a charge moving through a magnetic field; F=qvBsinθ Solve problems and analyse information using F=qvBsinθ, F=qE, E=V/d. Outline Thomson’s experiment to measure the charge/mass ratio of an electron Key Words • • • • • • • Magnetic and electric fields Helmholtz coils Electron gun Deflection plates Circular Motion Electric charge Introduction During the 1800s it was believed that the atom (Greek word meaning indivisible) was the fundamental particle of all matter. In the mid 1800s W. Crookes (UK, 1832-1919) invented the equipment that allowed scientists to investigate ‘cathode rays’. The Crookes tube or discharge tube consists of a glass tube containing a pair of separated metal plates or electrodes. The electrodes were named the anode and the cathode. The experiments involved applying a large voltage to the plates and investigating the properties of the ‘rays’ in the tube as a function of gas pressure etc. What are Cathode rays? This question was investigated by J.J Thomson (UK, 1856-1940) in 1897. There are 3 famous physicists named ‘Thomson’. 1. William Thomson (1824-1907); Also known as Lord Kelvin, known for the absolute temperature scale. 2. Joseph J. Thomson (1856-1940); our guy, discovery of the electron, proposed a ‘plum pudding’ atomic model 3. George P. Thomson (1892-1975); Son of J.J Thomson, diffraction of electrons to prove wave nature Using the observed effects of electric and magnetic fields on the cathode rays, J.J. Thomson estimated the charge/ mass ratio. From the results of Faraday’s (UK, 1791-1867) Law of Electrolysis, Thomson was able to estimate that cathode rays consisted of negatively charged particles that were about 1800 times lighter than hydrogen. Robert Millikan more precisely measured the electron charge in 1909. Experiment Fest Page 8 Effect of the Electric Field A voltage is applied across the deflection plates in the tube. If the electric field is assumed to be uniform, then the expression for the electric field, E is E= and the electrons experience a force given by F= The electron beam is made visible by collisions of gas atoms in the tube and with the mica screen. a) Draw a diagram showing the expected path of an electron after it enters the electric field. v electron gun b) How can you tell if the charge on the particles is +ve or -ve? Assume an electron travels with an initial velocity, v0 in the horizontal (x) direction and encounters a uniform electric field in the y direction. c) In which direction is the force on the electron? d) What is the shape of the curve traced out by the path of the electron? Experiment Fest Page 9 Effect of the Magnetic Field The magnetic field is generated by a Helmholtz coil arrangement e) In what direction is the magnetic field when it intersects the electron beam? In the magnetic field, the electrons experience a force given by F= f) In what direction is this magnetic force? g) What is the shape of the curve traced out by the electron due to the force caused by the magnetic field? This means that the magnetic force (Bqv sinθ) acts as a centripetal force: so, Bqv sinθ = mv2 , and if θ is 900 then Bqv = mv2 r r Fc = mv2 r By rearranging the above equation the charge/mass ratio: q/m = (Equation 1) The radius of curvature, r is given by r = (x2 + y2) / (2y). This can be measured from the grid scale on the tube. The value of r is = ............................ Charge to Mass Ratio 1. Ensure the current in the Helmholtz coils is zero (no magnetic field). 2. Switch on the electric field. 3. Increase the current to the Helmholtz coils until the cathode ray beam flattens out. At this point the forces from the two fields, acting on the cathode ray beam, are equal. ie, Felectric field = Fmagnetic field or,Eq = Bqv simplifying this will give E = Bv and rearranging for v: v=E B Adjust the current to the coils until the trace intersects the coordinate (10,0) on the grid. Use the value of the current, I, to calculate the magnetic field, B, by: B=0.00423 I h) Calculate the value of B from the given value of I. i) Estimate the deflection plate separation from the grid scale. This is the value for d. d = ...................m. The potential difference between the charged plates, V, has a value of ...........................V j) Calculate the value of the electric field E using: E = V E = ............................Vm-1 d k) Combine equations 1 and 2 by substituting for v in equation 1 and find the charge/mass ratio, q/m for a cathode ray particle. q/m = l) What is the accepted value for q/m ? Experiment Fest Page 10 MICHELSON-MORLEY EXPERIMENT HSC Syllabus 9.2.4 Describe and evaluate the Michelson-Morley attempt to measure the relative velocity of the Earth through the aether Gather and process information to interpret the results of the Michelson-Morley experiment What is the nature of Light? Around 1800 it was thought that light was a wave because it produced interference and diffraction patterns. Michelson’s (in 1879) calculated the speed of light, using an arc lamp and rotating mirrors, to be 186,350 miles per second (299,901 kilometres per hour). Like waves travelling through water it was thought that light must be similarly travelling in some mysterious material, which was called the aether, surrounding and permeating everything even space. Since light travels so fast, the aether must be very light and very hard to compress. It must also allow solid bodies to pass through it freely, without ether resistance, or the planets would be slowing down. How could the Aether be detected? Michelson explained the puzzle to his children as follows: Suppose we have a river of width w (say, 100 units), and two swimmers who both swim at the same speed, (say, 5 units per second). The river is flowing at a steady rate, say 3 units per second. The swimmers race in the following way: they both start at the same point on one bank. One (Joe) swims directly across the river to the closest point on the opposite bank, then turns around and swims back. The other (Bob) stays on one side of the river, swimming upstream a distance (measured along the bank) exactly equal to the width of the river, then swims back to the start. Who wins? Let’s consider Bob who goes upstream and back. Going 100 units upstream, the speed relative to the bank is only 2 units per second, so that takes 50 seconds. Coming back, the speed is 8 feet per second, so it takes 12.5 seconds, for a total time of 62.5 seconds. Now Joe goes across the flow which is little trickier. To succeed in going directly across, Joe must actually aim upstream at the correct angle. If the angle is correctly chosen so that the net movement is directly across, in one second Joe must have moved four units across (see diagram). So, at a crossing rate of 4 units per second, Joe gets across in 25 seconds, and back in the same time, for a total time of 50 seconds so Joe wins. This turns out to true whatever their swimming speed. (Of course, the race is only possible if they can A swim faster than the current!) Experiment Fest Page 11 Michelson thought that just as the speed of sound is relative to the air, so the speed of light must be relative to the ether. So if you could measure the speed of light then you could measure the speed of light travelling upwind, and compare it with the speed of light travelling downwind, and the difference of the two measurements should be twice the windspeed. The Experiment Light is directed at an angle of 45 degrees at a half-silvered, half transparent mirror, so that half the light goes on through the glass, half is reflected. They both go on to distant mirrors which reflect back to the half-silvered mirror. At this point, the light is again half reflected and half transmitted, but a telescope is placed behind the half-silvered mirror as shown in the figure so that the combined light will arrive in this telescope. Now, if there is an ether wind blowing, someone looking through the telescope should see the effect of a slightly longer time for the 2 light beams to arrive, since one would have gone more upstream and back, one more across stream in general. Taking the speed of light to be c relative to the aether, and the ether to be flowing at v: to go a distance l upstream will take l/(c-v) seconds and l downstream will take l/(c+v) seconds, therefore the total roundtrip takes 2 l / (c (1- v2/c2)) seconds. We can safely assume the speed of the aether is much less than the speed of light, otherwise it would have been noticed long ago, for example in timing of eclipses of Jupiter’s satellites. This means v2/c2 is a small number so we approximate the roundtrip time to go upstream and downstream to be (2 l / c)(1+v2/c2). From Pythagoras’ theorem, the cross-stream speed is √ (c2-v2). The roundtrip crossstream time will be 2l / √ (c2-v2). This can be approximated as (2l/c)(1+v2/2c2). The two roundtrip times differ by an amount (l)(v2/c3). Now, 2l/c is just the time the light would take if there were no aether wind at all, say, a few millionths of a second. If we take the ether windspeed to be equal to the earth’s speed in orbit, then v2/c2 is about 1/100,000,000. This means the time delay between the pulses reflected from the different mirrors reaching the telescope is about one-hundred-millionth of a few millionths of a second. It seems completely hopeless that such a short time delay could be detected. Experiment Fest Page 12 Michelson was the first to figure out how to do it using the interference properties of the lightwaves. One set of waves goes upstream and downstream, the other goes across stream and back. Finally, they come together into the telescope and the eye. If the one that took longer is half a wavelength behind, its troughs will be on top of the crests of the first wave, they will cancel, and nothing will be seen. If the delay is less than that, there will still be some dimming. However, slight errors in the placement of the mirrors would have the same effect. To maximize the effect, the whole apparatus, including the distant mirrors, was placed on a large turntable so it could be swung around. Observe how the interference pattern changes as the turntable is rotated through 90 degrees. What happens? How does this change compare to that expected if there is an aether? Why was the null result difficult to accept? Experiment Fest Page 13 WILSON CLOUD CHAMBER Extract from HSC Syllabus 9.8.3 Perform a first-hand investigation or gather secondary information to observe radiation emitted from a nucleus using Wilson Cloud Chamber or similar detection device The cloud chamber, also known as the Wilson chamber, is used for detecting particles of ionising radiation. In its most basic form, a cloud chamber is a sealed environment containing a supercooled, supersaturated alcohol vapour. When an alpha particle or beta particle interacts with the mixture, it ionizes it. The resulting ions act as condensation nuclei, around which a mist will form (because the mixture is on the point of condensation). The high energies of alpha and beta particles mean that a trail is left, due to many ions being produced along the path of the charged particle. These tracks have distinctive shapes (for example, an alpha particle’s track is broad and straight, while an electron’s is thinner and shows more evidence of deflection by collisions). When any uniform magnetic field is applied across the cloud chamber, positively and negatively charged particles will curve in opposite directions, according to the Lorentz force law with two particles of opposite charge (http://en.wikipedia.org/wiki/Cloud_chamber) In this demonstration we will use a Diffusion Cloud Chamber 600 (Andrews University, MI, USA) to observe ionizing radiation from cosmic rays and also from a Pb210 source. Pb210 has two decay paths. (i) It decays to Hg206 by emission of a 3.72MeV alpha particle. Hg206 then decays to Tl206 by beta particle emission. (ii) Pb210 also decays to Bi210 by beta particle emission. In both decay paths gamma rays are also emitted. Observe the tracks from the Pb210 source. Can alpha particle and beta particle tracks be identified? Observe tracks when the source is removed. Where do those tracks come from? Observe what happens to the tracks when a magnet is placed in the cloud chamber. Experiment Fest Page 14 THE PHOTOELECTRIC EFFECT Extract from HSC Syllabus: 9.4.2 Explain the particle model of light in terms of photons with particular energy and frequency. Solve problems, analyse information and identify the relationship between photon energy, frequency, speed of light and wavelength. When light shines on a metal surface electrons are ejected if the frequency (energy) of the light is above the Threshold Frequncy (Work Function) of the metal. The energy carried away by each electron depends on the frequency but not on the intensity of light. Therefore, light can be considered to be a stream of particles (photons) rather than a wave. The emitted electrons have a range of kinetic energies. The electrons with maximum kinetic energy are emitted from right at the surface after having received all the energy, E, from the photon. However, in leaving the surface the electrons lose an amount of energy φ (called the workfunction of the surface). Read the above section and write down an expression for the maximum kinetic energy of the electrons in terms of the photon energy E and workfunction φ. Max kinetic energy = (1) The energy of a photon is given by E = hf, where Planck’s constant h is 6.63 x 10-34 Js and f is the frequency of the photon in Hz and c = fλ where the speed of light c is 3.00 x108 ms-1 and the wavelength of the photon is λ. Write down an expression for E in terms of λ. E = (2) Combine (1) and (2) to write down a relation between maximum kinetic energy and λ Maximum kinetic energy = (3) Experiment Fest Page 15 The Experiment To determine maximum kinetic energy of emitted electrons. The phototube (Fig 2) is the essential part of the instrument you will use. It is an evacuated glass tube containing a coated electrode (cathode) shaped like half of a cylinder. Another electrode (anode) in the form of a straight rod is positioned at approximately the focal point of the curved surface. When light strikes the cathode surface, electrons are ejected and collected by the anode. The coloured filters, placed into the light path, cut off all wavelengths above a particular value, therefore the minimum wavelength of light reaching the tube is known. Eqn 3 can then be used to determine the maximum kinetic energy of the emitted electrons. To measure the highest electron energy we apply a small reverse voltage called the “backing voltage” (ie with anode negative and cathode positive) that is just high enough to completely stop the flow of electrons reaching the anode (absolutely zero current). Note: If the backing voltage is continued to be increased, the current will begin to flow backwards because electrons begin to flow from the anode to the cathode. The Experimental Method 1. Have the demonstrator check the equipment. Turn on the light source light source to illuminate the phototube through the aperture in the rear face of the instrument. Note that the light source will become warm. 2. Insert one of the filters into the wider pair of the slide grooves provided in front of the light source. 3. Select tube current on the meter switch to monitor the current through the phototube. Select the 0-20μA range. 4. Using the backing voltage control, adjust the voltage from zero volts until the current through the tube reduces below 0.1 microamp. 5. Now select the sensitive 0-200nA range and increase the backing volts until the electron flow through the tube is reduced to 0.0 nanoamps. If the current goes negative reduce the backing volts until 0.0 nanoamps is achieved. At this point the most energetic electrons are prevented from reaching the anode. Experiment Fest Page 16 Fig 3 6. Without disturbing anything, select backing volts on the meter switch and observe the exact voltage that is being applied to the phototube in reverse to stop all electrons from reaching the anode. Record this backing voltage in table1. 7. Remove the colour filter and repeat the experiment from steps 3 to 7 for the remaining colour filters. 8. Using the wavelength value marked on the blue filter, calculate the frequency (in Hertz) of the light transmitted by this filter and enter it into table 1. Record your measurements of backing voltage in table 1. 9. Plot a graph of the frequency in Hz (X axis) against the backing volts in Volts (Y axis) using the supplied graph paper. Table 1 Frequency f = c/ λ (Hz) Filter Wavelength (nm) blue 450 yellow 480 6.25 x 1014 orange 545 5.50 x 1014 red 590 5.08 x 1014 Backing Volts (V) Discussion The stopping voltage is related to the maximum kinetic energy of the electrons since if the electrons have more energy it will require a larger voltage to stop them. So which colour light generates electrons with the highest kinetic energy? Which colour light generates electrons with the lowest kinetic energy? Is this expected from equation 3? What can we say about the slope of the line in this graph? Experiment Fest Page 17 The intercept on the Y axis is related to the workfunction of the cathode. Using eqn 1, determine the workfunction of the cathode in eV. What is the metal cathode surface most likely made from? Use the list workfunctions on the graph paper to determine your answer. Extension With the red filter selected, place an aperture in the light path to reduce the intensity of light. Does this markedly change the backing volts? Is this result expected? Experiment Fest Page 18 REFERENCE FRAMES Extract from HSC Syllabus 9.2.4 Students perform an investigation to help distinguish between inertial and noninertial frames of reference. A reference frame which moves at constant velocity with respect to another is called an inertial reference frame. Forces act the same way in this frame as in the original frame. In the experiment below, a cart carrying a pendulum sits on an inclined plane. In the frame of the cart the pendulum hangs directly down, if the cart is stationary. Predict how the pendulum hangs if the cart is moving down the track at constant velocity. Is this what happens experimentally? If the cart is moving at constant velocity we have an inertial frame of reference. The behaviour of inertial frames was described in Einstein’s special theory of relativity. But what happens if the frame is accelerating i.e. if we have a non-inertial frame of reference? So how should the pendulum hang if the cart is accelerating down the track? Should it (i) hang straight down (ii) hang perpendicular to the incline or (iii) in some other direction? Is this what happens experimentally? We can explain this behaviour by saying that (i) Newton’s laws don’t work in an accelerating frame of reference or (ii) that we need extra “fictitious” forces to make Newton’s laws work. Newton’s principle of equivalence says that physics can be explained in accelerating frames by the use of gravitational forces. In what direction should gravity point in the cart’s frame of reference to explain the position of the pendulum? Experiment Fest Page 19 SUPERCONDUCTIVITY Extract from HSC Syllabus 9.4.4 Process information to identify some of the metals, metal alloys and compounds that have been identified as exhibiting the property of superconductivity and their critical temperatures. Process information to discuss possible applications of superconductivity and the effects of those applications on computers, generators and motors and transmission of electricity through power grids. Discuss the advantages of using superconductors and identify limitations to their use Gather and process information to describe how superconductors and the effects of magnetic fields have been applied to develop a maglev train. Process information to discuss possible applications of superconductivity and the effects of those applications on computers, generators and motors and transmission of electricity through power grids. Early in the 20th century, Dutch physicist Heike Kamerlingh Onnes observed that mercury displayed no electrical resistance when cooled to very low temperatures. Superconductivity became a scientific curiosity with few practical applications. Then in the 1960s a practical superconducting metal wire made of niobium and tin was developed. The niobium and titanium alloy, still in use today, is among the materials called low-temperature superconductors. Low-temperature superconductors must be cooled to below 20 Kelvin (-253o Celsius) in order to become superconducting. They are now widely used in magnetic resonance imaging, or MRI, machines, and in the fields of high-energy physics and nuclear fusion. Additional commercial use has been limited largely by the high refrigeration costs associated with liquid helium, which is needed to cool the materials to such low temperatures. The hope for low-cost superconductivity was ignited by two significant discoveries in the 1980s. In 1986, two IBM scientists in Zurich, Alex Muller and Georg Bednorz, discovered a new class of superconductors. Unlike the lowtemperature superconductors, which were metallic or semimetallic, these new compounds were ceramic and were superconducting up to 35 K (-238oC). Muller and Bednorz won a Nobel Prize for their discovery. Then in 1987, Paul Chu at the University of Houston took the discovery one step further and announced a compound that became superconducting at 94 K (-179oC). This discovery was particularly significant because this compound could be cooled with cheap and readily available liquid nitrogen. These new materials were called high-temperature superconductors. Bismuth-based compounds are being fashioned into superconducting wires and coils, which are becoming essential to electric power uses. Thallium- and yttriumbased compounds are being formed into the thin films used in electronic devices. Identify metals, alloys and compounds used as superconductors and their critical temperatures. metals, metal alloys and compounds Experiment Fest Page 20 critical temperatures 1. 2. 3. 4. 5. 6. 7. Power transmission cables that carry current without energy losses will increase the capacity of the transmission system, saving money, space, and energy. Prototype power transmission cables have been developed and are being tested by teams led by Pirelli Cable Company and Southwire Company . Motors made with superconducting wire will be smaller and more efficient. A 1,000-horsepower motor has been constructed and is undergoing testing by an SPI team led by Rockwell Automation/Reliance Electric Company. Generators will use superconducting wire in place of iron magnets, making them smaller and lighter. New generators also may get more power from less fuel. An SPI team led by General Electric has developed a design for a 100-megavoltampere generator. Current controllers (i.e., fault-current limiters) help utilities deliver reliable power to their customers. HTS fault-current limiters detect abnormally high current in the utility grid (caused by lightning strikes or downed utility poles, for example). They then reduce the fault current so the system equipment can handle it. An SPI team led by General Atomics recently produced a successful HTS fault-current limiter that will soon be ready to market. Energy storage in flywheel systems will ensure the quality and reliability of the power transmitted to utility customers. In addition, energy storage provides utilities with cost savings by allowing them to store energy when the demand for electricity is low and generating the power is cheap. This stored energy is then dispensed when demand is high and power production is more expensive. Magnetic resonance imaging (MRI) machines enhance medical diagnostics by imaging internal organs—often eliminating the need for invasive surgeries. MRIs, which currently are made with low-temperature superconductors, will be smaller and less expensive when made with HTS. Maglev trains seem to float on air as a result of using superconducting magnets. These trains have been under development in Japan for two decades; the newest prototype may exceed 547 kilometers per hour. Discuss possible applications of superconductors and the effect of those applications as well as advantages or limitations of superconductors. applications of superconductivity effects advantages or limitations Experiment Fest Page 21 Experiment • Perform an investigation to demonstrate magnetic levitation • Analyse information to explain why a magnet is able to hover above a superconducting material that has reached the temperature at which it is superconducting Observe the demonstrator fill the foam container with liquid nitrogen to slightly cover the superconductor and let the liquid nitrogen boil off until the surface is uncovered – the Yttrium Barium Copper Oxide (YBCO) sample will be near 77K and superconducting. Place the magnet on the superconductor and observe that it is levitating. Observe what happens when the nitrogen all boils off and the sample warms up. What happens? Explanation Superconductors exclude magnetic fields, a property called the Meissner effect. This effect causes a small magnet to levitate above the superconductor surface. As the magnet is brought towards the superconductor, current loops are set up in the superconductor which generate magnetic fields to oppose the magnetic field created by the magnet. The field set up by the superconductor will propagate outside the superconductor and cause the magnet to levitate even though the magnet has come to a stop above the superconductor surface. This is because the superconductor has zero resistance and so the currents will continue to flow after the magnet has stopped. The levitating magnet does not slide off the Rare earth magnet superconductor. This is a manifestation of Flux Pinning, a phenomena associated with Type II superconductors, such as high temperature ceramic superconductors. Here lines of magnetic flux associated with a magnet can penetrate the bulk of the superconductor in the form of magnetic flux tubes. These flux tubes are then pinned to imperfections or impurities in the crystalline matrix of the superconductor thereby pinning the magnet. Experiment Fest Page 22 Superconductor YBa2Cu3O7 Induced currents PROJECTILE MOTION UNIFORMLY ACCELERATED MOTION IN TWO SPACIAL DIMENSIONS Extract from HSC Syllabus: 9.2.2 Describe the trajectory of an object undergoing projectile motion within the Earth’s gravitational field. Perform a first hand investigation, gather information and analyse data to calculate the initial and final velocity, maximum height reached, range and time of flight of a projectile for a range of situations by using simulations, dataloggers and computer analysis. In physics we classify different types of motion so that we can predict where things will end up. Usually, study of motion in physics begins by considering distance and speed where Distance = speed x time (1) This will predict a car’s distance travelled provided the car neither speeds up nor slows down, i.e. for a constant speed. Speed is a scalar quantity (it only has a size or magnitude). If we give the speed a direction as well as a magnitude then we make a vector quantity called velocity. Distance is also a scalar quantity while displacement is a vector quantity. If the car accelerates uniformly with acceleration, a, then the distance travelled in a time, t, is Distance = ut + ½ at2 (2) Equation (2) also allows for the case where the car has an initial constant speed, u, and then accelerates. We now have the main ingredients for examining motion on two dimensions. Acceleration and force are related to the mass of the object, i.e. it is more difficult to move a heavy object. Gravity provides a force in the vertical direction and we’ll call the vertical direction, y. Projectile motion is viewed in two dimensions as the combination of two component motions, one in the horizontal, the x direction, and the other in the vertical or the y direction. Equations 1 and 2 are the basis (in physics) of projectile motion. Equation (1) describes motion along the horizontal while the ‘a’ in equation (2) is the acceleration due to gravity. The following table shows the quantities used in the horizontal and vertical components of projectile motion, as vectors or scalars. Vectors Scalars Displacement – ∆x and ∆y Time Initial velocity – ux and uy Final velocity – vx and vy Acceleration – ax and ay Experiment Fest Page 23 The vector components require the use of positive (+) and negative (-) signs to show the direction of travel. Arbitrarily we chose a positive (+) sign for motion in an upward or vertical direction and a minus (-) sign for motion in the downwards or horizontal direction. Using the symbols from the table equations 1 and 2 become: ∆x = uxt (3) ∆y = uyt + ½ ayt2 (4) Typically for projectile motion ay = -g where g=9.8ms-2. Then equations (3) and (4) can be solved to determine the maximum height, H, reached and the maximum horizontal distance, R, travelled before the object returns to its original height. H = uy2 / 2g (5) R = 2uxuy / g (6) In this exercise you will be able to examine a video of projectile motion. The computer software allows you to obtain the x, y coordinates of a softball at various times during the motion. From these data, various physical quantities can be studied as the ball traces out projectile motion. By now, you would have completed a unit on projectile motion at school. Experiment Fest Page 24