* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download E-Halliburton chapter 13
Genetics and archaeogenetics of South Asia wikipedia , lookup
Group selection wikipedia , lookup
Hardy–Weinberg principle wikipedia , lookup
Dual inheritance theory wikipedia , lookup
Pharmacogenomics wikipedia , lookup
History of genetic engineering wikipedia , lookup
Medical genetics wikipedia , lookup
Dominance (genetics) wikipedia , lookup
Genetic engineering wikipedia , lookup
Koinophilia wikipedia , lookup
Public health genomics wikipedia , lookup
Genetic testing wikipedia , lookup
Selective breeding wikipedia , lookup
Polymorphism (biology) wikipedia , lookup
Designer baby wikipedia , lookup
Genetic drift wikipedia , lookup
Genome (book) wikipedia , lookup
Behavioural genetics wikipedia , lookup
Human genetic variation wikipedia , lookup
Microevolution wikipedia , lookup
Population genetics wikipedia , lookup
BI3010H07
Halliburton chapter 13
A quantitative trait shows a continuous range of phenotypes. This is due to
the contribution from many polymorphic loci and their genotypic
combinations, as well as a modifying influence from the environment. A
typical quantitative genetic trait is body height in humans; although there is
clearly a genetic basis for the observed variability, clear-cut, discrete
genotypes cannot be identified in the way we can for qualitative, single-locus
traits.
There are two principal types of quantitative traits;
1. True quantitative traits which shows continuous phenotypic distributions
2. Meristic traits (e.g. vertebra count) which shows discrete phenotypes
(integer values), but which has a quantitative basis.
Closely related to these are the "Threshold traits", where individuals are
classified as either having the trait or not, although the underlying basis is
quantitative. Many of these are classification traits, like e.g. high blood
pressure or obesity. For all three types of quantitative traits, the analytical
methods for analysing them are the same.
1
BI3010H07
Halliburton chapter 13
On the second page of this chapter (p. 526), Halliburton presents a list of six questions
concerning quantitative traits which he sets out to answer underway:
1. What is the genetic basis of quantitative traits; that is, are they subject to the rules of
Mendelian inheritance?
2. How do we separate genetic effects from environmental effects on a quantitative trait?
3. How many loci affect quantitative traits, and how large are their effects?
4. How much genetic variation for quantitative traits is there in natural populations?
5. How is this genetic variation maintained?
6. How important are mutation, linkage, dominance, epistasis, and pleiotrophy in the
evolution of quantitative traits?
During his treatment of various topics in this chapter, Halliburton remains true to this task.
You will notice in many places that he presents the stuff in such a way as to show the
connection between qualitative and quantitative genetics (for example, by showing how
population means are tied to allele- and genotype frequencies).
2
BI3010H07
Halliburton chapter 13
It is commonly observed that tall parents tend to have tall children and vice versa.
Actually, the expectation is that the offspring performs intermediate between the
parents for additive, quantitative traits.
So, how many polymorphic loci are behind a quantitative trait? The answer is
usually that the number is not known, but probably high. On the other hand a
relatively small set of loci (<10) can create a quite smooth, continuous distribution
of phenotypes (cf Fig. 13.2 with explanation p.530-531). An important notice is
that the contribution from each locus needs not, and probably rearly does,
contribute equally to the quantitative phenotype.
The contribution from environment may vary widely in space and time, and hence
also the proportion of the total phenotypic variation that is genetic. Despite the
fact that the phenotypic variation is variable and continuous, it is firmly established
that quantitative genetic variation as a phenomenon is consistent with Mendel's
laws, and Fisher (1918) demonstrated mathematically that the inheritance of
quantitative traits can be explained by Mendelian inheritance at multiple
polymorphic loci.
3
BI3010H07
Halliburton chapter 13
In order to quantify the genetic part of total phenotypic variation, we must find
ways to separate the genetic part from the environmental effects (Fisher helped
us out here). Furthermore, for understanding evolution, we would want to know
how quantitative genetic variation is maintained in the populations. This involves
knowledge about the importance of factors like mutation, linkage, epistasis, and
pleiotrophy, and their role in the evolution of quantitative traits. Many of these
questions are analogues of those asked for qualitative traits in previous
chapters.
13.1 Genetic and Environmental Effects on Quantitative Traits
In an early experiment studying parent-offspring relations for seed weight in
inbred lines of beans (NB! this was before Fisher's (1918) work), Johannsen
(1903) noted a clear parent-offspring relation among inbred lines, but no
consistent parent-offspring relation within lines (Fig. 13.1 a,b). This experiment
thus demonstrated that there was a genetic factor G (variation among genetically
different lines), as well as an environmental factor E (variation among offspring
within lines, independent of parental performance).
P=G+E
4
BI3010H07
Halliburton chapter 13
13.2 The Genetics of Quantitative Characters
Consider a simple polymorphism and its observed phenotype performance
Genotype
Mean weight (Phenotypic value)
A1A1
14 g
A1A2
12 g
A2A2
6g
The midpoint between highest (A1A1) and lowest (A2A2) weight is 10g.
Let a and -a be the deviations from this value for A1A1 and A2A2.
Let d be a measure of dominance for the heterozygote, measuring the deviation from
the mid-value of 10 for the heterozygote. (cf Fig. 13.5 next slide). Now;
Genotype
Value
Frequency
A1A1
a(=4)
p2
A1A2
d(=2)
2pq
A2A2
-a ( = - 4 )
q2
5
BI3010H07
Halliburton chapter 13
Halliburton Fig. 13.5 p. 533
Illustration of genetic effects
6
BI3010H07
Halliburton chapter 13
With this information, the mean value ( ) of the entire population can be found as the
weighted average of a, d and -a (weighted by the genotypic frequencies):
µ = p2a + 2pqd + q2(-a), i.e.
µ = a(p-q) + 2pqd
(13.2)
Having found the population mean µ, the genotypic value G of each genotype can be
expressed by its deviation from the this value.
G11 = a - µ
G12 = d - µ
G22 = -a - µ
In combination with (13.2) this gives:
G11 = 2qa - 2pqd
G12 = a(q-p) + d(1-2pq)
G22 = -2pa - 2pqd
(13.3)
(13.4)
(13.5)
The genotypic values G are measures of how superior or inferior the average of each genotype is
compared to the population mean. Therefore these values depend on the allele frequencies.
!! Note that the genotypic value is not the same as the breeding value (next slide).
7
BI3010H07
Halliburton chapter 13
Decomposition of the Phenotype
The phenotype of an individual is determined to some degree by its genotype.
However, in sexual reproduction, the genotypes of the parents are broken up during
the Mendelian segregation, so that each parent transmits only one allele to the
offspring. Therefore, we need some measure of the average value of an allele when
it combines at random with other alleles in the population (its breeding value).
Consider allele A1. Under random union of gametes it will combine with another A1
with a frequency of p. Likewise, it will combine with an A2 with a frequency of q.
The resulting genotypes A1A1 and A1A2 have values of a and d, respectively, and
the average value of A1-containing genotypes will be:
µ1 = pa + qd which, expressed as (⍺), the deviation from the population mean is
⍺1 = µ1 - µ = [pa + qd] - [ a(p-q) + 2pqd]
⍺1 = q[a + d(q-p)]
(13.6)
⍺1 is called the average effect of A1.
Sililarly, the average effect of A2 is:
⍺2 = - p[a + d(q-p)]
( 13.7)
8
BI3010H07
Halliburton chapter 13
If we call the quantity in the brackets (a + d(q-p)), which are the same for both
alleles, for ⍺ (the deviation from the population mean)
⍺ = (a + d(q-p))
(13.8)
without a subscript, we can express ⍺1 and ⍺2 as:
⍺1 = q⍺
and
⍺2 = -p⍺
We now define the breeding value (BV) of an individual as the sum of the average
effects of the two alleles it carries
BV11 = ⍺1 + ⍺1 = ⍺ * 2q
BV12 = ⍺1 + ⍺2 = ⍺ * (q-p)
BV22 = ⍺2 + ⍺2 = ⍺ * -2p
Because the breeding value of an individual is the sum of the average effect of the alleles, it is
often called the additive effect and symbolized A, with subscripts to indicate the genotype. Thus,
the additive effects of the three genotypes are, also
A11 = ⍺1 + ⍺1 = ⍺ * 2q
A12 = ⍺1 + ⍺2 = ⍺ * (q-p)
A22 = ⍺2 + ⍺2 = ⍺ * -2p
(13.9 )
(13.10)
(13.11)
9
BI3010H07
Halliburton chapter 13
The breeding values (13.9–11) are not the same as the genotypic values unless d=0
(i.e. no dominance). Expressing 13.3-13.5 in terms of ⍺ the effect of allele interaction
(dominance, D) for the three genotypes can be singled out as
D11 = -2q2d
D12 = 2pqd
D22 = -2p2d
These D's are called the dominance deviations. Thus, if dominance is involved in addition
to additive effects, the genotypic values of individuals can be partitioned into
G11 = A11 + D11
G12 = A12 + D12
G22 = A22 + D22
All these quantities are expressed as deviations from the population mean. In breeding, only the
additive effects can be utilized. If the trait is influenced by many polymorphic loci, there is a
possibility of epistasis (interaction of genes at different loci) between them, symbolised by I. In
the equiation on slide 3 (P = G + E), we can now add the following detail:
P = (A + D + I) + E
(13.20)
Thus, the phenotype of an individual is due to a genetic component and an environmental
component. The genetic component can be partitioned into an additive effect from the actual
alleles, a dominance effect, and an epistasis effect. How can we make practical use of this? In
order to make progress we must study variation within the population.
10
BI3010H07
Halliburton chapter 13
"Statistical genes"
Before embarking on the description of mathematical tools in quantitative genetics, it must
be emphasized that its treatment of phenotypic variation is based on a set of important
assumptions.
First, it is more or less an axiom that each trait is controlled by a large number of unlinked
loci, each of which has a small effect on the phenotype. If so, we can, via the central limit
theorem, assume that the trait is approximately normally distributed.
We also assume that the environmental effects are normally distributed with a mean
effect of zero, so that the phenotypic mean will be equal to the genotypic mean.
Under these assumptions we can analyse quantitative characteres with the pure statistical
tools of the attractive normal distribution, and ignore the underlying genetical complexities.
Variance components for quantitative traits
If we describe the phenotype of an individual by P = G + E, the variance in the population is
described by
VP= VG + VE + 2cov(G,E)
Under the (strict) assumption that there is no (genotype x environment) interaction, the
covariance term is zero, and the phenotypic variance is divided in a genotypic and an
environmental component. The total phenotypic variance is easily obtained by
measurements, but we need some way to estimate how much of this variation is due to
genetic variation in the population. This is, of course, important in breeding programs.
11
BI3010H07
Halliburton chapter 13
Focusing first on the genetic component (VG) for a single locus trait (thus epistasis is excluded):
VG = VA + VD
We recall the variance of a random variable X is calculated as:
Var(X) = Σ fi (Xi – µ)2
where fi is the frequency of the ith values of X.
Thus, if the X'es are genotypes, the genotypic variance depends on the genotypic distribution
at the locus. Under HW equilibrium we can express genotypes by allele frequencies, and we
can write:
VG = p2(G11)2 + 2pq(G12)2 + q2(G22)2
Using our former expressions for G (eq. 13.12-13.14) in this equiation, and using ⍺, the deviations
from the population mean (µ) we arrive after a much algebraic simplification at:
VG = 2pq⍺2 + (2pqd)2 where ⍺ stands for additive effects and d for dominance effects
Thus, we define:
----------------------------------------------------------------------------------------------------------------------------------VA = 2pq⍺2
(the additive genetic variance)
13.21
and
VD = (2pqd)2
(the dominance variance)
13.22
----------------------------------------------------------------------------------------------------------------------------------If considering more than one locus for a trait, epistatic effects (VI) must be incuded, so that:
VG = VA + VD + VI
(still assuming all covariances =0)
Finally, adding the environmental effects (VE), the total phenotypic variance can be decomposed into:
VG = VA + VD + VI + VE
(assuming all covariances=0, and no genotype x environment interaction).
12
BI3010H07
Halliburton chapter 13
Heritability
After having partitioned the total pheotypic variance into a genetic and an environmental
component, we can determine the proportion due to genetic variation. This ratio is called the
"Broad Sense Heritability":
H2 = VG / VP
Similarly, the ratio of the additive genetic variance to the total phenotypic variability is called the
Narrow sense heritability:
h2 = VA / VP
The narrow sense heritability, in which dominance and interaction effects are not included, is
useful in animal breeding programs. In plant breeding, the broad sense heritability is useful
because there, entire genotypes including dominance and interaction effects can be replicated by
asexual propagation.
The exponential (2) in the heritability measures is historical and reflects that the heritabilty is a
ratio of variances (which in turn are based on squared deviations from the mean).
13
BI3010H07
Halliburton chapter 13
BOX 1. Repetition of how to compute a simple linear regression
Variances and covariances, which are heavily used in quantitative genetics, are also basis for a very common tool for assessing the
relations between variables, known as regression analysis. In its simplest form, linear regression, the computation steps are
straightforward. Note that in regression, the value of one of the variables (Y) are dependent on the value of the other (X). [If no such
dependence we perform correlation analysis].
Consider two variables X and Y for which we have a list of 4 corresponding data points. We want the
constants a and b in the formula for the best-fit straight line through these data point: Y = a + bX. ---------
>
X-values:
1
2
3
4
------------------------------------------------------------------------------------------Y-values:
3.2
7.4
8.7
12.1
We first calculate the basic terms:
n (# of data points) = 4
Σ X = 10
Xmean = 2.5
Σ X2 = 30
Σ (X)2/n = 100/4=25
a = Y intercept
b = slope of line
Σ Y = 31.4
Ymean = 7.85
Σ XY=92.5
then fill in the computational formula; lowercase x and y are
respective deviations from mean X and mean Y
11
Σ x2 = Σ X2 - Σ (X)2/n = 30 – 25 = 5
Σ xy = Σ XY – (Σ X Σ Y)/n = 92.5 – (10x31.4)/4 = 14
6
b = Σxy / Σx2 = 14/5 = 2.8
a = Ymean - b Xmean = 7.85 – (2.8x2.5) = 0.85
1
1
Thus the equation is: Y = 0.85 + 2.8X
2
3
4
------------------------------------------------------------ >
14
BI3010H07
Halliburton chapter 13
Covariance between relatives
A parent gives half of its alleles to each offspring. Hence full-sibs share ½ of their alleles with each
other, half-sibs share 1/4, and grandparents and grandchildren also ¼.
For quantitative characters which are heritable, we would thus expect close relatives to be more
similar than distant relatives or unrelated individuals in the population.
The genetic similarity among relatives is fundamental in quantitative genetics and breeding
genetics. Similarity is expressed as a covariance.
cov(X,Y) = Σ fi (Xi – EX)(Yi – EY) for all XY pairs
where fi is the frequency of the ith XY pair, and E = expected value = (weighted) mean value = µ
-----------------------Under some strict assumptions (i.e. that environmental effects are random and independent of genotype), the
phenotypic covariance equals the genotypic covariance:
cov(XP,YP) = cov(XG,YG)
The covariances between relatives are simple
fractions of VA and VD. (Table 13.5 ---->).
The degree of phenotypic resemblence between
relatives can be used to estimate the heritability h2
of a trait.
Remember from Box 1 above that the magnitude of the
covariance term between the variables determined the
slope in the linear regression.
In a regression of e.g. offspring on mid-parent the slope
of the regression line is an estimate of the heritability h2
(Fig. 13.6 on next slide).
15
BI3010H07
Halliburton chapter 13
Hence, in setting up an experiment
to estimate heritability of a trait, we
can utilize our knowledge of the
genetic similarities and expected
covariance between relatives (Table
13.5).
For example, we can perform a large
number of crossings between pairs
of parents with known individual
performance for a specific trait.
From each crossing we then
measure the performance of the
pertinent offspring (i.e. the family
groups) for the trait under study.
In a regression of offspring (O)
performance on mid-parent (P)
(cov(O,P)= ½ VA) performance, the
slope of the regression line estimates
the narrow sense heritability h2 of the
trait under the given environmental
conditions (Fig. 13.6 ---->).
16
BI3010H07
Halliburton chapter 13
13.3 Artificial selection on a
quantitative trait.
Truncation selection
is based on a ranking of individuals based
on their measured phenotypic performance.
Phenotypes above a chosen truncation point
are selected to be parents of the next
generation. (See graphs in figures 13.7 and
13.8).
( --------------------------------------------->).
Whether this will lead to a genetic
improvement of the breeding stock depends,
e.g., on the heritability of the trait; h2 (page
543); the ratio of additive genetic variance to
phenotypic variance VA/VP.
An equivalent meaning of the heritbility is
the regression of breeding value (A) on
phenotypic value (P):
h2 = bAP
(if we use knowledge of genetic similarities
among full- or half-sibs as basis for
estimating heritability of traits, we speak
about correlation anaysis, not regression
analysis.
17
BI3010H07
Halliburton chapter 13
BOX 2. Heritability
By regarding the heritability as the regresssion of breeding value (VA; the additive variance
component) on phenotypic value we see that an individual's estimated breeding value is the product
of its phenotypic value and the heritability:
A(expected) = h2P
where breeding values and phenotypic values are both reckoned as deviations from the population
mean. The heritability enters into almost every formula connected with breeding methods, and
many practical desicions about procedures depend on its magnitude. The determination of
heritability is one of the first objectives in the genetic study of a metric character.
It is important to realize that the heritability is a property not only of a character but also of
the population and of the environmental circumstances to which the individuals are
subjected. Since the value of the heritability depends on the magnitude of all the
components of variance, a change in any one of these will affect it. All the genetic
components are affected by gene frequencies and may therefore differ from one population
to another, according to the past history of the population. In particular, small populations
maintained long enough for an appreciable amount of fixations to have taken place are
expected to show lower heritabilities than large populations. The environmental variance is
dependent on the conditions of culture or management: more variable conditions reduce the
heritability; more uniform increase it. So, whenever a value is stated for the heritability of a
given character it must be understood to refer to a particular population under particular
conditions.
Empiri has shown that in general, traits important for fitness have lower heritabilities than 18
other, less important traits.
BI3010H07
Halliburton chapter 13
Some definitions:(cf Fig. 13.7 --->)
Selection differential (S) = the difference
between the mean of the parental population and
the mean of the individuals selected for breeding.
Selection intensity (I) = S measured in SD units.
Selection response (R) = the difference between
the mean of the parental generation and the
mean of the offspring from the individuals
selected for breeding.
Breeder's equation:
The regression of offspring value on midparent
value in Fig. 8 is basis for a reasoning of the
author from which he arrives at some very
important connections between S and R above,
e.g. that the heritability is equal to the ratio R/S,
and from there to what is known as the breeder's
equiation:
R = h2S
because it can be used to predict the response to
directional selection on a quantitative trait.
19
BI3010H07
Halliburton chapter 13
Using the breeder's equiation: R = h2S
Commonly in quantitative genetics, traits are
normally distributed and subgroup
characteristics measured as deviations from
population mean. (in SD units).
In practical implementations of the breeder's
equiation, Falconer's Table A is widely used.
It contains a compilation of values of p (the
percentage of the population above a specific
truncation point T), x, the value of T in SD
units, and i; the mean value (in SD units) of
individuals with values exceeding T.
For example, if the truncation point T is chosen
so that group selected for breeding is the best
20% of the distribution, its corresponding value
in SD units (x) is 0.842, and the mean value of
the individuals exceeding T is 1.4 SD units.
cont'd next slide
20
BI3010H07
Halliburton chapter 13
breeder's equiation cont'd
In the breeder's equiation R = h2S, (NB! one generation) the selection differential S can be written as
S = I * SDP,, so that the breeder's equiation can also be written as
R = h2 * I * SDP
where I = the selection intensity (the difference in mean value between population mean and the
selected group, measured in SD units (of population mean), and SDP is the standard deviation of the
population's phenotypic mean value.
A practical example:
Consider a farmed salmon breeding population in which a breeding program for increased body
growth is started. Assume that the mean weight of the two-years old salmon constituting the parental
population is 1kg with an SD=0.4 kg, and let the heritability for this trait be h2=0.30. The best 2.4% of
the population is used to produce the next generation. What is the expected increased mean weight
among the offspring when they reach two years of age?
The truncation T point which corresponds to the upper 2.4% of the population lies ~1.98 SD units
above the population mean (Table A), that is (1.98x0.4kg) 0.79 kg above. Hence all individuals
heavier than 1.79 kg were used as a brood stock. These individuals have a mean weight which
according to Table A is 2.35 SD units above the population mean; i.e. (2.35x0.4) = 0.94 kg above.
Thus the selection differential (S) is 0.94 kg, and R = h2*S = 0.28
The expected mean weight of two years old individuals in the offspring will be: 1.28 kg.
21
BI3010H07
Halliburton chapter 13
Response to repeated selection
(general observations)
Short term response:
1. Response constant short term
2. Thereafter a plateau
3. When relaxed, the gain is reduced
4. Response up/down assymmetrical
5. Viability/fertility reduced over time
Long term response:
1. plateau reached (Fig. 13.9c -->)
2. Causes: Genetic drift and selection
changes variability and allele freq.
The genetic drift effect:
Ht = H0 [1 - 1/(2N) ] t
an analogous formula for additive genetic
variance is
VA(t) = VA(0) [1 - 1/(2N) ] t
22
BI3010H07
Halliburton chapter 13
Response to repeated selection
(cont'd)
Results from short-term selection
(5 generations) for increased cholesterol
level in mice (Table 13.6 and Fig. 13.10).
The slope of the regression line in Fig.
13.10 is an estimate of the realised
heritability. The respons is fairly constant
over 5 generations.
23
BI3010H07
Halliburton chapter 13
Correlated response to selection:
Frequently, selection for one trait can affect another trait, because of genetic correlations between
traits. Genetic correlations can be due to pleiotrophy (one gene affects more than one trait) or
gametic disequilibrium (alleles at a locus affecting one trait is in gametic disequilibrium with alleles
at a locus affecting another trait e.g. due to linkage).
The correlation coefficient (r) between two random variables is defined as:
r = cov(XY) / (σXσY ), where σX and σY are the standard deviations (SD) of X and Y.
13.42
Genetic correlations (covariance) have two components, a genetic correlation and an environmental.
The environmental correlation is due to milieu factors affecting both traits simultaneously. Hence
rP = hXhYrA + eXeYrE
(derived in Box 13.2)
13.43
The response in Y (RY) when selection is on trait X in the same individuals can be predicted by:
RY = rAhXhYSσPY /σPX
or equivalently because, since selection intensity i = S/ σPX ,
RY = rAhXhYiσPY
13.44
13.45
The term rAhXhY is called the coheritability
The rA is difficult to estimate, but a reasonable assumption is that rA ~ rP
NB! Correlated responses (genetic correlations) may be the main reason for reduced fitness of
24
populations under artificial selection.
BI3010H07
Halliburton chapter 13
REMINDERS:
Pleiotrophy = when a single gene influences multiple phenotypic
traits
Epistasis = when the effect of a gene at one locus is modified by
genes at one or several other loci
25
BI3010H07
Halliburton chapter 13
13.4 Natural Selection on Quantitative Traits
In nature, many quantitative traits (weight, growth rate, age at maturation, fecundity, etc) affect
fitness, and thus are almost certainly subject to natural selection.
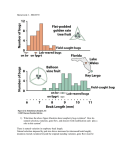
Kinds of natural selection (cf Fig. 13.11 in Halliburton)
These are the same as treated for single locus, qualitative genetic characters:
1. Directional selection (probably affects many fitness-related traits)
2. stabilizing selection (e.g. birth weight in humans)
3. Disruptive selection (importance in nat. pop. unclear)
Antagonistic pleiotrophy (Drosophila; development time vs high fecundity) can be due to negative
correlations between fitness components (p. 557).
Natural selection on correlated traits
How can we determine if natural selection acts directly on a trait, or via selection on a correlated trait?
Lande & Arnold (1983) showed how this can be done by multiple linear regression (p. 558-562). This
method has been widely used; Price et al. (1984) showed that body weight and beak depth in
Darwin's finches were under strong natural selection compared to a set of correlated morphological
traits.
The strength of natural selection
Natural selection can take a wide range of values, and overlaps extensively with the intensities
applied in artificial selection experiments (Endler 1983). Whether directional or stabilizing selection is
the most common form is under debate. (NB! Note an error in Table 13.10; in the table heading
26
subtext, "directional" should be changed to "disruptive").
BI3010H07
Halliburton chapter 13
13.5 Quatitative Trait Loci – "QTL" (loci that affect a quantitative trait)
A QTL is a relatively small region on a chromosome. It does not necessarily correspond to a
single gene; it can also consist of several tightly linked genes which are inhereted as one unit.
1. The number of loci affecting a QTL can be estimated under certain circumstances, using
the so-called Castle-Wright estimator.
2. Also, it is sometimes possible to map the genes controlling a quantitative trait (a QTL) to
specific regions on a chromosome by using a linked marker gene.
27
BI3010H07
Halliburton chapter 13
1. How Many Loci Affect a Quantitative Trait?
The Castle-Wright estimator is based on the phenotypic difference between two inbred lines
(fixed for alternative alleles at loci affecting a quantitative trait). The inbred lines are crossed,
and then the F1 are crossed with each other to produce an F2.
The mean phenotypic values for the two inbred lines are denoted by M1 and M2. The
variance in the F2 will be higher than in either inbred line or the F1.
The excess variance is called the segregational variance Vseg = VF2 – VF1.
Castle (1921) and Wright (1968) showed that an estimate of the minimum number (ne ) of
loci affecting the trait is
ne = (M1 – M2 )2 / ( 8Vseg ) (also called the effective number of loci affecting the trait)
28
BI3010H07
Halliburton chapter 13
Box 3. The Castle-Wright estimator:
ne = (M1 – M2 )2 / ( 8Vseg )
Castle (1921) and Wright (1968) deviced a method
for estimating the number of (polymorphic) loci
affecting a quantitative trait.
Basically, the method utilizes the increase in
phenotypic variance due to segregation.
The starting point is two inbed lines (fixed for
different alleles). These are crossed to get an F1
generation (all heterozygotes). Then an F1xF1 cross
is performed to get all three genotypes segregated in
the F2 generation.
The segregation in all three genotypes leads to
increased phenotypic variance for the trait in F2,
proportional to the number of segregating loci
affecting the trait.
29
BI3010H07
Halliburton chapter 13
Numeric example:
Phenotypic mean value for inbred line A: 40.0 (all homozygotes)
Phenotypic mean value for inbred line B: 20.0 (all homozygotes)
Cross AxB to produce F1
Variance in F1: 5.0 (all heterozygotes)
Cross F1xF1 to produce F2
Variance in F2: 10.0 (segregating into all three genotypes)
ne = (40.0 – 20.0)2 / 8(10.0 – 5.0) = 400 / 40 = 10 loci
30
BI3010H07
Halliburton chapter 13
Test your understanding:
Assume two populations P1 and P2 of a species, and a normally distributed trait, say
body weight at 2 years of age, which is determined by genotypes at a QTL.
P1 and P2 have been kept isolated from each other and selected for high and low weight,
respectively, for many generations. They are both assumed to be completely inbred, but
fixed for different alleles at all the loci included in the QTL.
How would you proceed to estimate the number of polymorphic loci affecting the body
weight at age 2 years?
31
BI3010H07
Halliburton chapter 13
2. Mapping Quantitative Trait Loci
The approach for estimaing the number of loci affecting a quantitative trait (above) does not reveal the
location of QTLs on the chromosome. For this purpose, a genetic mapping using marker loci with known
positions can be used. Most commonly, two different inbred lines, which are different in their phenotypic
value for a trait, are crossed. Then the resulting F1 progeny are crossed with each other to produce F2. The
segregation for a marker locus and the phenotypic values in F2 can be used to identify the location of a QTL
(in terms of number of crossing-over units from the marker). When lines that differ in both marker and QTL
are crossed, linkage disequilibrium (D') is generated between the loci; the magnitude of D' it is then used to
detect the presence and location of the QTL. The simplest approach is the "single-marker analysis":
Single-marker analysis
Assume two inbred lines that are fixed for different alleles at both a marker locus M with
alleles M1 and M2, and a quantitative trait locus Q with alleles Q1 and Q2.
Line
Genotype
Genotypic value
L1
Q1M1
a
L2
Q2M2
-a
The two inbred lines are crossed to produce F1, which are all of the same genotype Q1M1 / Q2M2,
i.e. in complete gametic disequilibrium. Then the F1 are crossed with each other to produce F2. If
the marker and the QTL are completely linked (no recombination; r = 0), the F2 combined
genotypes and their expected frequencies will be:
Genotype
Frequency
Marker genotype
Genotypic value
Q1M1 / Q1M1
0.25
M1M1
a
Q1M1 / Q2M2
0.50
M1M2
d
Q2M2 / Q2M2
0.25
M2M2
-a
32
Halliburton chapter 13
BI3010H07
Numeric example:
The data of Sax (1923) on seed weight in beans can be used as an example. Sax crossed two inbred lines of beans
which differed in both pigmentation and mean seed weight, and produced an F 1 generation. The F1 were then crossed
with each other to produce F2 (which has Mendelian segregation of alleles into different genotypes). The pigmentation
locus is here assigned two alleles P and p, with genotypes PP, Pp, and pp. The mean seed weight in the marker
genotypes of the inbred parental lines and the F2 are shown in the table below.
Group
Mean weight
Parental 1
48.0 (+a)
Parental 2
21.0 (- a)
F2
PP mean weight
Pp mean weight
pp mean weight
30.7
28.3
26.4
The difference in mean seed weight between marker homozygotic genotypes (30.7-26.4 = 4.3) accounts for only 16% of the
difference (48-21 = 27) between the parental lines but is statistically significant. Hence there is some degree of chromosomal
association (linkage) between the marker locus and some gene (QTL) affecting the quantitative trait seed weight. On the
other hand the effect is not complete, so some degree of recombination (0< r <0.5 ) must have occurred in the gamete
formation (meiosis) in F1, which broke up the initial disequilibrium between Q1 and M1, and Q2 and M2. The expected (E)
difference between the homozygous marker genotypes in F2 is :
E(M1M1) – E(M2M2) = 2a (1 – 2r)
(where r denotes the recombination rate between marker and QTL)
13.49
The equiation implies that with complete linkage (r=0) , the homozygote differences in F2 is the same as that between the
parental inbred lines. If r=0.5 (unlinked loci), the F2 homozygotes do not differ for the QTL trait, i.e. the marker alleles are
randomly associated with the QTL alleles.
In the bean data of Sax (above), the observed difference in mean weight between parental lines was (48-21) = 27 cg. The
difference between marker homozygotes was not nearly as big (30.7 - 26.4) = 4.3 cg, suggesting that the marker locus is not
very tightly linked to the QTL. Putting in the F2 marker homozygote difference (4.3) on the left-hand side in (13.49), and the
parental line difference (27) in for 2a on the right-hand side yields r = 0.42, i.e. the marker locus and the QTL are 42 map
33
units (µ), or 42 cM, apart from each other on the chromosome (see centiMorgan definition next page) .
BI3010H07
Halliburton chapter 13
Definition of centiMorgan:
One centiMorgan is defined as the genetic distance between two loci with a statistically
corrected recombination frequency of 1%; the genetic distance in centiMorgans is numerically
equal to the recombination frequency expressed as a percentage. Symbol, cM. The
centimorgan is now more commonly called a “map unit” (symbol, mu) or Locus Map Unit
(symbol, LMU).
The qualification “statistically corrected” is necessary because at "genetic distances" greater
than about 7 cM, the relationship between recombination frequency and genetic distance is no
longer linear. Researchers have developed mathematical models that can correct for this
difficulty.
The centimorgan is not a measure of physical distance, but typically a genetic distance of 1 cM
corresponds to a physical distance of roughly one million base pairs. Attempts to assign a
physical length to the centimorgan have led to an estimate that it is roughly about 0.003
millimeters.
34
BI3010H07
Halliburton chapter 13
The backcross method
In QTL mapping, an alternative to the
crossing of F1 with each other, is to
cross F1 with one of the inbred parental
lines. This procedure saves one pure
parental chromosome all the way to the
F2 generation, and is the simplest one
available. The statistical methods used,
and the statistical issues that arise, are
largely the same for all the different
types of crosses. However, the
backcross has the advantage of
simplicity; at each locus in the genome,
the backcross progeny have one of only
two possible genotypes (genetic
composition). The procedure is outlined
in the figure to the right.
35
BI3010H07
Halliburton chapter 13
QTL in Humans and Natural Populations
The study of completely inbred lines outlined above is not possible in humans and natural populations, hence
alternative approaches must be used. In humans the necessary information about gametic stage disequilibrium
must be inferred from pedigree data, which is too slim in many families. Also, sample sizes are usually small,
resulting in low statistical power. Lynch & Walsh (1998) review techniques developed for use on humans and other
outbred populations.
13.6 Evolutionary Quantitative Genetics
Quantitative genetic descriptions and predictions in natural populations must consider long-term evolutionary
processes. This means that the many simplifying assumptions which was reasonable when exploring short-term
effect, cannot be made for long-term processes. Thus, effects from dominance, pleiotrophy, epistasis and
mutations cannot be overlooked, they may be important players on the evolutionary scene.
For answering the question "How much genetic variation for quantitative traits is there in natural populations?" one
must examine the predicted effects of those evolutionary forces that are responsible for genetic differentiation,
namely:
1. natural selection
2. mutation
3. genetic drift
The effect of natural selection on genetic variation
Stabilising selection (in the multilocus sense) will decrease the phenotypic variance, but it is less certain whether
this means a decrease in the genotypic variance. (cf text page 573 upper part). Roff (1977) reported that most
models suggest that additive genetic variance will decrease in response to stabilising selection.
Directional selection will also tend to reduce additive genetic variance.
Disruprive selection is more uncertain in this respect. Most models suggest that genetic variance will increase
over the short-term, but the long-term effect is unclear (cf Fig. 13.19 w/text).
Presently, the consensus is that most forms of natural selection should cause a long-term decrease in genetic
variance; not unsimilar to the expectations in artificial selection regimes.
36
BI3010H07
Halliburton chapter 13
Heritabilities in natural populations
It is widely believed that fitness-related traits (viability, fertility) are under stronger natural selection than e.g.
morphological traits, and hence that life history characters should have less additive genetic variation (i.e. lower
heritability) than morphological characters. This prediction has been confirmed (cf Table 13.14) p. 574), but life history
trait heritabilities are not zero! Furthermore, laboratory experiment estimates of heritability may be overestimates
relative to those in natural populations because of a lower environmental component in captive populations. Also,
possible (genotype x environment) interaction in nature may be underestimated in the laboratory. Looking away from
this, however, heritability estimates from laboratory and natural populations are not significantly different. Hence
heritabilities stemming from laboratory estimates may be good proxies for those in natural populations (but see below).
Heritability vs additive genetic variance
Estimated heritability may not always be a good surrogate for additive genetic variance, because other genetic
variance components ("residual variance”; cf slide 12) than VA may be substantial. Houle (1992) suggested that the
Coefficient of additive genetic variation CVA is better for comparing variation between traits.
CVA = SQRT[VA ] / µ x 100, and
CVR = SQRT[VP – VA ] / µ x 100
(R denotes residual and µ =population mean )
CVA and CVR has been shown to be higher for fitness-related traits than for morpholocical traits. Also, h2 and CVR
appear to be negatively correlated. This suggest that the lower heritabilities of fitness-related traits may be due to high
amounts of residual genetic variance, which is different from the view that it is due to lower amounts of additive
genetic variance.
Mutation rates for quantitative characters
There is currently uncertainty concerning mutation rates for quantitative characters, due to apparent overestimates
from available models. Cf text p. 579 ff.
37
BI3010H07
Halliburton chapter 13
Effects of mutation and genetic drift on genetic variance
Mutations create new alleles each generation, which will increase the genetic variance for a trait. The amount of genetic
variance created by mutations each generation is called mutational variance (VM) and will add to the additive genetic
variation each generation by:
VA(t+1) = VA(t) + VM
The value of VM depends on the number of loci mutating, the mutation rate per locus, and the phenotypic effect of a
mutation.
Joint effects of mutation and natural selection on genetic variance
Theoretical models for exploring this have not yielded consistent results. Very much, the conclusions depend on the
validity of assumptions made for the models. Caballero & Keightly (1994) analyzed some complex models including
dominance and pleiotrophy effects of mutations on viability, and various distributions of the effects of mutation on the
quantitative trait and fitness.The main 6 conclusions they drew are liste in Halliburton p. 583-584.
How inportant are dominance, linkage, epistasis and pleiotrophy?
Recent advances in molecular and statistical techniques have allowed the examination of fundamental assumptions of
the basic quantitative genetics model. Shortly told, all of these assumptions are violated to a greater or lesser degree.
This may have little effect on short-term predictions, but demands a re-examination of long-term predictions. Mackay
(2001) gives an overview of the status on this topic.
What maintains genetic variation for quantitative traits?
Contrary to most theoretical predictions, genetic variation for quantitative traits is common in natural populations. There
is a long list of possible explanations, but we do not know which is correct. Recent approaches using molecular marker
loci and powerful statistical techniques may suggest a rapid progress in this scientific field.
38
BI3010H07
Halliburton chapter 13
39
BI3010H07
Halliburton chapter 13
40