Download Physics 535 lecture notes: - 7 Sep 25th, 2007 Reading: Griffiths

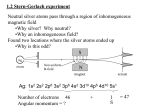
Physics 535 lecture notes: - 7 Sep 25th, 2007
Reading: Griffiths Chapter 4
Homework: Griffiths: 3.4, 3.14, 3.15(a), 3.16(a), 3.17(a,d)
1) Introduction Symmetries
Many symmetries that we observe in nature are associated with conservation laws.
Some Examples:
Time invariance: Energy
Translation invariance: Momentum
Rotational Invariance: Angular Momentum
Gauge Transformation: Charge
Time invariance and energy conservation is interwoven in the way we treat quantum
mechanics using a Hamiltonian or more typically a Lagrangian. The time dependent
Schrödinger equation contains this explicitly.
d 2 (x,t)
d(x,t)

 U(x)(x,t)  i
2
2m dx
dt
2
H(x,t)  i


d(x,t)
 (x,t)  E(x,t)
dt
Solutions of the Schrödinger equation
(x,t)   (x)e it
Had a constant, or conserved property  that we identified with the energy.



For a charge consider a wave-function  undergoing the gauge transformation   ei
and antiparticle bar  e-ibar. If we treat this as a infinitesimal transformation,  
(1+i). Then:
0  L
L
L
 
 (  )  anti

 ( ) 
0  L
L
L
(i ) 
 (i )  anti

 ( )
Inserting the other side of a differentiation by parts
 L 
L
L 
0  L   
  i 
 (  ) 
  anti
( )

  

The first term is the Euler-Lagrange equation, which equals 0.
  L 
 L  
0  L i   




 
 (  ) 
 ( ) 







 


but this is the equation for a conserved current

 j   0
Q
 d xj
3
0
 const
Note that the inclusion of the antiparticle in this conserved current.

Often these kinds of symmetries are categorized by group theory. The gauge
transformation is a unitary transformation in one dimension, U(1). The transformation
can also be represented as a matrix, very simple in one dimension. There are many group
transformations we encounter in particle physics
U(n) Unitary transformation in n dimensions, nxn matrix, UU+, U+ transpose conjugate.
SU(n) Special transformation in n dimensions, nxn matrix with determinant 1.
O(n) Orthogonal transformation in n dimensions, nxn matrix. O transpose and inverse are
the same.
SO(n) Special orthogonal transformation in n dimensions, nxn real matrix with
determinant 1.
U(1) Gauge symmetry and conservation of charge
SU(2) spin and isospin symmetry and conservation
SO(3) rotational symmetry and conservation of angular momentum, same SO(3) except
for a minus sign. Thus the same in probabilities, which is why we combine them later.
Aside from charge conservation angular momentum conservation and spin conservation
are very important in quantum electrodynamics. The particles that we deal with will have
spin and will obey conservation of spin and angular momentum. In fact we will have to
include spin explicitly in our wave equations for particles. Also often spin and angular
momentum are combined together into a combination conservation of total angular
momentum. For instance for a planet rotational angular momentum around the sun and
spin angular momentum around the axis have to be simultaneously conserved. Similarly
spin angular momentum s, orbital angular momentum l have to be combined into total
angular momentum and conserved.
Since this is a quantum system, with all states quantized spin and angular momentum will
be conserved as well. If we think back to the hydrogen atom it could be thought of a
particle in a box in three dimensions and thus had 3 quantum numbers. Instead of x, y
and z quantum numbers since there is spherical symmetry the solution has radial, n, total
angular momentum, l, and the projection of the angular momentum on the z axis, ml,
quantum numbers. Note that total angular operator L2 yields an angular momentum of
l(l+1)hbar2. The Lz quantum number gives projection mlhbar
These quantum numbers run from l=0,1…n-1 and ml=-l,…-1,0,1…l. The last quantum
number can be thought of as running from pointing along the z axis to pointing along the
negative z axis.
The spin quantum can be integer or half integer, integer for bosons and half integer for
fermions. Similarly ms runs from =-s,-s+1,…,s-1,s, skipping 0 for fermions. Usually
spin quantum numbers for individual particles are only s=0,1/2,1. Though we believe
that the graviton is probably spin 2.
The spin states, quantum numbers and operators can be though of as vectors and
matrices.
Lets write the eigenvectors of spin up and down particles as orthogonal vectors. A real
particle can be in some arbitrary combination of these until we measure it at which point
it will have some probability to be in either state.
10
    , 
01
  1 0
      
  0 1

We can then write two operators that the  vectors will be eigenvectors of and have
specific eigenvalues.
1 0 
Sz  

2 0 1
0 1
0 i
S 2  Sx2  Sy2  Sz2,Sx  
, Sz  

2 1 0
2 i 0 

SU(2) transformation matrices
Note that Sz gives eigenvalues of (1/2)hbar and (-1/2)hbar. Also even the arbitrary
combination is still in an eigenstate of S2, s(s+1)hbar2.
Combination angular momentum is an operation that can be very important for various
interactions. For instance, if you bind two quark together into a meson you start with two
particles with spin angular momentums and combine them into one particle with a total
spin angular momentum. The initial state is clearly in eigenstates of the the two separate
spins while the final state is in an eigenstate of the combined spin. To find out what final
states we produce with what probabilities we need to understand how to express one set
of eigenstates as a linear combination of the other states. This sort of problem may
happen involving just spins or possibly orbital angular momentums as well. For instance
if a photon impacts the 2 quark system and is absorbed it’s spin angular momentum of 1
would be added to the system possibly bumping it up to a higher orbital angular
momentum state just as in an atom. Though in the case of particles these spin and
orbital angular momentum states are so energetic that we refer to them as different
particles.
To add angular momentums:
1) The z components simply add m=m1+m2
2) The j(or l,s) components may be aligned j=j1+j2, opposite, j=|j1-j2| or anywhere
inbetween, j=|j1-j2|,|j1-j2|+1…j1+j2.
The coefficients that determine the probability of each state are called the ClebschGordan coefficients and can be looked up in the particle databook.
In the case of combining quarks.
|s,m>=|s1,m1>|s2,m2>
|1,1>=|1/2,1/2>|1/2,1/2>
|1,0>=(1/2)(|1/2,-1/2>|1/2,1/2>+|1/2,-1/2>|1/2,1/2>)
|1,-1>=|1/2,-1/2>|1/2,-1/2>
vector mesons – symmetric wave function
|1,0>=(1/2)(|1/2,-1/2>|1/2,1/2>-|1/2,-1/2>|1/2,1/2>)
pseudoscalar mesons – antisymmetric wavefunction
Given an arbitrary combination of original spin states you can get either type of meson.
This is useful if you want to produce a specific type a meson. You can used polarized
electron beams to produce them via pair production and annihilation for instance.