Download MASSACHUSETTS INSTITUTE OF TECHNOLOGY

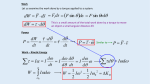
MASSACHUSETTS INSTITUTE OF TECHNOLOGY
Department of Physics
Physics 8.01
IC-W11D3-3 Group Problem 3 Sections L05-07
A bowling ball of mass m and radius R is initially thrown down an alley with an initial
speed v0 and backspin with angular speed  0 , such that v0  R  0 . The moment of
inertia of the ball about its center of mass is Icm  (2 / 5)mR2 . Your goal is to determine
the speed vf of the bowling ball when it just starts to roll without slipping. What is the
speed vf of the bowling ball when it just starts to roll without slipping?
Solution: We begin by coordinates for our angular and linear motion. Choose an angular
coordinate  increasing in the clockwise direction. Choose positive kφ unit vector
pointing into the page. Then the angular velocity vector is defined to be a
r
d φ
   z kφ 
k
dt
and the angular acceleration vector is defined to be
r
d 2
   z kφ  2 kφ .
dt
i unit vector pointing to the right in the figure. Then the velocity of
Choose the positive φ
the center of mass is given by
dx
r
v cm  vcm,x φ
i  cm φ
i
dt
and the acceleration of the center of mass is given by
d 2 xcm φ
r
φ
a cm  acm,x i 
i.
dt 2
The free body force diagram is shown in the figure below.
r
r
i and  0   0kφ . The velocity of a point
At t  0 , when the ball is released, v cm,0  v0 φ
on the rim of the wheel that is in contact with the ground is then
r
r
r
v contact ,0  v cm,0  v tan,0  (v0  R 0 )φ
i
(1)
so the wheel is sliding forward with respect to the ground and hence the friction force on
i -direction.
the wheel opposing the motion is kinetic friction and acts in the negative φ
Our “rule to live by” for rotational motion is that
r
r ext dL S
S 
dt
(2)
In order for angular momentum about some point to remain constant throughout the
motion, the torque about that point must also be zero throughout the motion.
Recall that the torque about a point S is define as
r
r
r
 ext
  rS ,i  Fiext
S
i
r
r
where rS ,i is the vector form the point S to where the ith force Fiext acts on the object. As
the ball moves down the alley, the contact point will move, but the friction force will
always be parallel to the line of contact between the bowling bowl and the surface. So, if
we pick any fixed point S along the line of contact between the bowling bowl and the
surface then
r
r
r
r
 S , f  rS , f  fk  0
k
k
r
r
because rS , f and f k are anti-parallel. The gravitation force acts at the center of mass
k
hence the torque due to gravity about the point S is
r
r
r
 S ,mg  rS ,mg  mg  dmgkφ
where d is the distance from the point S to the contact point between the wheel and the
ground.
The torque due to the normal force about the point S is
r
r
r
 S , N  rS , N  mg  dNkφ
with the same moment arm d . Because the wheel is not accelerating in the φj -direction,
from Newton’s Second Law, we note that
mg  N  0
Therefore
r
r
r
 S , N   S ,mg  d(mg  N )kφ  0
Hence, there is no torque about the point S and the angular momentum about the point
S is constant,
r
r
(3)
L S ,0  L S , f
The initial angular momentum about the point S
is due to the translation of the center of mass and rotation about the center of mass
r
r
r
r
L S ,0  rS ,cm,0  mv cm,0  I cm   m R vcm,0kφ  I cm 0kφ .
(4)
The final angular momentum about the point S has both a translational and rotational
contribution
r
r
r
r
L S , f  rS ,cm, f  mv cm, f  I cm f  m R vcm, f kφ  I cm z, f kφ ,
(5)
When the wheel is rolling without slipping,
vcm, f  R z, f
(6)
and also Icm  (2 / 5)m R2 . Therefore the final angular momentum about the point S is
r
L S , f  (m R  (2 / 5)m R) vcm, f kφ  (7 / 5)m R vcm, f kφ.
(7)
Equating the z-components in Equations (4) and (7) yields
m R vcm,0  (2 / 5)m R 2 0  (7 / 5)m R vcm, f ,
(8)
vcm, f  (5 / 7)vcm,0  (2 / 7) R 0 .
(9)
which we can solve for