Physics 101 Learning Guide
... Key 6 2. If the falls are 1 meter high, what is the speed of the fish with respect to the ground when it begins to swim upward at the bottom of the falls? Key 27 3. If the falls are two meters high what is minimum height in the stream to which the fish must jump in order to be able to swim up to the ...
... Key 6 2. If the falls are 1 meter high, what is the speed of the fish with respect to the ground when it begins to swim upward at the bottom of the falls? Key 27 3. If the falls are two meters high what is minimum height in the stream to which the fish must jump in order to be able to swim up to the ...
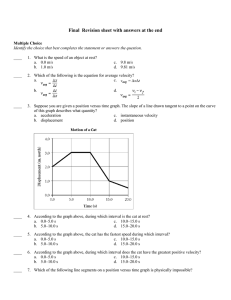
Slide 1
... Small-diameter structures would have to rotate at high speeds to provide a simulated gravitational acceleration of 1 g. Sensitive and delicate organs in our inner ears sense rotation. Although there appears to be no difficulty at 1 RPM, many people have difficulty adjusting to rotational rates great ...
... Small-diameter structures would have to rotate at high speeds to provide a simulated gravitational acceleration of 1 g. Sensitive and delicate organs in our inner ears sense rotation. Although there appears to be no difficulty at 1 RPM, many people have difficulty adjusting to rotational rates great ...
final exam - PHYSICS57
... 1. At the instant when the traffic light turns green, an automobile starts with a constant acceleration of 1.8 m/s2. At the same instant a truck travelling with a constant speed of 8.5 m/s overtakes and passes the automobile. (a) How far beyond the starting point will the automobile overtake the tru ...
... 1. At the instant when the traffic light turns green, an automobile starts with a constant acceleration of 1.8 m/s2. At the same instant a truck travelling with a constant speed of 8.5 m/s overtakes and passes the automobile. (a) How far beyond the starting point will the automobile overtake the tru ...
Instruction Manual/Experiments Guide
... In this lab, a small mass m will be connected to the Dynamics Cart by a string as shown in Figure 3.1. The string will pass over a pulley at the table’s edge so that as the mass falls the cart will be accelerated over the table’s surface. As long as the string is not too elastic and there is no slac ...
... In this lab, a small mass m will be connected to the Dynamics Cart by a string as shown in Figure 3.1. The string will pass over a pulley at the table’s edge so that as the mass falls the cart will be accelerated over the table’s surface. As long as the string is not too elastic and there is no slac ...
Chapter 10
... (e) Evaluating the expression in part (d) at t = 4 s yields 4 = 18 rad/s2. We note that our answer for avg does turn out to be the arithmetic average of 2 and 4 but point out that this will not always be the case. 7. (a) To avoid touching the spokes, the arrow must go through the wheel in not mo ...
... (e) Evaluating the expression in part (d) at t = 4 s yields 4 = 18 rad/s2. We note that our answer for avg does turn out to be the arithmetic average of 2 and 4 but point out that this will not always be the case. 7. (a) To avoid touching the spokes, the arrow must go through the wheel in not mo ...
Solutionbank M1 - solution banks
... Two men, Eric and Fred, set out to carry a water container across a desert, using a long uniform pole. The length of the pole is 4 m and its mass is 5 kg. The ends of the pole rest in equilibrium on the shoulders of the two men, with the pole horizontal. The water container has mass 16 kg and is sus ...
... Two men, Eric and Fred, set out to carry a water container across a desert, using a long uniform pole. The length of the pole is 4 m and its mass is 5 kg. The ends of the pole rest in equilibrium on the shoulders of the two men, with the pole horizontal. The water container has mass 16 kg and is sus ...
Foundation - Physics Instructor Guide
... At the completion of this training session, the trainee will demonstrate mastery of this topic by passing a written exam with a grade of ≥ 80 percent on the following Terminal Learning Objectives (TLOs): 1. Convert between units of measure associated with the English and System Internationale (SI) m ...
... At the completion of this training session, the trainee will demonstrate mastery of this topic by passing a written exam with a grade of ≥ 80 percent on the following Terminal Learning Objectives (TLOs): 1. Convert between units of measure associated with the English and System Internationale (SI) m ...
MECN 4600 Inter
... It is defined by the work done in moving a particle from one point to another that is independent of the path followed by the particle. Two examples are weight of the particle and elastic force of the spring. Potential Energy: It is the measure of the amount of work a conservative force will ...
... It is defined by the work done in moving a particle from one point to another that is independent of the path followed by the particle. Two examples are weight of the particle and elastic force of the spring. Potential Energy: It is the measure of the amount of work a conservative force will ...