Download r=2l L orbits!

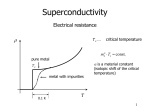
Spin Meissner effect in superconductors
and the origin of the Meissner effect
J.E. Hirsch, UCSD
Hvar, 2008
 Why the Meissner effect is not understood, and how it can be
understood
 Spin Meissner effect: spontaneous spin current in the ground
state of superconductors
 Charge expulsion, charge inhomogeneity in superconducting state
 Electrodynamic (London-like) equations for charge and spin
 Experiments
3 key pieces of the physics that BCS theory got right:
* Cooper pairs
* Energy gap
* Macroscopic quantum coherence
* Electron-phonon-induced attraction between electrons
(1) Key role of electron-hole asymmetry
(2) Key role of kinetic energy lowering as driving force
(3) Macroscopic charge inhomogeneity and internal E-field
(4) Key role of spin-orbit interaction
(5) Key role of mesoscopic orbits
(6) Spontaneous currents in the absence of applied fields
3 key pieces of the physics that BCS theory got right:
* Cooper pairs
* Energy gap
1988-2008
* Macroscopic quantum coherence
http://physics.ucsd.edu/~jorge/hole.html
* Electron-phonon-induced attraction between electrons
Meissner effect: expulsion of magnetic field from
interior of superconductor
cool
1933
The expulsion of magnetic flux from the interior of a superconducting metal when it is cooled in a magnetic
field to below the critical temperature, near absolute zero, at which the transition to superconductivity takes
place. It was discovered by Walther Meissner in 1933, when he measured the magnetic field surrounding two
adjacent long cylindrical single crystals of tin and observed that at ?452.97°F (3.72 K) the Earth's magnetic
field was expelled from their interior. This indicated that at the onset of superconductivity they became
perfect diamagnets. This discovery showed that the transition to superconductivity is reversible, and that the
laws of thermodynamics apply to it. The Meissner effect forms one of the cornerstones in the understanding
of superconductivity, and its led F. London and H. London to develop their phenomenological electrodynamics
of superconductivity.
The magnetic field is actually not completely expelled, but penetrates a very thin surface layer where currents
flow, screening the interior from the magnetic field.
lL=London penetration depth
two pathways to Meissner current
cool
B
normal
super
apply B
super
I
normal
EFaraday
cool
apply B
expel B
I
cool
I
same final state
Faraday electric field points in opposite directions
Meissner current I points in the same direction
Why the Meissner effect is a puzzle
Lower the temperature...
or lower slightly the applied H...
B
EFarad
I
Meissner
state
B=0
Current develops
'spontaneously' upon
cooling or lowering H
opposing EFarad
What is the 'force'pushing the electrons near the surface to
start moving all in the same direction, opposite to eEFarad ?
How is angular momentum conserved???
r=2lL orbits!
The key to the Meissner effect
B
I
cylinder
lL
R
vs
Angular momentum in Meissner current:
mev sR =angular momentum of 1 el
mevs (2lL )
bulk
2RlL hns =# of electrons in surface layer
R 2 hn s
(h=cylinder height, ns=superfluid density)
some very complicated math. . . . .

2lL
Le  (2RlL hns )  (mevsR)  (R hn s )  (mev s (2lL ))
2
Some simple relations:
Normal state:
Superconducting state:
Density of states at the
Fermi energy:
London penetration depth:
4 n se

2
lL
mec 2
1
3n 3nme
g(F ) 
 2 2
2F
kF
Magnetic susceptibility:
Magnetic susceptibility:
1 2
 Landau   B g(F )
3

1
 London  
4
1 n se 2
mec 2

4
2
2
4 me c 4 n se
1 e 2 3nme
 (
)( 2 2)
3 2mec
kF
ne 2
1 2


(k
F ) 
2
4me c
2


2
n se
2


(2
l
)

L
2
4mec
Larmor diamagnetism
B
v
Apply magnetic field B:
r
2


ner
v
 Larmor  n

B
4me c 2
1 B 2
1
 E  dl   c t  B  da  2rE   c t r
dv
er B 
er
 me
 eE  
 v  
B
dt
2c t
2mec
Orbital magnetic moment:

e
e
er
er
er er
e 2r 2
B
B

l
mevr  v    v  
2
2c
2c 2mec
4me c
2mec
2mec
2c

magnetic susceptibility per unit volume: n=electrons/unit vol
ne 2

ne 2 2
n se 2
1 2
2
 Larmor  n




(2
l
)


(k
)

2 r  
or
L
F
2
2
B
4me c
4mec
4me c
How the transition
occurs
n se 2
2
 Larmor  

r

2
4mec
B
r
Superconducting state:
2
Normal state:
n se
1
1 2
2
n se 2
1 2



(2
l
)




 Landau   B g(F )  
 (kF )  London
L
2
2
 4mec
4
4mec
3
orbit expansion:
-1
r=k
 F orbits
2lL
kF-1


r=2lL orbits
two pathways to Meissner current
apply B
super
expel B
normal
EFaraday
I
cool
I
same final state
The two pathways to the Meissner current
Apply magnetic field B:
Expand electron orbit in B:
Faraday's law pushes eB
v v
E
Lorentz force pushes eB
v
r
1
 E  dl   c t  B  da
dv
er B
 me
 eE  
dt
2c t
er

 v  
B
2mec

elL
 v  v  
B
me c
r
F
v
e
dv
F  v  B  Fr  me
c
dt
d
e
e d 2
(r  v )  
(r  v )B  
(r )B
dt
2mec
2mec dt
r=2lL
er
 v  
B
2mec
BCS:
 p  0 v  1 ( p  e A)
A  lL B
m
c
Why is there macroscopic phase coherence in superconductors?
r=kF-1 orbits
Normal state
Non-overlapping orbits
Relative phase doesn't matter
r=2lL orbits
Superconducting state
Highly overlapping orbits
Phase coherence necessary
to avoid collisions
A little help from a friend...
2
m
c
1
2
e
l:L 
, ns  3 ,
2
4 n se
a0
a0 
2
mee
2
==>
2


me c
1 c
2
2
l:L 

 a0 
a

2
2
2 0 

4e mee
4 e
2
2

137

A little help from a friend...
The speed of light must enter into the
superconducting
wave
function!
mc
1
l2:L 
2
e
4 n se
, ns 
2
a03
,
a0 
2
mee
2
==>
2


me c
1 c
2
2
l:L 

 a0 
a

2
2
2 0 

4e mee
4 e
2
2

137

So we learn from the Meissner effect that:
transition to superconductivity = expansion of electronic orbit from
r=kF-1 to r=2lL
What happens when there is no magnetic field?
Spin-orbit force deflects electron in expanding orbit!
Spin orbit scattering
(Goldberger&Watson)
spin-orbit
spin-orbit
scattering
center
scattering
center

v
v
p   
c


p

v
a moving magnetic moment is
equivalent to an electric dipole
So we learn from the Meissner effect that:
transition to superconductivity = expansion of electronic orbit from
r=kF-1 to r=2lL
What happens when there is no magnetic field?
Spin-orbit force deflects electron in expanding orbit!

p
v
v

E
p   
c
dL
   p  E
dt
d
v
1
me (r  v )  (  )  E  (E  v )
dt
c
c

v
d

 d 2
with E   r : me (r  v )  (r  v ) =
(r )
dt
c
2c dt
v

 E
 2
Er
B
 r  v  (r )
  v 
2mec
2c
2c
E
 v 
B
2mec
E  2r,
What's E?
 =| e | ns
r
8me l
2
L
E


v
2en sr
ensr e
 v 
B 
2mec
mec 2mec
v 

v
4 n se 2
1
; with
 2
2
mec
lL

For r=2lL

v 

==> L = me v r .

. . 
.
2
4me lL
!!!!!!!!
The two pathways to the Spin Meissner current
'Apply' electric field E:
Maxwell's law pushes 
E(t)
 B
v v
r
1 E
 B 
c t
Expand electron orbit in E:
Lorentz torque pushes 
 
v
r
v
v
  p  E  (  )  (2 | e | nsr )
c
dv
1
 me
 ( B)   ( B)   dL  m d (r  v )  e r  (v  B )
e
eff
dt
2
dt
dt
c
1 

( E )
Beff  2n s
2c t

er
nseB
1
n e
 v  
|  E |  s B r
 v  
Beff  
r
2mec
2mec
mec
mec
r=2lL


2
2n seB
n e
 v  v  
lL   2 s 2 lL  
==> L = mev r 
mec
me c
4me lL
2
Ground state of a superconductor
r=2lL orbits
r=2lL orbits
spin down electrons
spin up electrons
Currents in the interior cancel out, near the surface survive
==> there is a spontaneous spin current in the ground state of
superconductors!
There is a spontaneous spin current in the ground state of
superconductors, flowing within lL of the surface (JEH, EPL81, 67003 (2008))
v 0  
4mel L
 nˆ
no external
fields applied
For lL=400A, v072,395cm/s
e


2mec

v0
# of carriers in the spin current: ns
When a magnetic field is applied:
e
v  v 0 
l L B  nˆ
mec
B
n


v
The slowed-down spin component stops when
m ec
c

0
B
v 0 

~ Hc1 !
2
2
el L
4el L
4l L
 0  hc / 2 | e |
Summary of argument:
4 n se 2
1) 2 
lL
mec 2
(Ampere, Faraday, Newton, London)
2) Orbits have radius
2lL
1
(to explain origin of Meissner current)
e
3) Magnetic moment of electron is B 
2mec
4) Background positive charge density is | e | ns = - superfluid dens.

1)+2)+3)+4) ==>

L  /2
1)+2)+3)+4) ==> magnetic field that stops the spin current is Hc1

Therefore:
 Superconductivity is an
intrinsically relativistic effect
 Electron spin and associated magnetic moment plays a key role
 The wavefunction of a superconductor contains c=speed of light
Back
to: cooling
a superconductor
in the presence of a B-field:
A clue
from plasma
physics
What makes electrons move in the direction needed to create
all these currents when T is lowered from above to below Tc?
B
Vortex state
Meissner
state
B
I
I
B
I
Intermediate
state
A clue from plasma physics
www.mpia-hd.mpg.de/homes/fendt/Lehre/Lecture_OUT/lect_jets4.pdf
But if there is charge flow, it will result in charge inhomogeneity and
an electric field in the interior of superconductors.
 E  4
v
Meissner
state
B
Vortex state

FB
ve
I
e
FB  v  B
c
B
Intermediate
state
Electrons have to flow away from
the interior of the superconductor,
towards the surface and towards
the normal regions!
Le
B
I
Le
But if there is charge flow, it will result in charge inhomogeneity and
an electric field in the interior of superconductors.
 E  4
Can there be an electric field inside superconductors?
London says NO. First London equation (1934):
J ne

E
t
m
J  nev
2
free acceleration of electrons 
(n=density, v=speed, J=current)
If E = 0, J increases to infinity, unless Newton’s law is violated?
dv v
v2

   v  (  v ) !
dt t
2
dv
m
 eE
dt
2
ne
v ne
v
J
(E   )
E  ne(v  (  v )   ) 
 ne 
m
t
m
2
t
 J
can be zero even if E is non-zero!
t
2
2
New electrodynamic equations for superconductors (JEH, PRB69, 214515 (2004)
ne 2
c
1 4ne 2
1) J  
A
A ;

2
2
mc
4lL
lL
mc 2
1 A
J
ne 2 A ne 2
J ne 2
Note: E   


(E   ) , NOT

E
==>
t
mc t
m
c t
t
m
1 
0 ;
2)   A 
c t

(Lorenz gauge)
 J  
, continuity equation:  J 
c
4l2L

 A

1 

t
4l2L t
==> (r,t)  0  

 0 ==>
t
integrate in time, 1 integration constant 0 , ...

1
4l
2
L
[ (r,t)  0 (r)]
0 (r) 
0
 d r' | r  r'|
3
Electrodynamics
2
1

J
2
 J 2 J 2 2
lL
c t
2
1

B
2
 B 2 B 2 2
lL
c t
1
1
2
1

(E  E 0 )
 2 (E  E 0 )  2 (E  E 0 )  2
lL
c
t 2
 E 0  40
1
2
1

(  0 )
2

 (   0 )  2 (  0 )  2
lL
c
t 2
1
Relativistic form:
2
(A  A0 ) 
1
l
2
L
2
1

 2  2 2
c t
2
A  (A(r,t),i(r,t))
A0  (0,i0 (r ))
J  (J (r,t),ic(r,t))
(A  A0 )
or equivalently

J  J0  

c
(A  A0 ) 
2
4lL

J0  (0,ic0 )
Electrostatics:
 ( (r)  0 (r)) 
2
1
l
2
L
( (r)  0 (r))  2 ((r)  0 ) 
;
  (r)  4(r)   0 (r)  40
2
2
 2 (r)  0
 (E  E 0 ) 
2
1
l
2
L
1
l
2
L
((r)  0 )
(E  E 0 )
outside supercond.

+assume (r)
are continuous
 and its normal derivative

at surface
Solution for sphere of radius R:
R3
sinh( r / lL )
(r) =  0 (1 2
)
3lL R / lL cosh( R / lL )  sinh( R / lL )
No electric field outside sphere
lL
Sample size dependence of expelled charge (Q) and E-field
 < 0 = charge density near surface
0 > 0 = charge density in interior
sphere of radius R

0
Q ~ 0R3 ~ - R2 lL
lL
Electrostatic energy cost:
UE ~ Q2/R ~ ( R2 lL)2/R ~ ()2 R3 ~ (0)2 R5 ~ Volume~R3
==>  independent of R, 0 ~ 1/R
Electric field vs. r:
Em  4lL 
independent of R
E
Em
r
R1
R2
How much charge is expelled?
Emax

R
R
element
Tc(K)
Hc(G)
lL(A)
Extra elec- Em
trons/ion
(Volts/cm)
Al
1.14
105
500
1/17 mill
31,500
Sn
3.72
309
510
1/3.7 mill
92,700
Hg
4.15
412
410
1/2.5 mill
123,600
Pb
7.19
803
390
1/1 mill
240,900
Nb
9.50
1980
400
1/1.3 mill
308,400
Spin currents in superconductors (JEH, Phys. Rev. B 71, 184521 (2005))
Internal electric field (in the absence of applied B)
pointing out
 
k k
c c
E
carries a spin current
 


 c k
ck  ck
c k

Jch arg e
necessarily in the
presence of internal E-field
n
 (v  v )  0
no charge current ==> no B-field
2
n
Jspin  (v  v )  0
2
spin current without charge current!
Flows within a London penetration depth
of the surface
Speed of spin current carriers:
~ 100,000 cm/s
Number of spin current carriers:
=superfluid density
We now have 2 new pieces of physics of superconductors:
r=2lL orbits
charge expulsion
v 0 
4me lL


L  /2
0
lL


2lL
0  
 Em  4lL 
R
spin current
How are they related?


How much charge is expelled?
(JEH)
v 0 
~ Hc1
4me lL
 ==>
c
0
Em  

~ Hc1
2
2
4elL 4lL
c
v 0

  nse
3
16

e
l
c
 L
 J (r )  

c
2lL
2
1
E
n s ( me v2 0 )  m
2
8
(charge neutrality)
Emax
0
R
( (r )  0 )
J (r )  en sv (r )  
Em  4lL 
v 0 
4me lL

 
v0
c
8lL


 (E (r )  E 0 (r ))
2
1
B
2
n
(
m
v
)
(Recall s
e s )
2
8
n


Spin current electrodynamics (4d formulation)
Energetics
v  v  v0
v 0 
4me lL

1
 pair  2  me (v0 )2
2

Apply a magnetic
1
1
0
0 2
v  2v , v  0,  pair  me (2v )  4  me (v0 )
field:
2

==> condensation energy per particle:
2
1
c  me (v0 )2
2
energy lowering per particle in entering sc state:

2c
=
c
2c
c
+
Coulomb energycost + condensation energy
2
1
E
n s ( me v2 0 )  m
2
8
2
 2
1
1
2
m ev 0 
 ns B ~ 1.5eV ~ condensation
2
2
4 2m e (2l L )
2
energy of sc
Type I vs type II materials
x=distance between orbit centers
Type I: x> 2lL
Type II: x< 2lL
Phase difference:
e
p  mev  A,
c


p  
i
e
  me  v  dl  B
c
e
hc
  B  B   0
c
2e
h c
hc
0 
  
(2e) 2 e
What drives superconductivity?
1) Excess negative charge (CuO2)=, (MgB2)-, (FeAs)2) Almost full bands (hole conduction in normal state)
3) Kinetic energy lowering
(Kinetic energy is highest when band is almost full)
kF-1 is small
kF
too many electrons!
How is angular momentum conserved in the Meissner effect??
Electromagnetic field carries angular momentum!
B
Le
=-Le
But - is way too small to give enough Lfield
Spin-orbit interaction transfers counter-L to ions!
B
JEH, J. Phys.: Condens. Matter 20 (2008) 235233
Lfield
Lions
Experimental tests?
1) Detect spin current
* polarized light scattering (PRL100, 086603 (08)
* inelastic polarized neutron scattering
* photoemission
* Detect electric fields produced by spin current

v0
n
* Insert a 'spin current rectifier'
2) Detect internal electric field
* positrons, muons, neutrons
3) Response of superconductor to applied electric field
(Tao effect)
4) Detect change in plasmon dispersion relation in sc state
.....

IT IS A FALSIFIABLE THEORY!
To prove this theory wrong, find clear experimental
evidence for any of the following:
* A superconductor that has no spontaneous spin current near
the surface, with carrier density ns/2 and speed v  /4me lL
* A superconductor that has no outward-pointing electric field
in its interior
* A superconductor that expels magnetic fields without expelling
negative charge

* A superconductor that has no hole carriers in normal state
* A high Tc superconductor with no excess negative charge anywhere
* A superconductor with tunneling asymmetry of intrinsic
origin that has opposite sign to the one usually observed
* A superconductor with gap function that has no k dependence
* A superconductor not driven by kinetic energy lowering