* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 16 & 17 - Conroe High School
Anti-gravity wikipedia , lookup
Potential energy wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Field (physics) wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electromagnetism wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Lorentz force wikipedia , lookup
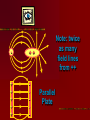
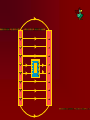
Electricity…the term brings to mind modern technologies Electricity Electric flow has a much deeper role in our life The forces between atoms and molecules that hold them together and form solids & liquids are electric forces Except for gravity, every force so far has been electric- All contact forces (push, pull, normal, elastic) are electric Gravity, strong nuclear and weak nuclear remain different. Electricity is tightly interwoven w/ magnetism 16-1 Electricity can be placed into 2 broad categories: static electricity and circuit electricity Opposite charges: attract Like charges: repel Two types of charges are positive negative The name of charges were given by…. BEN FRANKLIN When one thing gains a charge – the other thing loses a equal amount of charge Law of conservation of Electric Charge: “the net amount of electric charge produced in any process is zero” Electric charge in the atom + 0 - H holding an electric charge dry days yes, wet days no 0 +H IONS: + cosmic rays Conductors: metals, graphite, tap water Non- conductors: most everything else, pure water Semi- conductors: Si, Germanium, Carbon Insulators are often made of small atoms that hold their electrons tight(stingy) Conductors are generally atoms that are big with lots of electrons, e- are far away from nucleus Electroscope Detect presence of charge Charging by contact (conduction) Charging by induction Coulombs Law Charles Coulombs (frenchie) (17361806) developed an electrical law in the 1780’s Beautifully similar to Newton’s Universal Gravity- Coulomb’s experiments were also very similar to Cavendish’s gravity experiments Coulomb’s Law f = k Q1 Q2 r2 K = constant of proportionality Q = Charge f = force (attract or repel) r = distance between Q’s The coulomb is the SI unit of electric charge Electro statics are small and fall into the microcoloumb range (1x 10-6= 1uC) The charge on a single electron has been determined to be -1.602 x 10-19C (this is the smallest known charge) its called the elementary charge e = -1.602 x 10-19 The charge of a proton is +1.6 x 10-19C Direction of force depends on whether charges are… ++ -- +- -+ + + + - AP Test The AP test writes Coulomb’s law in terms of Eo not k Eo = Vacuum permittivity -12 2 2 = 8.85 x 10 C /Nm Electrostatic forces can be treated as vectors Fnet = f1 + f2 + f3 + … f1 f1 f1x f2 f1 f1y f2y f2 f2x f2 Electric Field Electric forces act over a distance The closer you get to a point charge, the stronger the field Force relates to distance by 1/r2 Test Charge +q fA A C +Q B fB fC Placed at 3 locations A, B, C Electric Field E units (N/C) E = F/q Definition of electric field- this defines the effect of the charge Electric Field due to a point charge… E = Kq Q/r2 q = In terms of Eo KQ r2 E = 1 / 4πEo Example problems Pg. 487- 489 Q/r2 Field Lines 1. 2. 3. The field lines indicate the direction of the electric field; the field points in the direction tangent to the field line at any point The Lines are drawn so that the magnitude of the electric field, E, is proportional to the number of lines crossing unit areas perpendicular to the lines. The closer the lines, the stronger the field Electric field lines start on positive charges and end on negative charge; the number starting or ending is proportional to the magnitude of the charge + - + + - ++ + + + + + - Note: twice as many field lines from ++ Parallel Plate Electric Field & Conductors The electric field inside a good conductor is zero in electrostatics Any net charge on a good conductor distributes itself on the surface A hollow metal box is placed in an electric field, the charge inside the box is zero + + + + + + + + + + + + - Conclusion: electrostatics is how photocopies work (pg. 487) also its what keeps our DNA together and unzips it for replication (pg. 493495) Class Work: Pg. 496 #’s 2, 5, 8, 9 Pg. 497 #’s 1, 3, 5,7 ,21, 23, 25 Chapter 17: Electric Potential, Electric Energy & Capacitance Energy is a conserved quantity, a very important aspect in nature + High + PE + + + b + + a - Low PE Think of (+) as falling towards (-) Work is done by electric field in moving the positive charge from b to a Electric Potential is the potential energy per unit charge Electric potential = Potential difference = Volts = Voltage Symbol: V V= PE/q UE = qV Vab = Va – Vb = -Wba/q Work is W, its negative because its done by electric field. Total energy is conserved PE to KE (for 2 points a & b) Fundamentally Voltage (Pd) is Joules/ Coulomb Energy/Charge J/C Think back to PE = mgh …it has similarities to V = PE/q O CLIFF h Which has more PE? + + Q + + + - 2Q - - In the voltage example 2Q has more PE b/c it has more charge. They have the same Height (voltage) Batteries & Generators Batteries and generators try to maintain a certain voltage. The actual amount of energy that flows depends on how much charge flows. If 5C of charge flowed through a head lamp in a car 5C x 12V = 60J of work would be done (light & heat) if for twice as long 120J = 10 x 12 Example pg. 505 a. b. c. ΔPE = qV =(-1.6 x 10-19C)(5000V) = -8.0 x 10-16J ΔKE = -ΔPE ½ mv2 - 0 = -qV V = √-2qV/m = 4.2 x 107m/s V = √-2qV/m = 9.8 x 105 m/s Energy doesn’t depend on mass but speed does OVERHEAD Fig. 17-3 Electron accelerator Relationship between Electric Potential & Electric Field Electric Potential is Scalar Electric field is Vector W = qV work done by electric field to move a charge Recall: f = qE W = fd therefore W = qEd (d = distance between plates) By Substitution… qV = qEd V = Ed E = V/d we see electric fields units are N/C as well as Volts/Meter Example Problem pg. 506 E = v/d 50V / .05m = 1000v/m Equipotential Lines Equipotential lines occur in 2-D Equipotential surfaces occur in 3-D Equipotential means that points along that line are the same potential. The Pd along that line or surface is zero Equipotential lines/ surfaces must be perpendicular to the electric field at any point. Overheads As long as you stay on a green line you never change Pd (voltage) If you walk on a contour line you never climb or descend. Going perpendicular to contour you change PEg rapidly Electron Volt a unit of energy An easy way to describe energy acquired by a particle carrying a charge equal to one electron, as a result of moving through 1 volt 1eV fundamental charge is the charge on an electron x 1 volt = qV 1.6 x 10-19C(1V) =1.6 x 10-19J 1eV = 1.6 x 10-19J This is not a SI unit for energy. Always convert to Joules using the above equivalency Energy Voltage due to Point Charges V = kQ/r = 1Q/4πEor This relates Voltage to Distance for a point charge Voltage is large when distance is small, true for both + and charges Example Problems: 17-3 Pg. 509 17-4 Pg. 510 Electric Dipole Two point charges of equal magnitude and opposite sign that are separated by a distance are an electric dipole B A 30 +Q Fig. 17-9 is an example 60 -Q Capacitance A condenser and capacitor are devices that store electric charge and are made of two conducting plates or sheets placed near each other but NOT touching Wide array of applications store charge for later use (cameras) energy back ups in computers if power fails Protect circuits by blocking surges Real small ones serve as memory in the RAM of computers the symbol for capacitors is (typically sheets/ plates) separated by an insulator and then rolled up into a small cylinder. When voltage is Applied (battery) the capacitor becomes charged. The amount of charge Q acquired by each plate is proportional to Voltage C is a constant of proportionality and it is the capacitance Q = CV C = Q/V (this has the units Farad F) Since surface area of sheet and distance of separation of plates matter, we also have a formula… C = Eo A / d Eo = 8.85 x 10-12 A = Surface Area d= Distance (m) Example 17-7 pg. 514 C = Eo A/ d -12 -2 • 8.85 x 10 (6 x 10 m) = 53 pF B. Q = CV • 53 x 10-12 (12V) = 6.4 x 10-10C A. Dielectrics Name given to the insulators between sheets in a capacitor. Purposes: Allow for higher charges to be applied without crossing gap. Dielectrics break down when the charge gets too high and lets charge leak slow. Allow sheets to be placed very close together By nature, dielectrics increase capacitance. This factor is K which is the dielectric constant. OVERHEAD Fig. 17-14 Storage of Electric Energy A capacitor stores electric energy. The stored energy is equal to the work done to charge it . The work done in charging a capacitor is to remove the charge from one plate and add it to the other plate The work done in charging is W = VΔq Energy stored in a capacitor is … Uc = Energy = ½ QV V=Voltage Q=Charge on plate Uc=Energy We can also write Uc = ½ QV = ½ CV2 = ½ Q2/C Example problem 17-9 pg. 517 U = ½ CV2 = ½ (150 x 10-6f)(200V)2 = 3J If the energy is released in 1/1000 sec Power output is 3000 W