Download Chapter 16 & 17 - Conroe High School

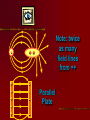
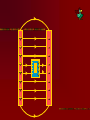
Electricity…the term
brings to mind modern
technologies
Electricity




Electric flow has a much deeper role in our
life
The forces between atoms and molecules
that hold them together and form solids &
liquids are electric forces
Except for gravity, every force so far has
been electric- All contact forces (push, pull,
normal, elastic) are electric
Gravity, strong nuclear and weak nuclear
remain different. Electricity is tightly
interwoven w/ magnetism
16-1
Electricity can be placed into 2
broad categories: static electricity
and circuit electricity
 Opposite charges: attract
 Like charges: repel
 Two types of charges are
 positive
 negative

The name of charges were
given by….
BEN FRANKLIN
 When
one thing gains a charge
– the other thing loses a equal
amount of charge
 Law of conservation of Electric
Charge: “the net amount of
electric charge produced in any
process is zero”
Electric charge in the atom
+
0
-
H
holding an electric charge
dry days yes, wet days no
0
+H
IONS:
+
cosmic rays
Conductors: metals, graphite, tap water
 Non- conductors: most everything else,
pure water
 Semi- conductors: Si, Germanium,
Carbon
 Insulators are often made of small atoms
that hold their electrons tight(stingy)
 Conductors are generally atoms that are
big with lots of electrons, e- are far away
from nucleus

Electroscope
 Detect
presence of charge
 Charging by contact
(conduction)
 Charging by induction
Coulombs Law
Charles Coulombs (frenchie) (17361806) developed an electrical law in the
1780’s
 Beautifully similar to Newton’s
Universal Gravity- Coulomb’s
experiments were also very similar to
Cavendish’s gravity experiments

Coulomb’s Law
f = k Q1 Q2
r2
K = constant of proportionality
Q = Charge
f = force (attract or repel)
r = distance between Q’s
The coulomb is the SI unit of electric
charge
 Electro statics are small and fall into
the microcoloumb range (1x 10-6= 1uC)
 The charge on a single electron has
been determined to be -1.602 x 10-19C
(this is the smallest known charge) its
called the elementary charge

e = -1.602 x 10-19
 The charge of a proton is +1.6 x 10-19C
 Direction of force depends on whether
charges are…

++
--
+-
-+
+
+
+
-
AP Test
 The
AP test writes
Coulomb’s law in terms of
Eo not k
 Eo = Vacuum permittivity
-12
2
2
= 8.85 x 10 C /Nm
Electrostatic forces can be
treated as vectors
Fnet = f1 + f2 + f3 + …
f1
f1
f1x
f2
f1
f1y
f2y
f2
f2x
f2
Electric Field
 Electric
forces act over a
distance
 The
closer you get to a point
charge, the stronger the field
 Force relates to distance by 1/r2
Test Charge +q
fA
A
C
+Q
B
fB
fC
Placed at 3
locations
A, B, C
Electric Field E units (N/C)
E = F/q
 Definition of electric field- this defines
the effect of the charge
 Electric Field due to a point charge…

E = Kq Q/r2
q
=
In terms of Eo
KQ
r2
E = 1 / 4πEo
Example problems
Pg. 487- 489
Q/r2
Field Lines
1.
2.
3.
The field lines indicate the direction of the
electric field; the field points in the direction
tangent to the field line at any point
The Lines are drawn so that the magnitude of
the electric field, E, is proportional to the
number of lines crossing unit areas
perpendicular to the lines. The closer the lines,
the stronger the field
Electric field lines start on positive charges and
end on negative charge; the number starting or
ending is proportional to the magnitude of the
charge
+
-
+
+
-
++
+
+
+
+
+
-
Note: twice
as many
field lines
from ++
Parallel
Plate
Electric Field & Conductors
 The
electric field inside a good
conductor is zero in electrostatics
 Any net charge on a good
conductor distributes itself on the
surface
 A hollow metal box is placed in an
electric field, the charge inside the
box is zero
+
+
+
+
+
+
+
+
+
+
+
+
-
 Conclusion:
electrostatics is how
photocopies work (pg. 487) also its
what keeps our DNA together and
unzips it for replication (pg. 493495)
 Class Work:
 Pg. 496
#’s 2, 5, 8, 9
 Pg. 497
#’s 1, 3, 5,7 ,21, 23, 25
Chapter 17:
Electric Potential, Electric Energy &
Capacitance
 Energy
is a conserved quantity, a
very important aspect in nature
+
High +
PE + +
+ b
+
+ a -
Low
PE
Think of (+) as
falling towards (-)
 Work
is done by electric field in
moving the positive charge from b
to a
 Electric Potential is the potential
energy per unit charge
 Electric potential = Potential
difference = Volts = Voltage
Symbol: V
V= PE/q
UE = qV
Vab = Va – Vb = -Wba/q
 Work is W, its negative because its
done by electric field. Total energy is
conserved PE to KE (for 2 points a & b)
 Fundamentally Voltage (Pd) is
 Joules/ Coulomb
 Energy/Charge
 J/C
 Think
back to PE = mgh …it
has similarities to V = PE/q
O
CLIFF
h
Which
has more
PE?
+
+
Q
+
+
+
-
2Q
-
-
In the voltage
example 2Q has
more PE b/c it has
more charge. They
have the same
Height (voltage)
Batteries & Generators
Batteries and generators try to
maintain a certain voltage.
 The actual amount of energy that
flows depends on how much charge
flows. If 5C of charge flowed through
a head lamp in a car 5C x 12V = 60J of
work would be done (light & heat) if
for twice as long 120J = 10 x 12

Example pg. 505
a.
b.
c.
ΔPE = qV
=(-1.6 x 10-19C)(5000V)
= -8.0 x 10-16J
ΔKE = -ΔPE
½ mv2 - 0 = -qV
V = √-2qV/m = 4.2 x 107m/s
V = √-2qV/m = 9.8 x 105 m/s
Energy doesn’t depend on mass but
speed does
OVERHEAD
Fig. 17-3 Electron
accelerator
Relationship between Electric
Potential & Electric Field
 Electric
Potential is Scalar
 Electric field is Vector
 W = qV work done by electric
field to move a charge
 Recall: f = qE W = fd
 therefore
W = qEd
(d = distance between plates)
By Substitution…
 qV
= qEd
 V = Ed
 E = V/d
 we see electric fields units
are N/C as well as
Volts/Meter
Example Problem pg. 506
E = v/d
50V / .05m
= 1000v/m
Equipotential Lines
Equipotential lines occur in 2-D
 Equipotential surfaces occur in 3-D
 Equipotential means that points
along that line are the same
potential. The Pd along that line or
surface is zero
 Equipotential lines/ surfaces must
be perpendicular to the electric field
at any point.

Overheads

As long as you stay on a green line
you never change Pd (voltage)

If you walk on a contour line you
never climb or descend. Going
perpendicular to contour you
change PEg rapidly
Electron Volt
a
unit of energy
 An easy way to describe energy
acquired by a particle carrying a
charge equal to one electron, as
a result of moving through 1 volt
 1eV fundamental charge is the
charge on an electron x 1 volt
= qV 1.6 x 10-19C(1V)
=1.6 x 10-19J
1eV = 1.6 x 10-19J
This is not a SI unit for energy.
Always convert to Joules using
the above equivalency
 Energy
Voltage due to Point Charges
V = kQ/r = 1Q/4πEor
This relates Voltage to Distance
for a point charge
Voltage is large when distance is
small, true for both + and charges
Example Problems:
17-3 Pg. 509
17-4 Pg. 510
Electric Dipole
Two point charges of equal magnitude
and opposite sign that are separated
by a distance are an electric dipole
B
A
30
+Q
Fig. 17-9 is an example
60
-Q
Capacitance
A condenser and capacitor are
devices that store electric
charge and are made of two
conducting plates or sheets
placed near each other but
NOT touching
Wide array of applications





store charge for later use (cameras)
energy back ups in computers if power fails
Protect circuits by blocking surges
Real small ones serve as memory in the
RAM of computers
the symbol for capacitors is
(typically sheets/
plates) separated by an insulator and then rolled
up into a small cylinder. When voltage is Applied
(battery) the capacitor becomes charged.

The amount of charge Q acquired by each
plate is proportional to Voltage


C is a constant of proportionality and it is
the capacitance


Q = CV
C = Q/V (this has the units Farad F)
Since surface area of sheet and distance of
separation of plates matter, we also have a
formula…


C = Eo A / d
Eo = 8.85 x 10-12 A = Surface Area d= Distance
(m)
Example 17-7 pg. 514
C = Eo A/ d
-12
-2
• 8.85 x 10
(6 x 10 m)
= 53 pF
B. Q = CV
• 53 x 10-12 (12V)
= 6.4 x 10-10C
A.
Dielectrics


Name given to the insulators between
sheets in a capacitor.
Purposes:
 Allow for higher charges to be applied
without crossing gap.
 Dielectrics break down when the charge
gets too high and lets charge leak slow.
 Allow sheets to be placed very close
together
 By
nature, dielectrics
increase capacitance. This
factor is K which is the
dielectric constant.
OVERHEAD
Fig. 17-14
Storage of Electric Energy
A
capacitor stores electric energy.
The stored energy is equal to the
work done to charge it . The work
done in charging a capacitor is to
remove the charge from one plate
and add it to the other plate
 The work done in charging is
W = VΔq
 Energy
stored in a capacitor is …
 Uc = Energy = ½ QV
V=Voltage Q=Charge on plate
Uc=Energy
 We can also write
 Uc = ½ QV = ½ CV2 = ½ Q2/C
Example problem 17-9 pg. 517
U = ½ CV2
= ½ (150 x 10-6f)(200V)2
= 3J
If the energy is released in
1/1000 sec
Power output is 3000 W