Download document 8624133

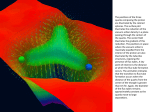
Color, Gluons Gluons are the exchange par1cles which couple to the color charge . They carry simultaneously color and an1color. red
antigreen
antiblue
blue
green
antired
What is the total number of gluons? According to SU3, 3x3 color combina1ons form a singlet and an octet. The octet states form a basis from which all other color states can be constructed. The way in which these eight states are constructed from colors and an1colors is a maEer of conven1on. One possible choice is: RG , RB , GB , GR , BR , BG ,
(
)
(
1 / 2 RR − GG , 1 / 6 RR + GG − 2 BB
)
The color singlet: 1 / 3 RR + GG + BB
is invariant with respect of a re-­‐defini1on of the color names (rota1on in color space). Therefore, it has no effect in color space and cannot be exchanged between color charges. (
)
emission of a gluon
by a quark
q→q+g
splitting of a gluon
into a quark-antiquark pair
g→q+q
self-coupling of gluons
g→ g+g
g+g→ g+g
hEp://www.par1clezoo.net/shop.html hEp://commons.wikimedia.org/wiki/File:Neutron_QCD_Anima1on.gif meson
π+
baryon
!
#
#
="
#
#
$
uR d R
uB dB
g
b
uG dG
Meson can exist in three different color combina1ons. The actual pion is a mixture of these color states. By exchange of gluons, the color combina1on con1nuously changes. _
bg
_
gb
g
r
_
rg
_
g
_
b
_
g
_
r
QCD vacuum
In QED vacuum polariza1on effects are extremely weak, because the electron has a small charge and a non-­‐zero rest mass. On the other hand, the QCD gluons are massless, and their strong interac1on is not damped by a small parameter. As a result, the QCD vacuum polariza1on effect is extremely strong, and the empty space is not empty at all -­‐ it must contain a soup of spontaneously appearing, interac1ng, and disappearing gluons. Moreover, in the soup there also must be pairs of virtual quark-­‐an1quark pairs that are also color-­‐charged, and emit and absorb more virtual gluons. It turns out that the QCD ground state of an “empty” space is extremely complicated. At present, we do not have any glimpse of a possibility to find the vacuum wave func1on analy1cally. Some ideas of what happens are provided by the QCD lamce calcula1ons, in which the gluon and quark fields are discre1zed on a four-­‐dimensional lamce of space-­‐1me points, and the differen1al field equa1ons are transformed into finite-­‐difference equa1ons solvable on a computer. hEp://www.physics.adelaide.edu.au/theory/staff/leinweber/VisualQCD/Nobel/index.html The typical four-­‐dimensional structure of gluon-­‐field configura1ons averaged over in describing the vacuum proper1es of QCD. The volume of the box is 2.4 by 2.4 by 3.6 fm, big enough to hold a couple of protons. •  Three quarks indicated by red, green and blue spheres (lower leb) are localized by the gluon field. •  A quark-­‐an1quark pair created from the gluon field is illustrated by the green-­‐an1green (magenta) quark pair on the right. These quark pairs give rise to a meson cloud around the proton. hEp://www.physics.adelaide.edu.au/theory/staff/leinweber/VisualQCD/Nobel/index.html The posi1ons of the three quarks composing the proton are illustrated by the colored spheres. The surface plot illustrates the reduc1on of the vacuum ac1on density in a plane passing through the centers of the quarks. The vector field illustrates the gradient of this reduc1on. The posi1ons in space where the vacuum ac1on is maximally expelled from the interior of the proton are also illustrated by the tube-­‐like structures, exposing the presence of flux tubes. A key point of interest is the distance at which the flux-­‐tube forma1on occurs. The anima1on indicates that the transi1on to flux-­‐tube forma1on occurs when the distance of the quarks from the center of the triangle is greater than 0.5 fm. Again, the diameter of the flux tubes remains approximately constant as the quarks move to large separa1ons. Quarks In 1968, deep inelas5c sca7ering experiments at the Stanford Linear Accelerator Center showed that the proton contained much smaller, point-­‐like objects and was therefore not an elementary par1cle A
t
tz
u (up)
1
1
2
−1
2
d (down)
1
2
+1
2
s (strange)
1
c (charm)
1
b (bottom)
1
t (top)
1
Flavor
3
3
3
3
3
3
1
Mc 2 (GeV)
S
C
B
T
Q(e)
0
0
0
0
+2
3
0.002 − 0.003
0
0
0
0
−1
3
0.004 − 0.006
0
0
−1 0
0
0
−1
3
0.08 − 0.13
0
0
0
1
0
0
+2
3
1.2 −1.3
0
0
0
0 −1 0
−1
3
0
0
0
0
+2
3
0
1
4.1− 4.3
• The least massive are u- and d-quarks (hence the lightest baryons and
mesons are made exclusively of these two quarks)
• Each quark has baryon number A=1/3.
• Strange quark carries a quantum number called strangeness S.
Strange particles (such as kaons) carry this quark
• Six antiquarks complement the list
• Quarks are all fermions; they carry half-integer spins
τ+ u =
• d- and u-quarks form an isospin doublet
• Strong interactions conserve the total number of each type of quarks.
However, quarks can be transformed from one flavor to another
through weak interactions (CKM matrix!).
173±1
d
τ− d = u
Nucl. Phys. A750, 84 (2005)
1000000
QCD mass
Higgs mass
Mass (MeV)
100000
10000
1000
100
10
1
u
d
s
c
b
t
GeV
HOW does the rest of the proton mass arise?
HOW does the rest of the proton spin (magnetic moment,…), arise?
Mass from nothing
Dyson-Schwinger and Lattice QCD
It is known that the dynamical chiral symmetry breaking; namely, the generation of mass from nothing, does
take place in QCD. It arises primarily because a dense cloud of gluons comes to clothe a low- momentum
quark. The vast bulk of the constituent-mass of a light quark is contained in a cloud of gluons, which are
dragged along by the quark as it propagates. In this way, a quark that appears to be absolutely massless at
high energies acquires a large constituent mass at low energies.
Chiral symmetry
For massless quarks, QCD Lagrangian preserves helicity. Indeed, since a massless quark travels at the speed of light, the handedness or chirality of the quark is independent of any Lorentz frame from which the observa1on is made.
LQCD = LQCD (ψ L ) + LQCD (ψ R )
the QCD interaction does not couple the
left and right-handed quarks
The mass term explicitly breaks the chiral symmetry as:
mqψ qψ q = mqψ qLψ qR + mqψ qRψ qL
The main origin of the chiral symmetry breaking, however, may be described in
terms of the fermion condensate (vacuum condensate of bilinear expressions
involving the quarks in the QCD vacuum) formed through nonperturbative action
of QCD gluons.
Spontaneous symmetry breaking due to the strong low-energy QCD dynamics,
which rearranges the QCD vacuum:
3
ψ qLψ qR ∝ Λ QCD
≠0
Spontaneous Symmetry Breaking (SSB) I SSB is associated with the observance of massless excita8ons called Goldstone bosons. (In prac8ce, they may be merely unusually light rather than massless if there is also explicit symmetry breaking; this is the case for pions.) The case of the ferromagnet with spins is easiest to visualize. Imagine a laGce of spins at high temperatures, which fluctuate in direc8on such that the net magne8za8on is always zero. The Hamiltonian for this system respects rota8onal symmetry: there is no preferred direc8on. However, the lowest energy configura8on would have all spins pointed in the same direc8on. But what direc8on? All possible choices are degenerate in energy. If we cool the system from a high temperature, below a cri8cal temperature, one direc8on will be picked out. This is spontaneous symmetry breaking: the vacuum (ground state) of the system breaks the symmetry of the Hamiltonian, at least in part. In this case, there is s8ll rota8onal symmetry about the axis of the direc8on picked out. Now think of the lowest energy excita8ons. If we imagine a long wavelength quan8zed spin wave, in which the direc8on of the spin changes very slowly, then within the wavelength, the energy of the excita8on is near zero, because they are simply spins poin8ng in another direc8on. Spontaneous Symmetry Breaking (SSB) II The more formal way to think of this is in terms of an effec8ve poten8al, e.g., for a scalar field, which tells us about possible ground states for a field theory. The Mexican hat poten8al shown above manifests SSB. All choices in the boPom of the valley have the same energy. But one is picked out in the vacuum -­‐-­‐-­‐ this is spontaneously symmetry breaking. But then low-­‐lying excita8ons in the original symmetry direc8on cost very liPle. Therefore SSB leads to massless Goldstone bosons. Light pions are the Goldstone bosons of chiral symmetry breaking in QCD. Low-lying Hadron Spectrum
Dürr, Fodor, Lippert et al., BMW Collaboration
Science 322, 1224 (2008)
More than 99% of the mass of the visible universe is made up of protons and neutrons. Both particles are much
heavier than their quark and gluon constituents, and the Standard Model of particle physics should explain this
difference. We present a full ab initio calculation of the masses of protons, neutrons, and other light hadrons, using
lattice quantum chromodynamics. Pion masses down to 190 mega–electron volts are used to extrapolate to the
physical point, with lattice sizes of approximately four times the inverse pion mass. Three lattice spacings are used
for a continuum extrapolation. Our results completely agree with experimental observations and represent a
quantitative confirmation of this aspect of the Standard Model with fully controlled uncertainties
The spin structure of the nucleon
Rev. Mod. Phys. 85, 655 (2013)
How do the proton’s various constituents contribute to its overall spin? As illustrated by the diagram, the
quarks, antiquarks, and gluons are all believed to have their own intrinsic spins, and these must contribute. But
so also must the relative orbital motions of the quarks and gluons inside the proton. The first measurements of
the proton’s spin substructure have been made recently, employing the technique of deep inelastic scattering
with spin-polarized beams bombarding spin-polarized targets. By combining these measurements with
constraints from other data, one can infer the fraction of the proton’s spin carried by the intrinsic spin of quarks
(and antiquarks) of different flavors. The results of experiments performed at CERN, SLAC, and DESY,
summarized in the graph, point to an unexpected outcome: all the quarks and antiquarks together account for
no more than one-third of the total spin. More direct probes of the spin alignment of different flavors of
quarks, separation of the contributions from quarks and antiquarks, and extraction of information on the gluon
spin contributions are goals of ongoing and planned second-generation experiments.
http://physicsworld.com/cws/article/news/2014/jul/11/gluons-get-in-on-proton-spin
http://www.scientificamerican.com/article/proton-spin-mystery-gains-a-new-clue1/
4
Where is the glue? Search for exotic particle
negative parity
positive parity
exotics
2.5
?
2.0
1.5
1.0
isoscalar
0.5
Phys. Rev. D 84, 074023 (2011)
isovector
YM glueball
http://www.gluex.org
• 
• 
• 
• 
FIG. 1. A compilation of recent p
lattice QCD computations for both the isoscalar and isovector light mesons from Ref. [1],
¯ ⌘ (|uūi + |ddi)/
¯
including ``¯ |``i
2 and ss̄ mixing angles (indicated in degrees). The dynamical computation is carried out
with two flavors of quarks, light (`) and strange (s). The s quark mass parameter is tuned to match physical ss̄ masses, while
the light quark mass parameters are heavier, giving a pion mass of 396 MeV. The black brackets with upward ellipses represent
Non-quark
model
mesons
include
exotic
whichadditional
have states. The dotted boxes indicate states
regions of the
spectrum
where present
techniques
make mesons,
it difficult to extract
that are interpreted
the lightest
hybridfor
multiplet
– the extraction
of clear model;
0 + states in this region is difficult in practice.
quantum
numbersas not
possible
mesons
in the quark
glueballs or gluonium, which have no valence quarks at all;
tetraquarks, which have two valence quark-antiquark pairs;
hybrid mesons, which contain a valence quark-antiquark pair and
one or more gluons.
http://www.symmetrymagazine.org/article/september-2006/the-rise-and-fall-of-the-pentaquark