Download E + - IPAM

Computational Complexity of
Quantum Systems
Sandy Irani
Computer Science Department
University of California, Irvine
Visiting Institute for Quantum
Information, Caltech
Complexity of Quantum Systems
• Can the evolution of a quantum system be
simulated efficiently on a classical
computer?
• How hard is to approximate interesting
properties of a quantum system (for
example, ground state energy)?
One-dimensional Quantum Systems
• Density Matrix Renormalization Group (DMRG)
method has been successful at computing the ground
state and time evolution of a quantum system.
[White][Vidal][Verstraete and Cirac][Schollwock]
• 1-D quantum systems can perform universal quantum
computation with nearest neighbor interactions.
• 1-D quantum cellular automaton can perform universal
quantum computation.
[Watrous][Shepherd, Franz and Werner]
Complexity of Quantum Systems
• Adiabatic Evolution [Farhi, Goldstone, Gutman and Sipser]
– Can a quantum computation be embedded in the ground
state of a quantum system?
• QMA-completeness
– Can we prove that computing properties of a quantum
system are hard with respect to a complexity class?
• Entanglement
– Bounded entanglement accounts for the success of some
numerical methods. Can we formally bound the
entanglement for classes of quantum systems?
Complexity Classes
• Resources required to solve a problem grow
with the size of the input
– Example: time required to sort n numbers will
grow with n.
– Question: How does the time grow with n?
• How to measure time complexity?
– Time on a particular platform (language, compiler,
processor, etc.)
– Number of instructions executed
– Steps on a Turing Machine
– Gates in a circuit
Polynomial Time
• Class P:
– The set of problems that can be solved on
a “reasonable” (classical) model of
computation [Turing Machine, PC, circuit,
etc.] such that the complexity is bounded
by a polynomial as the size of the input
increases.
• (e.g. sorting n numbers in time n log n )
• For simplicity, we often refer to decision
problems (yes, no answers).
• Decision problem <-> Language
– – set of “yes” instances
The Class NP
• A language L is in the class NP, if there is a
deterministic polynomial time algorithm V
and polynomial p such that
– If x is in L, there exists y (witness, certificate)
such that |y|<p(|x|) and
V(x,y)=“accept”
– If x is not in L, for all y such that |y|<p (|x|)
V(x,y)=“reject”
Quantum Complexity Classes
NP
P
Boolean 3-Satisfiability Problem
• Input: boolean formula expressed as the disjunction
of clauses each of which contains three literals:
x2  x7  x11   x3  x6  x13     x17  x7  x6 
Clause 1
Clause 2
Clause m
• Output: “Yes” or “No” depending on whether there is
a truth assignment of the variables which causes
each clause to evaluate to true.
Complete Problems
• Hardest problems in a complexity class.
• Any problem in the class can be reduced to a
complete problem.
Generic
Problem
In NP
3-SAT
“Yes”
instances
Satisfiable
Formulae
“No”
Unsatisfiable
Formulae
instances
Original Proof that 3SAT is
NP-complete
Polynomial time verifier V
(circuit, Turing machine,
Random-Access-Machine…)
For a problem in NP
+
Problem input
There is a witness
that causes V to
accept
3-SAT Formula
IFF
There is a satisfying
assignment for the
3-SAT formula
Encode the dynamic process of a computation (verifier) into a
static boolean formula.
[Cook, Levin 1971]
Quantum Complexity Classes
NP
P
NP-complete
Problems
What about quantum complexity?
• A problem P is in BPP if there exists a
universal family of polynomial size circuits
Cn (n denotes the length of the input) such
that for each x of length n:
r
Cn
0/1
x
• If P(x)=“yes”, Prob[Cn(x)=1] > 2/3
• If P(x)=“no”, Prob[Cn(x)=0] > 2/3
What about quantum complexity?
• A problem P is in BPP if there exists a
universal family of polynomial size circuits
Cn (n denotes the length of the input) such
that for each x of length n:
r
Cn
0/1
x
• If P(x)=“yes”, Prob[Cn(x)=1] > 2/3
• If P(x)=“no”, Prob[Cn(x)=0] > 2/3
1-1/e
1-1/e
Quantum Complexity Classes
NP
P
BPP
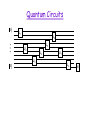
Quantum Circuits
0

U1
U6
U5
U2
U4
U3
0
U7
U8
M
Universal Set of Gates
• Two qubit gates suffice:
– Any arbitrary unitary operation can be
expressed exactly as a product of
unitary operations, each of which acts
non-trivially on only two qubits.
• There is a finite universal set of
gates:
– There exists a finite set of gates such
that any unitary operation can be
approximated to arbitrary accuracy by a
quantum circuit involving only those
gates.
BQP
• A problem L is in BQP if there exists a universal
family of polynomial size quantum circuits Cn (n
denotes the length of the input) such that for each
x of length n:
Answer bit
0
Cn
x
• If P(x)=“yes”, Prob[Cn(x)=1] > 2/3
• If P(x)=“no”, Prob[Cn(x)=0] > 2/3
[Deutsch][Yao][Bernstein,Vazirani]
Quantum Complexity Classes
NP
P
BPP
BQP
The Class Merlin-Arthur
• A language L is in the class MA, if there is a
randomized polynomial time algorithm C and
polynomial p such that
– If x is in L, there exists y such that |y|<p(|x|)
and
Prob[C(x,y)=1] > 2/3
– If x is not in L, for all y such that |y|<p (|x|)
Prob[C(x,y)=0] > 2/3
The Class Merlin-Arthur
• A language L is in the class MA, if there is a
randomized polynomial time algorithm C and
polynomial p such that
– If x is in L, there exists y such that |y|<p(|x|)
and
Prob[C(x,y)=1] > 2/3 1-1/e
– If x is not in L, for all y such that |y|<p (|x|)
Prob[C(x,y)=0] > 2/3 1-1/e
Quantum Complexity Classes
MA
NP
P
BPP
BQP
QMA
• A language L is in the class QMA, if there is a
polynomial sized quantum circuit C and polynomial
p such that
– If x is in L, there exists  , a quantum state on at most
p(|x|) qubits
Prob[C(x,  )=1] > 2/3
– If x is not in L, for all  such that
state on p(|x|) qubits,
Prob[C(x,  )=0] > 2/3
[Kitaev]

is a quantum
QMA
• A language L is in the class QMA, if there is a
polynomial sized quantum circuit C and polynomial
p such that
– If x is in L, there exists  , a quantum state on at most
p(|x|) qubits
Prob[C(x,  )=1] > 2/3 1-1/e
– If x is not in L, for all  such that
state on p(|x|) qubits,
Prob[C(x,  )=0] > 2/3 1-1/e
[Kitaev]

is a quantum
Quantum Complexity Classes
PSPACE
QMA
MA
NP
P
BPP
BQP
Quantum Complexity Classes
Where does
the problem of computing
ground energy fit into
this picture?
PSPACE
QMA
MA
NP
P
BPP
BQP
Quantum Complexity Classes
Where does
the problem of computing
ground energy fit into
this picture?
PSPACE
QMA-complete
QMA
MA
NP
P
BPP
BQP
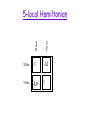
Restrictions on the Hamiltonian
• A Hamiltonian H is a d-state k-local
Hamiltonian if it acts on a system of d-state
particles and can be written as a sum of
terms, each of which acts non-trivially on a
set of k particles.
• H is an r-dimensional d-state Hamiltonian if
it is a d-state 2-local Hamiltonian and each
term interacts non-trivially on only nearest
neighbor particles arranged in an rdimensional grid.
Local Hamiltonian Problem
• d-STATE k-LOCAL HAMILTONIAN
Let H be a d-state k-local Hamiltonian. Then
(H, E0,D) is in d-STATE k-LOCAL HAMILTONIAN
if the ground state E0 of H is at most E. The
system must satisfy the promise that either E0 is
at most E or at least E + D.
D will be 1/poly in the size of the system
Theorem: 2-State 5-Local HAMILTONIAN is
QMA-complete [Kitaev]
5-local Hamiltonian
• Given a quantum verifier C(  0 )
• Find 5-local Hamiltonian H such that
– If there is a  such that C accepts with high
probability, then the ground state of H has
energy at most E.
– If for every  probability C accepts is low,
then every eigenstate of H has energy at least
E+D.
Classical/Qauntum
• Turing machine computation
(Verfier)
• Set of variables with
possible settings
• Instance of k-Sat (set of
constraints on the variables)
• Variable settings
• Cost of the assignment
• Quantum circuit (Verfier)
• Set of particles each with a
finite set of states
• Hamiltonian H – sum of terms
with energy constraints
• Quantum state
• Energy of the state
5-local Hamiltonian
•
•
•
•
•
Suppose we have a quantum verifier circuit that is composed of T
gates operating on n qubits. (Both witness and ancillary qubits).
Will have a system composed of n computation qubits and T+1 clock
quibits.
Let  denote a possible quantum witness.
Let  t denote the state of the n quibits after the first t gates have
been applied.  0   0...0
The constraints of the 5-local Hamiltonian will ensure that any low
energy state must have the form:
T
1
t 1 T t

1
0

t
T  1 t 0
•
Then one final constraint that places an energy penalty on a state for
which the outcome of the verifier is 0.
2-quibit system
Encode constraints onto an eigenstate that
corresponds to an eigenvector of 0.
• Forbid
00 01 10 11
00
00 1
01 0
10 0

11 0
0
0
0
0
0
0
0
0
0
0
0

0
2-quibit system
• Enforce that amplitude of 01 is the
same as the amplitude of 10 .
00
01 10 11
00 0
0
0
01 0 1 / 2  1 / 2
10 0  1 / 2 1 / 2

11 0
0
0
0
0
0

0
• Any 0 eigenvalue will be of form
    
2-quibit system
• Any 0 eigenstate of this Hamiltonian
00
01 10 11
00 1
0
0
01 0 1 / 2  1 / 2
10 0  1 / 2 1 / 2

11 0
0
0
0
0
0

1
• Must be
1
1

01 
10   0
2
2

1
2
1
2

0

5-local Hamiltonian
• Suppose that gate t operates on qubits 1 and 2 with unitary
operator U
• Want a 5-qubit terms that ensures for every state of the form:
x1 , x2 , x3 ,..., xn 111...100...0
t
• The following state has equal amplitude:
U x1 , x2 x3 ,..., xn 111...110...0
t+1
5-local Hamiltonian
• Suppose that gate t operates on qubits 1 and 2 with unitary
operator U
• Want a 5-qubit terms that ensures for every state of the form:
x1 , x2 , x3 ,..., xn 111...100...0
• The following state has equal amplitude:
U x1 , x2 x3 ,..., xn 111...110...0
100xx
I
110xx
-U+
110xx
100xx
5-local Hamiltonian
-U
I
Dynamic vs. Static Qauntum
Computation
• Quantum circuit: dynamic
– Different gates applied at different points in
time.
– Qubits physically situated on a line not limiting.
• Ground state of a Hamiltonian: static
– Ground state must satisfy constraints imposed
by Hamiltonian.
– Complexity of ground state may be affected by
• Locations of particles
• Types of terms allowed in Hamiltonian
QMA-Complete Problems
• 5-Local Hamiltonian is QMA-complete
[Kitaev]
QMA-Complete Problems
• 5-Local Hamiltonian is QMA-complete
[Kitaev]
• 2-Local Hamiltonian is QMA-complete
[Kempe, Kitaev,Regev]
QMA-Complete Problems
• 5-Local Hamiltonian is QMA-complete
[Kitaev]
• 2-Local Hamiltonian is QMA-complete
[Kempe, Kitaev,Regev]
• 2-Dim 2-State Hamiltonian is QMAcomplete [Oliveira, Terhal]
QMA-Complete Problems
• 5-Local Hamiltonian is QMA-complete
[Kitaev]
• 2-Local Hamiltonian is QMA-complete
[Kempe, Kitaev,Regev]
• 2-Dim 2-State Hamiltonian is QMAcomplete [Oliveira, Terhal]
• 1-Dim 12-state Hamiltonian is QMAcomplete.[Aharonov, Gottesman, Irani,Kempe]
The Classical Analog
• 1D MAX-2-SAT with d-state variables is in P:
- Divide line in half.
- For each d2 possible values for variables at boundary,
recursively solve n/2 variable sub-problem on each half.
- Select solution that satisfies most constraints.
• Must solve 2d2 sub-problems of size n/2
O(n
log(2 d 2 )
)
Why the difference?
• Ground state encodes the entire computation
of the quantum verifier.
• The ground state is a superposition of the
computation at each point in time.
• Can encode an extra dimension in the ground
state: time.
Translational Invariance
• 1D construction – sum of terms for each
neighboring pair of particles. Terms are
position-dependent.
Translational Invariance
• 1D construction – sum of terms for each
neighboring pair of particles. Terms are
position-dependent.
• Can the 1D construction be made
translationally-invariant?
• Translationally invariant modification that can
be used for 1D universal adiabatic computation.
[Nagaj-Wocjan, Janzin-Wocjan-Zhang]
» Degenerate
• 1D Local Hamiltonian is QMA-complete, even
what all two-particle terms are the same. [Kay]
» Requires position-dependent 1-particle terms.
Translation-Invariance
• Can we make the 1D construction
translationally-invariant with a Hamiltonian
which has a non-degenerate ground state?
– If the system is described by a single
Hamiltonian term applied to all pairs of particles
(with bounded precision), how do we encode a
circuit?...
– Show high entanglement in the ground state.
• Bounded entanglement accounts for the success of
some numerical methods [DMRG, MERA, PEPS…]
• Are there classes of systems which are guaranteed to
have ground states with low entanglement?
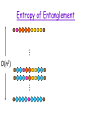
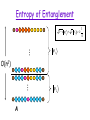
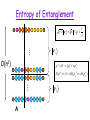
Entropy of Entanglement
• Density matrix r for the ground state of a system
of n particles.
• Let A be a contiguous subset (region) of the
particles and B its complement
rA = trB( r ).
• Entropy of entanglement for region A:
SA = S(rA) = tr(rA log rA ).
• How does entanglement entropy scale with the size
of the region or the spectral gap in the worst case?
– For 1D systems, previously known bounds, ground state
entanglment entropy scales logarithmically with the region
size.
Results
• Finite 1D chain:
– Single Hamiltonian term H that operates on two
particles of dimension 21, when applied to every
neighboring pair in a finite chain of n particles:
• Unique ground state
• Spectral gap 1/poly(n)
• The entropy of entanglement of a region of size
m on either end of the chain is W(min{m,n-m}).
[Irani, arXiv:0901.1107]
Results
• Cycles and the Infinite Chain:
– Family of translationally-invariant Hamiltonians
{Hn} for a cycle of nt 21-dimensional particles
• Spectral gap is 1/poly(n)
• For any state in the ground space of Hn, and any m, there
exist regions of size of m whose entanglement entropy is
W (min{m,n}).
– Entanglement bounds for a constant fraction of regions of
size m.
– Bounds hold in the limit as t tends towards infinity.
[Irani, arXiv:0901.1107]
1D Area Law
• Upper bound on the entanglement entropy for any
ground state of a 1D Hamiltonian H, independent of
region size but exponentially dependent on 1/D, where
D is the spectral gap of H. [Hastings 07]
• Gottesman and Hastings: is the dependence on 1/D
tight?
– Family of 1D Hamiltonians with unique ground state with
regions whose entanglement entropy is W(poly(1/D)).
– Previously, best known such lower bound was W(log(1/D))
• [Gottesman, Hatsings arXiv:0901.1108]
• Construction present here gives a similar result.
Hamiltonian Construction Basics
• Type I terms (illegal pairs)
– |ab><ab|
– Energy penalty for: ….xxxabxxxxx….
• Type II terms (transition rules)
– ½(|ab><ab| + |cd><cd| - |ab><cd| - |cd><ab|)
…xxxxabxxxx…
…xxxxcdxxxx…
Hamiltonian Construction Basics
• Type I terms (illegal pairs)
– |ab><ab|
– Energy penalty for: ….xxxabxxxxx….
• Type II terms (transition rules)
– ½(|ab><ab| + |cd><cd| - |ab><cd| - |cd><ab|)
…xxxxabxxxx…
…xxxxcdxxxx…
ab -> cd
Hamiltonian Construction Basics
1

2

3


T
Each
i
contains no
illegal pairs.
Ground State =
[Kitaev02]
1
T
T

i 1
i
Construction Overview
• Set of Transition Rules:
– Target ground state is a sequence of
states (each one transitions to the next
via a transition rule). Sequence
corresponds to a process that creates
entanglement.
• Set of Illegal Pairs:
– Ensure non-degeneracy.
• Energy penalty for any state which is not part
of the target ground state.
One Dimensional Hamiltonians
• Two types of states:
– Control states: h g f i I H
– Passive States: W w E e U u < >
• Transition rules apply to control state and a
state to the right or left.
– May move control state to the left or right.
– For example:
w f --> f W
[AGIK07]
One Dimensional Hamiltonians
• Two types of states:
– Control states: h g f i I H
– Passive States: W w E e U u < >
• Transition rules apply to control state and a
state to the right or left.
– May move control state to the left or right.
– For example:
w f --> f W
… e
e w f W E …
[AGIK07]
One Dimensional Hamiltonians
• Two types of states:
– Control states: h g f i I H
– Passive States: W w E e U u < >
• Transition rules apply to control state and a
state to the right or left.
– May move control state to the left or right.
– For example:
w f --> f W
… e
e w f W E …
[AGIK07]
One Dimensional Hamiltonians
• Two types of states:
– Control states: h g f i I H
– Passive States: W w E e U u < >
• Transition rules apply to control state and a
state to the right or left.
– May move control state to the left or right.
– For example:
w f --> f W
… e
… e
e w f W E …
e f W W E
…
[AGIK07]
Construction Overview
Circles: Single states
w
W
<
J
>
f
h
Diamonds: Two-dimensional subsystems
e+
E1
U0
g
u
I
i
Control states:
J
f
h
g
I
i
Standard basis: specify state type for each site
And then 0 or 1 for each 2D subsystem
Construction Overview
< e+ e+ e+ u+ u+ u+ w g+ W W W E+ E+ >
EPR Pairs
e+
E1
U0
u
w
W
1
1
00 
11
2
2
Entangled states
Unentangled states
Waiting states
Target Ground State
< e+ h U+ U+ W W E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ g U+ W W E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ g U+ W W E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ g U+ W W E+ >
< e+ e+ u+ g W W E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ g U+ W W E+ >
< e+ e+ u+ g W W E+ >
< e+ e+ u+ w g W E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ g U+ W W E+ >
< e+ e+ u+ g W W E+ >
< e+ e+ u+ w g W E+ >
< e+ e+ u+ w
w
g E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ g U+ W W E+ >
< e+ e+ u+ g W W E+ >
< e+ e+ u+ w g W E+ >
< e+ e+ u+ w
w
g E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ g U+ W W E+ >
< e+ e+ u+ g W W E+ >
< e+ e+ u+ w g W E+ >
< e+ e+ u+ w
w
g E+ >
< e+ e+ u+ w
w
i E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ g U+ W W E+ >
< e+ e+ u+ g W W E+ >
< e+ e+ u+ w g W E+ >
< e+ e+ u+ w
w
g E+ >
< e+ e+ u+ w
w
i E+ >
< e+ e+ u+ w
f E+ E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ g U+ W W E+ >
< e+ e+ u+ g W W E+ >
< e+ e+ u+ w g W E+ >
< e+ e+ u+ w
w
g E+ >
< e+ e+ u+ w
w
i E+ >
< e+ e+ u+ w
f E+ E+ >
< e+ e+ u+ f W E+ E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ u+ f W E+ E+ >
< e+ e+ g U+ W W E+ >
< e+ e+ f U+ W E+ E+ >
< e+ e+ u+ g W W E+ >
< e+ e+ u+ w g W E+ >
< e+ e+ u+ w
w
g E+ >
< e+ e+ u+ w
w
i E+ >
< e+ e+ u+ w
f E+ E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ u+ f W E+ E+ >
< e+ e+ g U+ W W E+ >
< e+ e+ f U+ W E+ E+ >
< e+ e+ u+ g W W E+ >
< e+ e+ u+ w g W E+ >
< e+ e+ u+ w
w
g E+ >
< e+ e+ u+ w
w
i E+ >
< e+ e+ u+ w
f E+ E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ u+ f W E+ E+ >
< e+ e+ g U+ W W E+ >
< e+ e+ f U+ W E+ E+ >
< e+ e+ u+ g W W E+ >
< e+ e+ u+ w g W E+ >
< e+ e+ u+ w
w
g E+ >
< e+ e+ u+ w
w
i E+ >
< e+ e+ u+ w
f E+ E+ >
< e+ e+ h U+ W E+ E+ >
Target Ground State
< e+ h U+ U+ W W E+ >
< e+ e+ u+ f W E+ E+ >
< e+ e+ g U+ W W E+ >
< e+ e+ f U+ W E+ E+ >
< e+ e+ u+ g W W E+ >
< e+ e+ h U+ W E+ E+ >
< e+ e+ u+ w
w
g E+ >
< e+ e+ u+ w
w
i E+ >
< e+ e+ u+ w
f E+ E+ >
…
< e+ e+ u+ w g W E+ >
< e+ e+ e+ h E+ E+ E+ >
The Hamiltonian…so far
• H = Htrans + Hlegal
• Htrans = sum of terms from transition rules as
applied to all neighboring pairs of particles.
• Hlegal = sum of terms from illegal pairs
– Will need to select these terms so that any
standard basis state outside the target ground
state has an energy penalty.
Well-Formed States
• Will assume for now that the ground
state is a superposition of bracketed
standard basis states:
– the leftmost particle will be in state < and the
rightmost particle will be in state >
<
…
>
• Will late add a term to give an energy penalty
to any state that is not bracketed.
Well-Formed States
• A state in the standard basis is wellformed if it is of the form:
<
e
…
e
h
<
e
…
e
u
<
e
…
e
u
…
u
w
<
e
…
e
u
…
u n
…
U
…
u
U
W
…
E+
…
E+
>
w
…
w
i E+
…
E+
>
…
…
w n W W E+
…
E+
>
U
…
…
E+
>
U
W
W … W E+
Can be checked by local checks…i.e. illegal pairs:
u
e
w e
[anystate] <
[Uppercase][LowerCase],….
Bad States
<
e
e
<
e
u w
<
e
e
w
u w
g
E
w
g E
>
E
E
>
e
e
u
u
u
u w
< e1
e
u
u
w w w
E
g E
>
g E0 >
• Will check for these states by showing that
they evolve (via forward or backward
application of the transition rules) to illegal
states.
Properties of Well-Formed
States
• Htrans + Hlegal is closed over the subspace
spanned by well-formed states.
– (All additional terms will be diagonal in standard
basis).
• For each well-formed state, at most one
transition rule applies in the forward
direction and at most one transition rule
applies in the reverse direction.
State Graph
• Nodes – set of all state in standard basis.
• Edges - directed edge from state A to state
B if B can be obtained by applying one
transition rule to A.
– Well-formed states are disconnected
from the rest of the graph.
– State graph restricted to well-formed
states form disjoint paths.
Hamiltonians Restricted to Paths
The Hamiltonian restricted to a
single path
H legal
 x1
0



0
0
x2

0
 0
 0 
 

 xl 
 12
 1
 2
0
Htrans  



0

0
1  12 0 
 
1
 2
1  12 0   

    

0  12 1  12 0 

0  12 1  12 

0  12 12 
1
 2
0

• If Hlegal has a non-zero entry, the minimum eigenvalue
of H restricted to the subspace spanned by states in
the path is W(1/l3) which is W(1/n6). [Kitaev 02]
• If Hlegal is all zero, the state which is the uniform
superposition of states in the path has zero energy.
Bad States
<
e
e
<
e
u w
<
e
e
w
u w
g
E
w
g E
>
E
E
>
e
e
u
u
u
u w
< e1
e
u
u
w w w
E
g E
>
g E0 >
• Will check for these states by showing that
they evolve (via forward or backward
application of the transition rules) to illegal
states.
First Round
< J U+ U+ U+ W W W >
< e+ I U+ U+ W W W >
< e+ u+ I U+ W W W >
I W W
W >
u+ w
I W
W >
u+ w
w
< e+ u+
u+
< e+ u+
< e+ u+
< e+ u+
< e+ u+
u+ w
u+ w
I W >
w w
w w
I
i
>
>
Special control states for
the first round force the
left end and the right end
to agree that it is the first
round.
Will be used to check that
state is symmetric about
center.
How To Check for Bad States:
An Example
<
e
e
e
e
u w
w f
E
>
How To Check for Bad States:
An Example
<
e
e
e
u
u w
w
<
e
e
e
e
u w
w f
w
i >
E
>
How To Check for Bad States:
An Example
<
e
e
e
u
u w
w
w
I >
<
e
e
e
u
u w
w
w
i >
<
e
e
e
e
u w
w f
E
>
How To Check for Bad States:
An Example
e
e
e I
U
U W
W
W >
...
<
<
e
e
e
u
u w
w
w
I >
<
e
e
e
u
u w
w
w
i >
<
e
e
e
e
u w
w f
E
>
How To Check for Bad States:
An Example
e
e
<
e
e
J
U U
e I
U
U W
W
W >
U W
W
W >
...
<
<
e
e
e
u
u w
w
w
I >
<
e
e
e
u
u w
w
w
i >
<
e
e
e
e
u w
w f
E
>
Need to Show:
• A path in the state graph corresponding to
the target ground state is a zero energy
state for H.
• Any standard basis state that is not
contained in a path corresponding to the
target ground state either:
• Contains an illegal pair
• Evolves via forward or backwards transitions
to a state with an illegal pair.
• Is not bracketed.
Initializing Qubits
• Hinit = | U
-
>< U
-
| Penalty for state U-
• Ensures that ground state
corresponds to a path whose initial
state has qubits set to 
…W >
< J U+ … U+ W
m
m
Enforcing Bracketed States
Hbracket = I - |
<
><
<
| -|
>
><
>
|
H = 3( Htrans + Hlegal ) + Hinit + Hbracket
– 3( Htrans + Hlegal ) term ensures there are
no bracket terms in the middle.
– Hbracket term gives an energy benefit for
having brackets at the end
…
Entropy of Entanglement
O(n2)
…
Entropy of Entanglement
…
1 c 1  c 1 , c 
1
…
2
O(n2)
A
1
4
Entropy of Entanglement
…
1 c 1  c  2 , c 
O(n2)
1
4
1
r A  (1  c) r1A  cr 2A
S ( r A )  (1  c) S ( r1A )  cS ( r 2A )
…
A
2
Finite Cycle of size tn
• Change Hlegal so that the pair
allowed.
• Well-formed states look like:
<
e
e
u g W W
E
> <
e
> <
u g W W >
is
< J U W >
• A sequence from a < to a > is a
segment.
• H is closed on the set of well-formed states
for a fixed set of segments.
Finite Cycle Cont.
• H = p(n)(Hlegal + Htrans +Hinit) + Hsize
• For p(n) large enough, using the Projection
Lemma of Kempe-Kitaev-Regev, we can
assume that the ground state of H is
composed of tensor projects of ground
states for finite chains.
• Ground state for finite chain of length l is
• Ground state for H will have form:
 l  r  s 
l
Hsize
• Hsize= (1/n)I
-| >
><
> |
+ (n-1)/Tn[| J >< J | + | i >< i | + | h >< h | ]
• Tl is the number of standard basis states in the
support of the ground state for a segment of length
l.
• l H size l  0 if and only if l=n
• Otherwise
l H size l 
1
n2
Ground States for the Finite
Cycle
<
…
n
> <
…
> <
…
> <
…
> <
…
>
n
n
n
n
• n orthogonal ground states, each a translation one
site over.
• For any region size a constant fraction of the regions
of that size have high entanglement.
• Superposition of all n states is translationally
invariant and for every region size, all regions of that
size have high entanglement.
Open Problems
• Improve gap – lower bound on entropy as
a function of 1/D.
• Area law for 2D?
• Better characterization of the
complexity of translationally invariant
systems?
• Interesting classes of Hamiltonians for
which finding ground energy is in BQP?
First Round
< J U+ U+ U+ W W W >
< e+ I U+ U+ W W W >
< e+ u+ I U+ W W W >
I W W
W >
u+ w
I W
W >
u+ w
w
< e+ u+
u+
< e+ u+
< e+ u+
< e+ u+
< e+ u+
u+ w
u+ w
I W >
w w
w w
I
i
>
>
Special control states for
the first round force the
left end and the right end
to agree that it is the first
round.
Will be used to check that
state is symmetric about
center.
How To Check for Bad States:
An Example
<
e
e
e
e
u w
w f
E
>
How To Check for Bad States:
An Example
<
e
e
e
u
u w
w
<
e
e
e
e
u w
w f
w
i >
E
>
How To Check for Bad States:
An Example
<
e
e
e
u
u w
w
w
I >
<
e
e
e
u
u w
w
w
i >
<
e
e
e
e
u w
w f
E
>
How To Check for Bad States:
An Example
e
e
e I
U
U W
W
W >
...
<
<
e
e
e
u
u w
w
w
I >
<
e
e
e
u
u w
w
w
i >
<
e
e
e
e
u w
w f
E
>
How To Check for Bad States:
An Example
e
e
<
e
e
J
U U
e I
U
U W
W
W >
U W
W
W >
...
<
<
e
e
e
u
u w
w
w
I >
<
e
e
e
u
u w
w
w
i >
<
e
e
e
e
u w
w f
E
>