* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Marvin_Weinstein
Matter wave wikipedia , lookup
Hydrogen atom wikipedia , lookup
Particle in a box wikipedia , lookup
Zero-point energy wikipedia , lookup
Dirac bracket wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
Dirac equation wikipedia , lookup
Hidden variable theory wikipedia , lookup
Quantum field theory wikipedia , lookup
Path integral formulation wikipedia , lookup
Ising model wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Wave–particle duality wikipedia , lookup
Casimir effect wikipedia , lookup
Scale invariance wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
History of quantum field theory wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Perturbation theory wikipedia , lookup
Canonical quantization wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Yang–Mills theory wikipedia , lookup
Renormalization group wikipedia , lookup
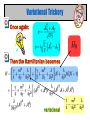
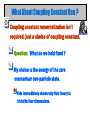
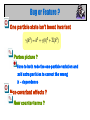
Adaptive Perturbation Theory: QM and Field Theory Marvin Weinstein Two Topics Quantum mechanics What your grandmother never told you about perturbation theory. But should have ! Field Theory Apply the QM tricks to the case of scalar field theory The Simple Harmonic Oscillator Consider usual harmonic oscillator Usual results variational The Anharmonic Oscillator The Hamiltonian is The usual problems Perturbation expansion diverges due to N! growth of the terms New result: Adaptive perturbation theory converges for all couplings and N. Variational Trickery Once again: Then the Hamiltonian becomes variational Numerical Results Trial States N=0 : N > 0: Double Well Now consider Simple variational fnctn won’t work well. But can try a shifted Gaussian Shifted Formulas The shift amounts to rewriting The Hamiltonian becomes Now vary wrt g and c Generic Behavior Tricritical behavior; i.e., 3 minima for large mass this means 1st order phase transition The Full Energy Surface Doing Better Exploit the linear term in creation and annihilation operators. In other words use a trial state of the form Varying is the same as diagonalizing the 2x2-matrix obtained by restricting the Hamiltonian to the N=0 and N=1 states. l = 1 f = 2.24… Now we have two well separated minima and no minimum at the origin l = 1 f = 2.24.. Inspect the Saddle A close inspection for this case shows that now c=0 is a local maximum. l = 1 f = 1.73.. Another View For smaller f the same is true Two separated minima, no minimum at 0. l = 1 f = 0 Still Two Minima ? 2 At first this seems surprising, but on reflection it is correct. . Tunneling Computation (even) Trial state is now The change in sign is because c -> - c Tunneling Computation (odd) Now the trial state is Re-minimize and once again we are good for ground-state and first excited state to 0.009 % Large N Still two minima, but the distance to the minimum stops growing. However the width of the wave-function keeps growing. More importantly these expection value of the x4 term keeps growing, which implies the tunneling effect increases. Sphaleron is approximately when the splitting is no longer exponentially suppressed On To Field Theory Hamiltonian in momentum space is Introduce variational parameters Expectation Value of Hamiltonian Taking the expectation value of H in the vacuum state: Differentiating wrt So Solving This clearly has a solution Actually this is an equation for m Capturing Wave-Function Renormalization Choose as the variational state We need to get the change in the vacuum energy due to this piece of Hamiltonian: What Is The Change In Energy ? To get a formula for what this does consider This is solved by iteration Taking Expectation Value Lowest energy is pole in z so So we look for a zero of the denominator Solving for z Once again we need to solve Lets redefine z So the equation becomes in the limit This Equation Can Be Solved Iteratively Define a sequence How Well Does This Work ? For a 2x2 Matrix Let and let and vary 1 Iteration More Iterations Three Iterations % Error Twelve Iterations The same is true for momentum integrals with about the same rate of convergence. Thus, the answer can always be expressed as a continued fraction. Back To Field Theory With these observations with the 4-particle contribution the vacuum energy is of the form: Diverges like L4 Minimizing Differentiating wrt yields eqn of form or Diverges like L2 Wave Function Renormalization Usual prescription We can by convention put this in a form by rescaling What About Coupling Constant Ren ? Coupling constant renormalization isn’t required, just a choice of coupling constant. Question: What do we hold fixed ? My choice is the energy of the zero momentum two-particle state. This immediately shows why this theory is trivial in four dimensions. As Before Use Resolvent Operator The k=0 two particle energy Bug or Feature ? One particle state isn’t boost invariant Parton picture ? Have to both redo the one-particle variation and add extra particles to correct the wrong k – dependence Non-covariant effects ? New counter-terms ? New Lattice Approximation ? IDEA: Now that the parameters are determined we can, in the presence of a cut-off inverse Fourier transform back to a lattice theory with coefficients which depend on the parameters. THEN DO CORE