Download Effects of Decoherence in Quantum Control and Computing

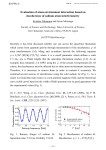
Effects of Decoherence in
Quantum Control and
Computing
Leonid Fedichkin
in collaboration with
Arkady Fedorov, Dmitry Solenov, Christino Tamon and
Vladimir Privman
Center for Quantum Device Technology,
Clarkson University, Potsdam, NY
1
Center for Quantum Device Technology
Clarkson University, www.clarkson.edu/CQDT
The main objective of our program has been
the exploration of coherent quantum
mechanical processes in novel solid-state
semiconductor information processing devices,
with components of atomic dimensions:
quantum computers, spintronic devices, and
nanometer-scale computer logic gates.
The achievements to date include new
modeling tools for evaluating initial
decoherence and transport associated with
quantum measurement, spin polarization
control, and quantum computer design, in
semiconductor device structures.
Our program has involved an interdisciplinary
team, from Physics and Electrical Engineering
to Computer Science and Mathematics, with
extensive collaborations with leading
experimental groups and with Los Alamos
National Laboratory.
Design and calculation of the reliability of
nanometer-size computer components
utilizing technology based on transport
through quantum dots.
2
Definition of Decoherence
Decoherence is any deviation of the coherent quantum system
dynamics due to environmental interactions.
Decoherence can be also understood as an error (or a probability
of error) of a QC due to environmental interaction (noise).
Application of the error-correction codes makes stable QC be
possible provided the decoherence rate is below some threshold.
Decoherence rate (the error per elementary QC cycle) must be
below
~10-6 -10-4
Proposing any QC design one must show that the decoherence
rate is below this threshold
3
Theoretical Approach of Quantifying
Decoherence




Theoretical study of decoherence usually involves an
open quantum system approach:
H= HS + HB + HI
All information of the system S including
decoherence contains in the reduced density
matrix of the reduced density matrix:
Quantum
System S
(t)=TrBR(t)
HS
To obtain (t) we need adopt some appropriate
approximation schemes.
HI
BATH
HB
However, the effect of environment onto the system cannot be
described by (t) itself. Need some numerical measure to
quantify the environmental impact to the dynamics of the
quantum system.
4
Behavior of the Density Matrix
Elements on Different Time Scales
nn (t)
T1
nm (t )
QC gate
functions
1/ C
T2
1/ 
nn ()  eEn / kT
nm()  0
/ kT
Quantum dynamics for short time
steps, followed by Markovian
2
approximation, etc.:
1  1  pure decoherence
T2 2T1
System
t
ћωD →
Rest of the
World,
Bath-mode
Bath
Interactions,
Interactions with
Impurities, Etc.
1
5
I
I
Short-time Approximation
In the short-time approximation V. Privman, J. Stat. Phys. 110, 957 (2003)
the time dependence of the overall density matrix R (t ) of the system and
bath, is given by
R(t )  ei ( HS  HB  HI )t R(0) ei ( HS  HB  HI )t .
As our short-time approximation, we utilize the following approximate
relation, expressing the exponent in the previous equation as products of
unitary operators,
e
i ( H S  H B  H I ) t O ( t 3 )
 eiH S t  2 ei ( H B  H I )t eiH S t  2 .
We now consider the approximation to the matrix element,
 mn (t )  Tr B  m  e iH S t  2 e i ( H B  H I )t e iH S t  2 R(0) eiH S t  2 ei ( H B  H I )t eiH S t  2  n  .
6
Spin-boson Model in Short-time
Approximation
•As an instructive example, we consider a general model of the twolevel system interacting with boson-modes. The Hamiltonian of the
system has the form,

H  H S  H B  H I    z   k ak†ak   x  ( g k ak†  g kak )
2
k
k
•We obtain the following expression for the density matrix of the spin
where B(t) is a spectral function defined below, L. Fedichkin, A.
Fedorov and V. Privman, Proc. SPIE 5105, 243 (2003).
1
1
 B2 (t ) 
 B2 (t ) 
  (0) 
1  e
  (0)
11 (t )  1  e
 11

 00

2
2
2
2
1
1



10 (t )  e it 1  e  B (t )  10 (0)  1  e  B (t )  01 (0).



2
2
7
Entropy and Fidelity
•The measure based on entropy and idempotency defect, also called the
first order entropy, can be defined:
S (t )    ln  , s(t )  1  Tr 2
•Both expressions are basis independent, have a minimum, 0, at pure
states and measure the degree of the state’s “purity.”
S (t )  s(t )  0   (t )   (t )  (t )
•The fidelity can be defined as:
F (t )  Tr   (i ) (t )  (t )    (i ) (t )  e iH S t  (0) eiH S t 
•The fidelity attains its maximal value, 1, provided
F (t )  1   (t )   (i ) (t )   (t )  (t )
8
Deviation Norm
We define a deviation from the ideal (without environment)
density operator according to
 (t )   (t )  ideal (t );
 ideal (t )  e iH t  (0) eiH t 
S
S
As a numerical measure we use an operator norm
   max i 
i
In case of two-level system it is
Properties:
    00   01 .
2
2
   0   (t )   (i ) (t )
and symmetric in (t) and (i)(t).
9
Measures of Decoherence at
Short Times
All measures depend not only on time but also on the initial
density matrix (0). For spin-boson model they are,
L.Fedichkin, A. Fedorov and V. Privman, Proc. SPIE 5105, 243 (2003). :


1
2
2
2 B 2 ( t ) 
2
1  e
   (0)   (0)   4  (0) sin [( 2)t   ] 
01
0
11
00

2 
2
1
2
2

1  F (t )  1  e  B (t )   11 (0)  00 (0)   4 01 (0) sin 2 [( 2)t   0 ] ,

2
1 2
1
2
2
 B2 (t ) 
2
   (0)   (0)   4  (0) sin [( 2)t   ]
 (t )   1  e
.
01
0
11
00


2
s(t ) 




At t=0, the value of the norm is equal to 0, and then it
increases to positive values, with superimposed modulation
at the system’s energy-gap frequency.
10
Maximal Deviation Norm D(t)
The effect of the bath can be better quantified by D(t)
D(t )  sup(  (t  (0))  )
 (0)
Provides the upper bound for decoherence which does not
depend on initial conditions.
This measure is typically increase monotonically from 0,
saturating at large times at a value D()  1. For spin-boson
model it is, L. Fedichkin, A. Fedorov and V. Privman, Proc. SPIE
5105, 243 (2003).
1
 B2 ( t ) 
 , for short times
D(t )  1  e


2
D(t )  1  et / T1 , for large times assuming T1 =T2 /2
11
The Maximal Norm and Its
Properties
0.5
Averaging over the initial
density matrices removes
time-dependence at the
frequencies of the system,
leaving only the relaxation
temporal dynamics
0.4
D(t)
0.3

0.2
0.1
0.0
t
The evaluation of system dynamics is complicated for multi-qubit
systems. However, we established approximate additivity that
allow us to estimate D(t) for several-qubit systems as well.
12
Additivity for Multiqubit
System
Entanglement is crucial for quantum computer:
 (0)  1 (0)  2 (0)  ...   N (0)!
D is asymptotically additive for weakly interacting even initially
entangled qubits, as long as it is small (close to 0) for each, namely for
short times. This is similar to the approximate additivity of relaxation
rates for weakly interacting qubits at large times, L. Fedichkin, A.
Fedorov and V. Privman, cond-mat/0309685 (2003).


 N

1
 Bq2 ( t )
DS (t )   Dq (t )  o   Dq (t )  , Dq (t )  1  e
.
2
q
 q

N
This property was established for spin-boson model with two types
of interaction. The sum of the individual qubit error measures
provides a good estimate of the error for several-qubit system.
13
Alternative Approach to Quantum
Information Processing: Quantum
Walks
The Influence of Decoherence on
Mixing Time in Quantum Walks
on Cycle Graphs
14
Motivation



New family of quantum computer algorithm:
quantum walks based algorithms (3rd after
quantum Fourier transform and Grover’s
iterations)
Quantum walks may be easier to realize in
experiment
What effect does decoherence produce on
algorithm?
15
Hitting times
How long does it take for the walk to reach a
particular vertex?
More precisely, we say the hitting time of the
walk from a to b is polynomial in n if for some
t=poly(n) there is a probability 1/poly(n) of
being at b, starting from a.
16
Hitting times: quantum vs. classical
Theorem: Let Gn be a family of graphs with
designated ENTRANCE and EXIT vertices.
Suppose the hitting time of the classical random
walk from ENTRANCE to EXIT is polynomial in n.
Then the hitting time of the quantum walk from
ENTRANCE to EXIT is also polynomial in n (for a
closely related graph).
Farhi, Gutmann 97
17
Experimental Realizations
Electron Coupled Double-Phosphorus Impurity in Si
L.C.L. Hollenberg, A.S. Dzurak,
C. Wellard, A.R. Hamilton, D.J.
Reilly, G.J. Milburn, and R.G.
Clark, Phys. Rev. B 69, 113301
(2004)
18
Experimental Realizations
Gate-engineered Quantum Double-Dot in GaAs
T. Hayashi, T. Fujisawa, H.-D.
Cheong, Y.-H. Jeong, Y. Hirayama,
Phys. Rev. Lett. 91, 226804 (2003)
19
Experimental Realizations
Gate-engineered Quantum Double-Dot in GaAs with QPC
M. Pioro-Ladriere, R. Abolfath, P. Zawadzki, J. Lapointe, S.A. Studenikin,
A.S. Sachrajda, P. Hawrylak, cond-mat/0504009
20
Sketch of possible realization of system
considered
21
Structure of each vertex
22
System description
N 1
N 1
j 0
j 0
H  H Graph   H Det , j   H Int , j
H Graph
1 N 1 

  c j 1c j  c j c j 1 ;
4 j 0


cN  c0

H Det , j   El , j al, j al , j   Er , j ar, j ar , j   lr , j al, j ar , j  ar, j al , j
l
r
lr

H Int , j    c c a a  a a

lr , j j j

l, j r, j

r, j l, j

lr
23

Sketch of the graph and its density matrix
evolution
0
1
N-1
2
N-2
...
...
N/2
d
i
 ,    , 1   1,   1,   , 1    1   ,   ,
dt
4
24
Mapping of quantum walk on cycle on
classical dynamics of real variable Sαβ on torus
0
1
N-1
2
 1  N  0
 1  N  0
  1  1  N  1
  1  1  N  1
N-2
..
.
..
.
N/2
β
S ,   , i  a
Sα,β+1
Sα-1,β
Sα+1,β
Sα,β-1
α
d
1
S ,   S , 1  S 1,  S 1,  S , 1    1   ,  S ,
dt
4
25
The expression for Sαβ at small decoherence
rates
 N 1

exp  
t 1  O     

N


S ,  (t )   ,  
N
N2
N 1

2 k 2 ik     
2
1




exp
it
sin

 k ,0 2k , N  
 1 O  

N
N
k 0







 N 2

exp  
t 1  O      N 1 N 1
N



1   k ,m 1   k  m , N  


2
N
k 0 m 0

  k  m    k  m  2 i  k  m  
2
 exp  it cos
sin

 1 O  
N
N
N







26
The probability to find particle at vertex N/2
0.1
SN/2,N/2
0.08
N=10
=0.01
0.06
0.04
0.02
t
50
100
150
200
250
300
Green and blue curves are exponents with the rates
(N-1)/N and (N-2)/N correspondingly.
27
The probability to find particle at vertex N/2
0.06
0.05
SN/2,N/2
0.04
N=100
=0.01
0.03
0.02
0.01
t
50
100
150
200
250
300
Blue curve corresponds to the exponent with the rate (N-2)/N
28
Probability distribution along the cycle as
function of time with (B) and without
decoherence (A)
29
Classical dynamics (high decoherence rate)
t0
500
4
8
12
250
16 19
500
250
0
0
4
8
12
0#
16 19
30
Quantum dynamics (low decoherence rate)
t0
50
4
8
12
16 19
50
25
25
0
0#
16 19
0
4
8
12
31
Norm of Deviation from Mixed
Distribution and its the upper bound
32
Mixing time vs. decoherence rate
33
Mixing time vs. decoherence rate
(loglog-scale)
Upper and lower bounds for N=35 are shown
34
Probability distribution along the hypercycle as function
of time with large (B) and small decoherence (A)
N=3, n=3
35
References







D. A. Meyer, On the absence of homogeneous scalar unitary cellular
automata, quant-ph/9604011
D. Aharonov, A. Ambainis, J. Kempe, and U. Vazirani, Quantum walks on
graphs, quant-ph/00121090
E. Farhi and S. Gutmann, Quantum computation and decision trees, quantph/9707062
A. M. Childs, E. Farhi, and S. Gutmann, An example of the difference
between quantum and classical random walks, quant-ph/0103020
C. Moore and A. Russell, Quantum walks on the hypercube, quantph/0104137
A. M. Childs, R. Cleve, E. Deotto, E. Farhi, S. Gutmann, and D. A.
Spielman, Exponential algorithmic speedup by quantum walk, quantph/0209131
H. Gerhardt and J. Watrous, Continuous-time quantum walks on the
symmetric group, quant-ph/0305182
36
References
D. Solenov and L. Fedichkin, Phys. Rev. A, in press; quantph/0506096; quant-ph/0509078.
 A. Ambainis, Quantum walks and their algorithmic
applications, quant-ph/0403120.
 S. A. Gurvitz, L. Fedichkin, D. Mozyrsky, G. P. Berman, Phys.
Rev. Lett. 91, 066801 (2003).
 L. Fedichkin and A. Fedorov, Phys. Rev. A 69, 032311 (2004).
 A. Fedorov, L. Fedichkin, and V. Privman, cond-mat/0401248,
cond-mat/0309685, cond-mat/0303158.
 L. Fedichkin, D. Solenov, and C. Tamon, Quantum Inf. Comp.,
in press; quant-ph/0509163.

37
Summary I

We consider one possible approach to quantify decoherence by
maximal deviation norm. The useful properties such as
monotonic behavior were demonstrated explicitly on the
example of two-level system.

We established additivity property of this measure of
decoherence for multiqubit system at short times. It allows
estimation of decoherence for complex systems in the regime of
interest for quantum computing applications.
38
Summary II






The concept of quantum walks can be used to build new
family of efficient quantum algorithms
Devices with quantum walks behavior can be created by
using nowadays technology
The architecture of quantum walks quantum computer
could be simpler than that of standard quantum computer
We have developed and applied a new approach to
evaluation of the effect of decoherence on quantum walks.
The density matrix is approximated by explicit formula
asymptotically exact for small decoherence rates
The dependence of mixing time vs decoherence rate is
nontrivial: small decoherence can help!
39