* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Statistical Mechanics
ALICE experiment wikipedia , lookup
Quantum logic wikipedia , lookup
An Exceptionally Simple Theory of Everything wikipedia , lookup
Quantum potential wikipedia , lookup
Uncertainty principle wikipedia , lookup
Photoelectric effect wikipedia , lookup
Relational approach to quantum physics wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Nuclear structure wikipedia , lookup
Spectral density wikipedia , lookup
Bremsstrahlung wikipedia , lookup
Renormalization wikipedia , lookup
Renormalization group wikipedia , lookup
Dirac equation wikipedia , lookup
Quantum tunnelling wikipedia , lookup
Density matrix wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Quantum chaos wikipedia , lookup
Probability amplitude wikipedia , lookup
Quantum state wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
Wave function wikipedia , lookup
Wave packet wikipedia , lookup
Bose–Einstein statistics wikipedia , lookup
ATLAS experiment wikipedia , lookup
Electron scattering wikipedia , lookup
Photon polarization wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Double-slit experiment wikipedia , lookup
Old quantum theory wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Canonical quantization wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Standard Model wikipedia , lookup
Grand Unified Theory wikipedia , lookup
Elementary particle wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Statistical Mechanics
quantum statistics
Rayleigh-Jeans formula
Planck radiation law
“Very strange people, physicists - in my experience the ones who aren't
dead are in some way very ill.”—Douglas Adams
Error in syllabus:
skip section 8 (in addition to sections 7 and 11)
“Testable” sections from chapter 9: 1 through 6, 9, 10.
9.4 Quantum Statistics
Here we deal with ideal particles whose wave functions overlap.
We introduce quantum physics because of this overlap.
Remember:
n ε = gε f ε
The function f(ε) for quantum statistics depends on whether or
not the particles obey the Pauli exclusion principle.
“The wierd thing about the half-integral spin particles (also known as
fermions) is that when you rotate one of them by 360 degrees, it's
wavefunction changes sign. For integral spin particles (also known as
bosons), the wavefunction is unchanged.” –Phil Fraundorf of UMSL,
discussing why Balinese candle dancers have understood quantum
mechanics for centuries.
Recall that electrons and other particles with half-integral spin
(1/2, 3/2, 5/2, etc.) are fermions and obey the Pauli exclusion
principle.
The wave function of a system of fermions is antisymmetric
because it changes sign upon the exchange of any pair of
fermions. We will find that fermions follow Fermi-Dirac
statistics.
Recall also that photons and other particles with integral spin
(0, 1, 2, etc.) are bosons and are not subject to the Pauli
exclusion principle.
The wave function of a system of bosons is symmetric because
it sign remains unchanged upon the exchange of any pair of
bosons. We will find that bosons follow Bose-Einstein statistics
Let’s refresh our memory on symmetric and antisymmetric wave
functions. Much of this discussion (everything inside the yellow
boxes) is a repeat of lecture 24.
Consider two identical particles (1 and 2) which may exist in
two different states (a and b).
I = a (1) b (2)
II = a (2) b (1)
If the particles are indistinguishable, then we cannot tell
whether the system is in state I or II, and, because both
states are equally likely, we write the system wave function as
a linear combination of I and II.
If the particles are bosons, the system wave function is
symmetric:
1
B =
a (1) b (2) + a (2) b (1) = S
2
If the particles are fermions, the wave function is
antisymmetric:
1
F =
a (1) b (2) - a (2) b (1) = A
2
What happens if we try to put both particles 1 and 2 in the
same state?
If the particles are distinguishable, we can simply write
M = a (1) a (2) .
The subscript M indicates Maxwell-Boltzmann statistics,*
because the particles are distinguishable.
The probability density for distinguishable particles is
M*M = a (1)* a (2)* a (1) a (2) .
*“Huh? I thought you said Maxwell-Boltzmann statistics is for
classical (not quantum) particles. How come the wave
functions?”
Be quiet! Actually, recall that you can always use QM. You
usually don’t use QM unless you have to. In this case, it is
useful for comparing MB results with quantum statistics.
For bosons
B =
2 a (1) a (2) .
with a probability density
B *B = 2 a (1)* a (2)* a (1) a (2)
B *B = 2 M*M .
In other words, if the particles are bosons, they are twice as
likely to be in the same state as distinguishable particles!
On the other hand, if the particles are fermions,
1
F =
a (1) a (2) - a (2) a (1) ,
2
with a probability density
F * F = 0 .
If the particles are fermions, it is impossible for both particles to
be found in the same state.
In general, the presence of a boson in a particular quantum
state increases the probability that other bosons will be found in
the same state…
…but the presence of a fermion in a particular quantum state
prevents other fermions from being in that state.
We are now (almost) ready to write down the distribution
functions for bosons and fermions.
Remember, the distribution function gives the probability that a
state of energy is occupied by a particle.
For bosons, we use a function called the Bose-Einstein (BE)
distribution function.
In 1924, Indian physicist S. N. Bose submitted a
paper using statistical mechanics and the idea of
light quanta to explain Planck’s radiation law. The
paper was rejected. Einstein translated the paper,
got it accepted, and extended Bose’s ideas from
photons to other particles. Bose’s paper removed
any final objections to the photon theory of light.
Bose
For fermions, we use a function called the Fermi-Dirac (FD)
distribution function.
In 1926, Enrico Fermi and Paul Dirac independently
realized that the Pauli exclusion principle leads to a
different kind of statistics for fermions (including
electrons). Dirac shared the 1933 Nobel prize with
Schrödinger.
Dirac was a brilliant mathematician. Sometimes it
seems like all the great mathematicians of the 1930’s
worked on problems involving quantum mechanics.
Dirac
Dirac was famous for saying exactly what he meant, and no more (typical
mathematician?). Once when someone, making polite conversation at
dinner, commented that it was windy, Dirac excused himself, left the table
and went to the door, looked out, returned to the table and replied that
indeed it was windy.*
When Dirac won the 1933 Nobel prize, he decided to turn it down because
he hated publicity. When it was pointed out he would receive far more
publicity by turning it down, he changed his mind.
*http://www-groups.dcs.st-and.ac.uk/history/Mathematicians/Dirac.html
For bosons, the distribution function is
fBE (ε) =
the difference
1
e e
ε / kT
-1
.
For fermions, the distribution function is
fFD (ε) =
1
e e
ε / kT
+1
.
These were derived in an appendix in the previous edition of
Beiser, but are just given as truth here.
Remember, bosons are particles with integral spins. There is no limit on the number of bosons
which may occupy any particular state (typically the ground state). Examples are photons in a
cavity, phonons, and liquid 4He.
Also remember, fermions are particles with half integral spin, with only one particle per state n,
ℓ, mℓ, ms. The +1 in the denominator of f(ε) means that the f(ε) is never greater than 1.
Examples are free electrons in metals and nuclei in collapsed stars.
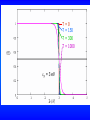
The Fermi-Dirac Distribution Function
fFD (ε) =
1
e eε / kT +1
The Fermi energy εF is the energy at which fFD = 1/2. From the
above equation we see that εF = -kT, and we can write fFD as
fFD (ε) =
1
e
ε - ε F / kT
+1
blowing up the size a bit
so you can see better
On the next slide is a plot of the Fermi-Dirac distribution
function at T=0, 150, 300, and 1000K.
T=0
T = 150
T = 300
T = 1000
F = 3 eV
Here’s a comparison of our three distribution functions.
Bosons “like” to
be in the same
energy state, so
you can cram
many of them in
together.
Fermions don’t
“like” to be in the
same energy
state, so the
probatility is the
least.
When bosons get very cold, they all fall into the same (lowest)
energy state. Their wave packets merge and form a single
wave packet. If the bosons are atoms, the individual atoms
lose their identity and form a “super atom.”
Cornell and Wieman of U. Colorado and Ketterle won the 2001
Nobel prize for making a Bose-Einstein condensate out of 2000
rubidium atoms.
They had to cool the atoms to 0.000001 K to do this.
Formation of the BEC…
The BEC is a new state of matter.
BEC : ordinary matter :: laser : light bulb light.
Practical applications of BEC: none yet. (Who knows…)
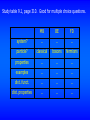
Study table 9.1, page 310. Good for multiple choice questions.
MB
BE
FD
system?
…
…
…
particle?
classical
bosons
fermions
properties
…
…
…
examples
…
…
…
dist. funct.
…
…
…
dist. properties
…
…
…
9.5 Rayleigh-Jeans Formula
“OK, this quantum statistics stuff has some pretty math in it,
but what good is it?”
We’ll find we need to use Fermi-Dirac statistics to “explain”
properties of metals and semiconductors.
Bose-Einstein statistics “explains” blackbody radiation.
We talked about blackbody radiation in chapter 2 (lecture 5).
You should review those notes.
A blackbody is the best possible absorber / emitter of radiation.
The spectrum of blackbody radiation depends only on the
temperature of the blackbody.
This is nice because you don't need to worry about the details
of the composition of the blackbody.
A box with a hole in it
makes a good
laboratory approximation to a blackbody
emitter.
Plotted to the right are
a couple of spectra for
blackbodies at different
temperatures.
John William Strutt (Lord Rayleigh)
tried to calculate this classically.
To calculate the spectrum of radiation
from a blackbody, consider a box with a
hole in it.
Radiation can get in the hole. It then reflects back and forth
inside the cavity.
a spherical cavity turns out to
be the best device for
experimentally realizing
blackbody radiation
We've discussed this problem before in several different
contexts. If the radiation interferes destructively, it will never
get out. We only see radiation (waves) getting out that were
able to set up standing waves inside the cavity.
Our job is thus to determine what kinds of standing waves can
exist in the cavity, and what their energies are.
It is not difficult, but it is somewhat tedious, to calculate the
number of standing waves allowed for any particular frequency
interval. This is the result:
g f df =
8L3
c3
f 2 df ,
where g(f)df is the number of standing waves ("modes")
between f and f+df, and L3 is the cavity volume. Note that the
number of modes is proportional to f2.
The details of this derivation are worthwhile if you are going to
study solid state physics at a more advanced level. I won't test
you on the derivation in this class.
You can calculate the density of standing waves by dividing the
above result by the volume, L3.
To get the energy density (energy per unit volume), simply
multiply g(f) by the energy of an oscillator of frequency f (we
assume the waves originate in oscillators in the cavity walls).
Remember, kT/2 goes with each degree of freedom, and an
oscillator has two degrees of freedom, so multiply by kT.
The spectral energy density is thus
u f df =
8 f 2 kT
c
3
df .
This is called the Rayleigh-Jeans formula
because British mathematician and
astronomer James Jeans corrected a small
mathematical error in Rayleigh’s work.
That’s 1
point off
for a math
error.
We’ve already seen (chapter 2) how well this works.
The formula leads to the
"ultraviolet catastrophe." It
predicts increasing energy
density with increasing f. It
doesn't match experiment at
all. It doesn't even come
close. Something is seriously
wrong.
theory
experiment
Rayleigh produced a lifetime of brilliant work. He won the Nobel prize in
1904 for discovering the inert gas argon. However, as Beiser points out,
Rayleigh’s most important contribution to physics may have been this
disastrous theory of blackbody radiation. Rayleigh died never really
accepting the quantum theory of light.
“An important scientific innovation rarely makes its way by gradually winning over
and converting its opponents…What does happen is that its opponents gradually die
out”—Max Planck.
9.6 Planck Radiation Law
In the last section we derived the Rayleigh-Jeans formula for
the spectral energy density for blackbody radiation. We found
that it failed miserably.
What's wrong with the Rayleigh-Jeans formula?
Rayleigh divided up the energy into kT/2 for each degree of
freedom. This is fine for a continuous energy distribution.
We now know that it doesn't work for harmonic oscillators,
where energy is quantized in units of hf. Therefore, our energy
density was wrong.
Our density of standing wave modes,
g f df =
8L3
c3
f 2 df ,
as calculated above is OK.
To get the correct energy density of photons in the cavity, we
multiply our density of modes by the energy of each mode and
the probability as a function of T that a mode is occupied.
u f df = energy of mode × density of modes
× probability that mode is "occupied"
u f df = hf G f fBE f df
u f df =
8h
c
3
f3
e
hf / kT
-1
df
Warning—two different f ’s;
might be better to use for
frequency here.
The last equation on the previous slide is called the Planck
radiation formula, and it works very well. Plug it into Mathcad
and try it some time.
Note that was set equal to 0 in Bose-Einstein distribution
function, which was used in the equation above.
is a constant which, mathematically, “says” that the number
of particles is conserved. If we don't require conservation of
particles, we set =0.
Wien's displacement law
You can calculate the wavelength at the peak of the energy
density by expressing u as a function of wavelength and taking
the derivative.
u f df =
8h
c
3
f3
e
hf / kT
-1
df
Use c = f to write u = u() and set 0 = du /d to find for
maximum. The result is Wien's displacement law:
λ max T = 2.898×10-3 m K .
at which u is maximum!
not maximum in spectrum!
Wien's displacement law tells which
way the peak in the blackbody
spectrum shifts as the temperature
changes.
You can write a formula for u(f) as we did, or for u(). The
plots look similar:
But the Rayleigh-Jeans formula blows up as f and as
0 (can be visually confusing!).
Also, the peak in the spectrum shifts towards higher f as T
increases, but to lower .
In these plots, B corresponds to our u and corresponds to our f.
Homework problem 9.31 The brightest part of the spectrum
of the star Sirius is located at a wavelength of 290 nm. What is
the surface temperature of Sirius?
λ max T = 2.898×10-3 m K
2.898×10-3 m K
T=
λ max
2.898×10-3 m K
T=
290×10-9 m
T = 9990 K
Aren’t stars hotter than this? Yes—interior temperatures, and temperatures
a short distance above the surface, reach millions of degrees.
Applications:
Portable, variable temperature blackbody
radiation source for precision calibration of
radiation thermometers.
Portable thermal imager.
Anybody here have children?
Whey you do, they come with a sickness guarantee.
They are guaranteed to get sick. Then
you have to take their temperature.
Sure. Ever tried to get a screaming 2year old to hold a thermometer in his
(her) mouth? Taking a sick toddler’s
temperature is a 2-parent job. Enough
said.
Or you can get one of these. Worth every
penny of the $35-40 it costs.
No, I am not affiliated with any
thermometer company!
The Stefan-Boltzmann Law
The total energy density inside the cavity is found by integrating
the energy density over all frequencies.
utotal =
0
8h
f3
c3
ehf / kT -1
The result is proportional to T4.
df = a T 4 .
a constant
The Stefan-Boltzmann law says R=eσT4, where R is the radiated
energy per second per unit area, and e is the emissivity of the
radiating surface, and σ is a constant (see Beiser for the value
of σ).
Homework problem 9.26 If a certain blackbody radiates 1
kW when its temperature is 500 ºC, at what rate will it radiate
when its temperature is 750 ºC?
R = eσ T 4
at 500 o C :
some of the other
at
problems for this
material are more
complex, but are still
fair game for the exam
T
R 2 = R1
T
4
2
4
1
R1 = eσ T14
750 o C :
R 2 = eσ T24
R 2 eσ T24
=
R1 eσ T14
don’t forget!
750 +273
T2
= R1 = 1 kW
T1
500 +273
4
R 2 = 3.05 kW .
4
Global Warming?
It is a fact that human activity has put enormous amounts of
“extra” CO2 into the atmosphere since the beginning of the
industrial revolution.
It is also a fact that CO2 is a
greenhouse gas.
There exists extensive data which
suggests the earth is warming.
Much of the data is subject to
interpretation. (i.e., one might say
“yes, warming,” or one might say
“coincidence, not proof.”
My sense is that “most” scientists believe something is truly
going on. Some very emphatically. Others less so.
What will be the result of increasing earth temperature? We
don’t know. There will be change. Perhaps dramatic. Perhaps
not in the direction we might predict. How do you feel about
change?
Global warming is intimately connected to blackbody radiation
and the Stefan-Boltzmann law.
Opinion: those running our government need to learn more
physics.
Consider designing a cryostat or furnace. What things would
you worry about? What would you do to make the cryostat or
furnace work well?