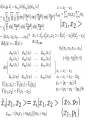Download Multiparticle Quantum: Exchange

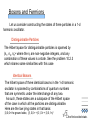
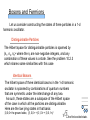
Beyond one particle in one dimension
Treating many particles
Particles moving in two, three- and more (!)
dimensions
Role of exchange in case of identical particles
Generalizing to the multiparticle case
We had for the one-particle and one-dimensional case before that
The one particle wavefunction
In co-ordinate basis, we can think of it as
But, this was without thinking about the activity of other particles, which we
presume are independent of this particle. That is fine, but clearly we are interested
in systems with many particles and especially in systems in which there is an
interaction between the particles. How do we start to talk about those cases?
If the particles really are independent and in a sense imagine them far apart
spatially, then we want to imagine simply that we can write down a single
particle wave function for each one, say
and
But this is not adequate for several reasons...we need to understand this as a
description of a single vector (a joint wave function) in a single hilbert space.
(x)
Two particles....
Imagine the case of just two particles. They could be different particles, it
doesn't matter. Let
represent the 1-particle wave function of the first particle. It is a
vector in Hilbert space
1
be a wave function associated with the other particle ...it is a
vector in a different Hilbert space, say
Together the most simple way to
2 understand a
joint Hilbert space is one in which we form 2-ples of vectors; in symbols,
.
Where the state would be
1.)
. Note two important consequences
of this choice;
=
1
2
i.e. It is important to realize that this means we are not just adding vector directions
to one of the spaces....technically this is called a tensor product and is not a
direct sum of vector spaces
2.) The operators on the separate Hilbert spaces can be thought of as acting
in that they only act on their factor, and are 1 on the other factor.
on the full
Two particles....
Stop and think: The joint Hilbert space is not the direct sum
BUT the product
Ex: Suppose both
=<x,y,z> are three
dimensional
Then the full Hilbert space is spanned by 9 elements:
|ax>, |ay> , |az>,
,|cx> , |cy>, |cz>.
|bx> ,|by>, bz>
1
=<a,b,c> and
2
SO it cannot be the direct sum, which would only have a
6-dimensional basis!
Two particles....
This is reasonable and sensible in light of the fact that as operators on the full
Then we have implemented the commutator relations called the canonical
commutation relations (CCR)
Where the 'i' and 'j' label the part of the space the operator is acting on. In what
follows we will be dropping the hats almost completely except where it might
cause confusion, mostly to simply the notation and emphasize only the index
describing which part of the full hilbert space the operator is acting on.
SPECIAL NOTE: there is no guarantee that all the operators on the big hilbert
space can be written in terms of operators on each factor as we are discussing!
But we focus on this anyways for reasons of clear exposition only...
So, for example, let |x1,x2> be a position basis of states in the full
Hilbert space the action of the x-operators are thus,
The fact that the xi all commute with each other is consistent with
our ability to write the full state this way (simultaneous diagonalization).
And the inner product in the co-ordinate basis in the full Hilbert space can
be written this way
Note, oddly, that this choice does depend on the fact that
we have chosen cartesian co-ordinates.
Special Note
In the full Hilbert space there are states that are not simple
products of states in the separate factors. For example,
|3,4> + |1,2>
Where '1,2,3,4' are separate positions, 1 and 3 of the
first particle and 2 and 4 of the second particle.
Such a state is called “Entangled”
Two particles....
Of course for the multiparticle system we still need
to solve:
Where the Hamiltonian must make sense for each particle independent
of the other. This means that essentially the most complicated Hamiltonian
we could have would be
For a two particle hilbert space (all in 1-d) we often come across two types of
problems;
1.) Separable case:
As would be the case for which
2.) Inseperable case: when the H doesn't split as above. These cases can be quite
complicated, generally intractable analytically.
Two particles....
Separable case- almost trivial one:
through
SO: solve each system '1' and '2' separately and combine the
Hilbert spaces. Done !
Separable Case – for simple interaction
if
For
center of mass & relative co-ordinates. Define;
doesn't look separable until
we go to
Two particles....
Separable Case – for simple interaction (con't)
To keep the CCR, such as
We take
Then the Hamiltonian can be written as
And, lo, it is separable! So the wave function is, in co-ordinates, |xcm, x> = A(xcm)B(x)
where in the center of mass co-ordinate the solution A(xcm) is a plane wave (like the
example of the translating gaussian minimum uncertainty packet of the last lecture.
The B(x) is a solution of the 1-d schroedequation in the potential V(x) but as a
massive particle of mass
Three particle case
For simplicity, take all the masses the same, m (but this can be
generalized to different m's
In addition to the usual center of mass and total momentum,
One simple relative
co-ordinate
We take
...causes this to be
the other one
and..
So that the CCR are still true,
etc...in
Three particle case
Note further that
So that the kinetic energy part of the Hamiltonian remains separable in these
co-ordinates. Generally that will not be true of the inter-particle potential, though
there is a special case! Once again in the (isotropic) harmonic oscillator case the
potential energy in these co-ordinates is still separable;
N-particle case
Consider the case of N particles that we assume individually interact weakly
with an external field but do interact more strongly with one another. In that
case it is useful to separate out the center of mass motion and total momemtum
from the other 'internal' degrees of freedom.
Note that from the underlying CCR on the 'fundamental' DOF xi and pj
We will have that
N-particle case
Said another way, the commutator has not scaled away! Going to a large number of
particles has not made the commutator vanish. The xcm and pcm of the
ensemble, macroscopic quantities though they may be, are constrained by the
same quantum mechanical relations and limits as the microscopic degrees of
freedom.
Simply, we cannot think of quantum as only applying to the small !
Quantum properties persist at all scales and the separation of the center of mass
motion is, for example, an example of why we can write down a quantum
mechanical description of a proton although we know that it is made up of
many particles.
Multi-dimensional case: single particle
Here, the CCR reduce to the same CCR for the multiparticle
case in 1-d, a case we already know how to handle. The upshot
here is that since x,y,z co-ordinates are assumed to commute,
the vectors in the Hilbert space for a single particle in 3-d can
be thought (loosely) as functions of three variables. Rather than
have a theoretical discussion here about this, we remind about
the development of the Hamiltonian in 3-d in the “Postulates”
lecture several weeks ago and build up intuition in this case
in the section on the Hydrogen atom that will be coming
up soon!!
What does it mean in QM for
two particles to be identical?
Return to the two particle case. If we have two identical particles,
then quantum mechanics indicates that there is no test or
measurement we can perform to distinguish them. We cannot
even distinguish them by following their trajectories.
Let the one-particle wave functions for each particle be written
|a(x1)> and |b(x2)> if they were independent, distinguishable
particles so that we could even talk about the one-particle wave
functions. In the full Hilbert space then we could write the
state |a(x1)b(x2)> were they distinguishable.
What if they are they are identical particles. Then, no matter where they are
or what they are (individually) doing, there is no way to distinguish the state
|a(x1)b(x2)> from the state |b(x1)a(x2)>.
NOTATION:
|ab> = |a(x1)b(x2)> , reading the factors in the multiparticle state from left to right in their
position dependence.
What does it mean in QM for
two particles to be identical?
Being identical particles must mean that the state |ab> and the state
|ba> are physically the same; as vectors in Hilbert space then they
must be proportional
|ab> =
|ba>
where
is a phase
Of course, interchanging two particles can be thought of actively,
as an operator on the full Hilbert space. It is a linear operator.
So, we can think of the above statement as a definition of the
exchange operator in the Hilbert space. We can thus interchange
the particles twice, finding
|ab> =
|ab>
And so
must be +1 or -1
Bosons and Fermions
=1 Bosons. So the WF can be written (|ab>+|ba>)/
= -1 Fermions. So the WF can be written (|ab> - |ba>)/
In nature each body is either a Boson or Fermion
Identical bosons can have the same wavefunction (and
thus the same quantum numbers)
Fermions never have the same (one-particle) wave function
(state is identically zero if a=b)
Bosons and Fermions
=1 Bosons. So the WF can be written (|ab>+|ba>)/
Photon, higgs, gauge bosons (W+/-, Z0), 87Rb, 85Rb, 23Na, Buckeyball,
Phonon, gluons, graviton (?), meson,
= -1 Fermions. So the WF can be written (|ab> - |ba>)/
Proton, neutron, electron, 86Rb, quark, neutrino, muon
In nature each body is either a Boson or Fermion
Identical bosons can have the same wavefunction (and
thus the same quantum numbers)
Fermions never have the same (one-particle) wave function
(state is identically zero if a=b)
Bosons and Fermions
=1 Bosons. So the WF can be written (|ab>+|ba>)/
Photon, higgs, gauge bosons (W+/-, Z0), 87Rb, 85Rb, 23Na, Buckeyball,
Phonon, gluons, graviton (?), meson,
Bose-Einstein Condensates
= -1 Fermions. So the WF can be written (|ab> - |ba>)/
Proton, neutron, electron, 86Rb, quark, neutrino, muon
Fermi Pressure
In nature each body is either a Boson or Fermion
Identical bosons can have the same wavefunction (and
thus the same quantum numbers)
Fermions never have the same (one-particle) wave function
(state is identically zero if a=b)
Bosons and Fermions
Ex 1: from Modern Class or your chemistry class:
The angular momentum possible in homonuclear molecules...Either
all even (bosons) or
All odd (fermions) multiples of
Ex 2: Note that < fermion | boson> =0 always.
Bosons and Fermions
Let us consider constructing the states of three particles in a 1-d
harmonic oscillator.
Distinguishable Particles
The Hilbert space for distinguishable particles is spanned by
|n1, n2, n3> where the ni are non-negative integers, and any
combination of these values is a state. See the problem 10.2.3
which shares some similarities with this case
Identical Bosons
The hilbert space of three identical bosons in the 1-d harmonic
oscilator is spanned by combinations of quantum numbers
that are symmetric under the interchange of any two.
As such, these states are a subspace of the Hilbert space
of the case in which all the particles are distinguishable.
Here are the low lying states in that basis:
|0,0,0> the ground state, (|1,0,0> + |0,1,0> + |0,0,1>)/
is the first excited state.
Bosons and Fermions
Let us consider constructing the states of three particles in a 1-d
harmonic oscillator.
Distinguishable Particles
The Hilbert space for distinguishable particles is spanned by
|n1, n2, n3> where the ni are non-negative integers, and any
combination of these values is a state. See the problem 10.2.3
which shares some similarities with this case
Identical Bosons
The hilbert space of three identical bosons in the 1-d harmonic
oscilator is spanned by combinations of quantum numbers
that are symmetric under the interchange of any two.
As such, these states are a subspace of the Hilbert space
of the case in which all the particles are distinguishable.
Here are the low lying states in that basis:
|0,0,0> the ground state, (|1,0,0> + |0,1,0> + |0,0,1>)/
is the first excited state.
Bosons and Fermions
Identical Bosons (con't)
Here are some other states in the identical
boson case:
(|1,1,0>+ |0,1,1>+|1,0,1>)/
(|2,0,0>+|0,2,0>+|0,0,2>)/
(|0,1,2>+|1,0,2>+|0,2,1>+|1,2,0>+|2,1,0>+|2,0,1>)/
And so on....
Identical Fermions
Here we must require that the WF be antisymmetric under the
exchange of any two (single particle) states....still a subspace of the
distinguishable particle Hilbert space … some examples;
(|0,1,2>-|1,0,2>-|0,2,1>+|1,2,0>-|2,1,0>+|2,0,1>)/
This would be the
ground state !
(|0,1,3>-|1,0,3>-|0,3,1>+|1,3,0>-|3,1,0>+ 3,0,1>)/
first excited state
(|2,1,3>-|1,2,3>-|2,3,1>+|1,3,2>-|3,1,2>+|3,2,1>)/
another state
Bosons and Fermions
Identical Bosons (con't)
Here are some other states in the identical
boson case:
(|1,1,0>+ |0,1,1>+|1,0,1>)/
(|2,0,0>+|0,2,0>+|0,0,2>)/
(|0,1,2>+|1,0,2>+|0,2,1>+|1,2,0>+|2,1,0>+|2,0,1>)/
And so on....
Identical Fermions
Here we must require that the WF be antisymmetric under the
exchange of any two (single particle) states....still a subspace of the
distinguishable particle Hilbert space … some examples;
(|0,1,2>-|1,0,2>-|0,2,1>+|1,2,0>-|2,1,0>+|2,0,1>)/
(|0,1,3>-|1,0,3>-|0,3,1>+|1,3,0>-|3,1,0>+ 3,0,1>)/
first excited state
(|2,1,3>-|1,2,3>-|2,3,1>+|1,3,2>-|3,1,2>+|3,2,1>)/
another state
Bosons and Fermions
Identical Bosons (con't)
Here are some other states in the identical
boson case:
(|1,1,0>+ |0,1,1>+|1,0,1>)/
(|2,0,0>+|0,2,0>+|0,0,2>)/
(|0,1,2>+|1,0,2>+|0,2,1>+|1,2,0>+|2,1,0>+|2,0,1>)/
And so on....
Identical Fermions
Here we must require that the WF be antisymmetric under the
exchange of any two (single particle) states....still a subspace of the
distinguishable particle Hilbert space … some examples;
(|0,1,2>-|1,0,2>-|0,2,1>+|1,2,0>-|2,1,0>+|2,0,1>)/
(|0,1,3>-|1,0,3>-|0,3,1>+|1,3,0>-|3,1,0>+ 3,0,1>)/
(|2,1,3>-|1,2,3>-|2,3,1>+|1,3,2>-|3,1,2>+|3,2,1>)/
another state
Fermions
That concludes our discussion of the case with three particle in the 1-d HO
potential. We can however synthesize the fermionic example which in terms
of the one-particle states will always be made from exactly 3! = 6 products of
represent the 1-particle
single particle states into a general statement. Let
states in a N-identical fermion system, interacting or not. The hilbert space of
the fermionic system is then spanned by the “Slater Wavefunctions”
=
This is identical to what we constructed by hand in the preceeding N=2 and
N=3 cases. Note that the exchange antisymmetry is guaranteed by the
properties of the determinant.
Entanglement and the Mystery of the Quantum Cakes
Read: P. Kwait and L. Hardy, Am. J. of Physics, 68 Pg. 33 (2000)
Read and discuss together in class....This is a very clear exposition
of the novelty of entanglement in quantum mechanics, which indicates
that there are quantum systems with correlations in them that cannot
be thought of in terms of any type of joint classical probability function.
Enjoy!