* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download AP Chapter 5
Eigenstate thermalization hypothesis wikipedia , lookup
Bremsstrahlung wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Nuclear structure wikipedia , lookup
Old quantum theory wikipedia , lookup
Atomic nucleus wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Electron scattering wikipedia , lookup
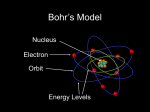
AP Chapter 5 Structure of the Atom Review Quiz Chapter 5 • Net Ionic Equations John Dalton (1766 – 1844) • Proposed the first scientifically supported atomic theory. Dalton’s Model of the Atom • Dalton's model was that the atoms were tiny, indivisible, indestructible particles and that each one had a certain mass, size, and chemical behavior that was determined by what kind of element they were. • What made us change Dalton’s Atomic Model? J. J. Thomson (1856 – 1940) • Credited for the discovery of the electron. • Invented the mass spectrometer which led to his discovery of isotopes. Scientific Inquiry • Scientists use experimental results to test scientific models, such as the model of the atom. • When experimental results are not consistent with the predictions of a scientific model, the model must be revised or replaced. Lord Ernest Rutherford (1871 – 1937) • Discovered the nucleus of the atom. Rutherford’s Gold Foil Experiment Rutherford’s Gold Foil Experiment Rutherford’s Atomic Model The “Planetary Model” of the Atom • The nucleus is very small, dense, and positively charged. • Electrons surround the nucleus. • Most of the atom is empty space Subatomic Particles PARTICLE SYMBOL CHARGE MASS (amu) LOCATION electron e- -1 0 orbit nucleus proton p+ +1 1 inside nucleus neutron n0 0 1 inside nucleus Niels Bohr • In 1913 Bohr published a theory about the structure of the atom based on an earlier theory of Rutherford's. • Bohr expanded upon this theory by proposing that electrons travel only in certain successively larger orbits. Bohr Model of the Atom The Bohr Atom • Electrons orbit the nucleus in orbits that represent specific quantities of energy. • The energies of the electrons in the atom are quantized. • Only certain electron orbits (energy levels) are allowed. Electromagnetic Waves • Properties of waves include speed, frequency, wavelength and energy • All electromagnetic waves including light travel at a speed of 3 x 108 m/s. • However the frequency, wavelength and energy of the waves vary. Wavelength () Measured in units of length: m, nm, Aº Frequency () Measured in cycles/second = hertz (Hz) Visible Light Electromagnetic Radiation • For all waves • = c c = the speed of light = 3.00 x 10 8 m/s A photon of red light has a wavelength of 665 nm. What is the frequency of this light? • • • • • 665 nm = 665 x 10-9 m c=• = c ÷ = 3.00 x 108 m/s ÷ 665 x 10-9 m = 4.511278 x 1014/s or Hz = 4.51 x 1014/s or Hz An x-ray has a frequency of 7.25 x 1020 Hz. What is the wavelength? • • • • • 7.25 x 1020 Hz = 7.25 x 1020/s c=• = c ÷ = 3.00 x 108 m/s ÷ 7.25 x 1020/s = 4.137931 x 10-13 m = 4.14 x 10-13 m Energy of Electromagnetic Radiation • For all waves: h = 6.63 x 10 E = h• -34 J • s or J/Hz A photon of red light has a wavelength of 665 nm. What is the energy of this light? A photon of red light has a wavelength of 665 nm. What is the energy of this light? • • • • • 665 nm = 665 x 10-9 m c=• = c ÷ = 3.00 x 108 m/s ÷ 665 x 10-9 m = 4.511278 x 1014/s or Hz = 4.51 x 1014/s or Hz A photon of red light has a wavelength of 665 nm. What is the energy of this light? • • • • • • • 665 nm = 665 x 10-9 m c=• = c ÷ = 3.00 x 108 m/s ÷ 665 x 10-9 m = 4.511278 x 1014/s or Hz = 4.51 x 1014/s or Hz E = h • = (6.63 x 10-34 J • s)(4.51 x 1014/s) E = 2.99013 x 10-19 J A photon of red light has a wavelength of 665 nm. What is the energy of this light? • • • • • • • 665 nm = 665 x 10-9 m c=• = c ÷ = 3.00 x 108 m/s ÷ 665 x 10-9 m = 4.511278 x 1014/s or Hz = 4.51 x 1014/s or Hz E = h • = (6.63 x 10-34 J • s)(4.51 x 1014/s) E = 2.99013 x 10-19 J = 2.99 x 10-19 J An x-ray has a frequency of 7.25 x 1020 Hz. What is it’s energy? An x-ray has a frequency of 7.25 x 1020 Hz. What is it’s energy? • E = h • = (6.63 x 10-34 J/Hz)(7.25 x 1020Hz) • E = 4.80675 x 10-13 J • E = 4.81 x 10-13 J wavelength, frequency and energy Red Light X-ray • = 665 x 10-9 m • = 4.51 x 1014 Hz • E = 2.99 x 10-19 J • = 4.14 x 10-13 m • = 7.25 x 1020 Hz • E = 4.81 x 10-13 J Wavelength, frequency and energy • Wavelength and frequency have an indirect relationship. • Energy and frequency have a direct relationship. • Electromagnetic radiation of short wavelength will have high frequency and high energy. • Electromagnetic radiation of long wavelength will have low frequency and low energy. Niels Bohr • Bohr also described the way atoms emit radiation by suggesting that when an electron jumps from an outer orbit to an inner one, that it emits light. Bohr Model Slide 9 • Electrons move around the nucleus in orbits of definite energies. • The energy of the orbit is related to its distance from the nucleus. The lowest energy is found in the orbit closest to the nucleus. • Radiation is absorbed or emitted when an electron moves from one orbit to Fig. 10-6, p. 269 another. Bohr Model of the Atom • The Bohr atom The Bohr Atom • Electrons orbit the nucleus in orbits that represent specific quantities of energy. • Electrons closer to the nucleus have less energy. Ground State • The lowest energy state of an atom. Excited State • Any energy state of an atom that is of higher in energy than the ground state. Energy Absorbed Absorption (Dark – Line) Spectra Energy Emitted Electron jumps to a lower orbit Emission (Bright – Line) Spectra Emission Spectra The lines present in an emission spectrum are the lines missing in an absorption spectrum. The Heisenberg Uncertainty Principle The Uncertainty principle • Heisenberg determined that it was impossible to experimentally determine both the position and the speed of the electron at the same time. • This became known as the Heisenberg Uncertainty Principle. • It simply means that the electron is so small and moving so fast, that the simple act of trying to measure its speed or position would change either quantity. Problems with the Bohr Model • It violates the Heisenberg Uncertainty Principle because it considers electrons to have known orbits. • It makes poor predictions regarding the spectra of atoms larger than hydrogen. Schrodinger • The Austrian scientist, Erwin Schrödinger, pursued the of the electron having wave properties and it seemed to him that the electron might be like a standing wave around the nucleus. Schrodinger’s Model • This idea agreed very well with Bohr's idea of quantized energy levels: only certain energies and therefore, wavelengths would be allowed in the atom. • This explained why only certain colors (wavelengths) were seen in the spectrum of the hydrogen atom. Schrodinger’s Model • Schrodinger set out to make a mathematical model that assumed the electron was a standing wave around the nucleus. • His solutions to that model agreed not only with the experimental evidence for hydrogen (as Bohr’s did too), but gave excellent results for all atoms when compared to their actual spectrum. Quantum Mechanics: The Structure of Atoms Schrodinger’s Model • This is our modern model of the atom and is known as the Quantum Mechanical Model. • Calculations involving the QM model of the atom can be approximated using computers. • The solutions to these calculations is the basis for modern software that calculates the structure and reactivity of molecules. The Quantum Mechanical Model The Quantum Mechanical Model • The quantum mechanical model is based on quantum theory, which says matter also has properties associated with waves. The Quantum Mechanical Model • According to quantum theory, it’s impossible to know the exact position and momentum of an electron at the same time. This is known as the Uncertainty Principle. The Quantum Mechanical Model • The quantum mechanical model of the atom uses complex shapes of orbitals (sometimes called electron clouds), volumes of space where an electron is likely to be found. The Quantum Mechanical Model • Therefore the quantum mechanical model is based on probability rather than certainty. Absorption and Emission of Energy by Molecules • A photon is a particle representing a specific amount of electromagnetic energy. • When a photon is absorbed by a molecule, the energy of the molecule is increased. • When a photon is released by a molecule, the energy of the molecule is decreased. Absorption and Emission of Energy by Molecules • Different types of molecular motion lead to absorption or emission of photons in different spectral regions. Absorption and Emission of Energy by Molecules • Ultraviolet and visible radiation is associated with electron transitions between energy levels and so can be used to study electronic structure. • This is the same as atomic spectroscopy. • Molecules however have bonds which allow for different types of absorption and emission. Absorption and Emission of Energy by Molecules • Infrared radiation is associated with molecular vibrations and so can be used to detect the type of bonds present within the molecule. Absorption and Emission of Energy by Molecules • Infrared radiation is associated with molecular vibrations and so can be used to detect the type of bonds present within the molecule. Absorption and Emission of Energy by Molecules • The microwave region of the spectrum is used for rotational spectroscopy. World of Chemistry: Molecular Fingerprints • ..\..\..\Videos\World of Chemistry\Molecular Fingerprints.mpg Energy Levels – Sublevels - Orbitals • Electrons in an atom are within atomic orbitals which are within sublevels which are within energy levels. Electron Configuration 7 4d 7 electrons are in the d sublevel in the 4th energy level SUBLEVEL s NUMBER OF ORBITALS 1 MAX. # OF ELECTRONS 2 p 3 6 d 5 10 f 7 14 Arrow Diagram 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p 5d 5f 6s 6p 6d 7s 7p Write the electron configuration for lead (Z = 82). The periodic table and electron configuration. Periodic Table and Electron Configuration s p 1 2 d (period-1) 3 4 5 6 7 6 7 6 7 f (period-2) © 1998 by Harcourt Brace & Company C. Periodic Patterns • Example - Germanium 1 2 3 4 5 6 7 [Ar] 2 10 4s 3d 2 4p Write the abbreviated electron configuration for lead (Z = 82) using the periodic table. O 6 7 © 1998 by Harcourt Brace & Company A. General Rules • Pauli Exclusion Principle – Each orbital can hold TWO electrons with opposite spins. A. General Rules • Hund’s Rule – Within a sublevel, place one e- per orbital before pairing them. – All electrons in singly filled orbitals have the same direction of spin. Incorrect Correct Orbital Filling Diagrams B. Notation • Orbital Diagram O 8e- 1s 2s • Electron Configuration 2 2 4 1s 2s 2p 2p Magnetism • Magnetism can be a complicated concept. • We will only deal with magnetism as it is predicted by electron spin which is an oversimplified way of dealing with this subject. Electron Spin & Magnetism • Opposite spins produce opposite magnetic fields. Electron Spin & Magnetism • Most materials with one or more unpaired electrons are at least slightly magnetic. These substances are said to be paramagnetic. • The overall magnetic field strength of atoms with all paired electrons is zero. These substances are said to be diamagnetic. Molecular Orbital Diagrams • One of the reasons that magnetism can be complicated is that often times the bonding within atoms creates situations where multiple atoms bond together creating molecular orbitals which greatly complicates the ability to predict the pairing of electrons. Molecular Orbitals • A molecular orbital is an orbital within a molecule whereas an atomic orbital is an orbital within an individual atom. • Both types of orbitals can hold no more than a pair of electrons. • We can draw a molecular orbital diagram to help explain the magnetic character of some simple diatomic molecules. Molecular Orbitals Diagrams See the blank MO diagram in your notebook. Molecular Orbitals Diagram for H2 Molecular Orbitals Diagram for C2 MO Diagrams Can Be Complicated . 1. Write the molecular orbital diagrams for O2 and F2. 2. Classify each substance as paramagnetic or diamagnetic. 3. Which substance will be attracted to a magnetic field? Explain. Paramagnetism of O2 ..\..\..\Videos\Paramagnetism of Liquid Oxygen.wmv Photoelectric Effect • The photoelectric effect is the emission of electrons from substances that are exposed to light. • Ionization energy is the amount of energy it takes to remove an electron from an atom. Photoelectric Effect • More energy is required to remove successive electrons from atoms. • This is due to Coulomb’s Law. Coulomb’s Law • Coulomb’s Law quantifies the general rule of electrostatics that opposites charges attract and like charges repel. • The electrostatic force between two charged bodies is proportional to the product of the amount of charge on the bodies divided by the square of the distance between them. Coulomb’s Law F= force of attraction or repulsion k = constant q1 and q2 = the charges of the two bodies r = radius between the charges Coulomb’s Law • If the bodies are oppositely charged, one positive and one negative, they are attracted toward one another; if the bodies are similarly charged, both positive or both negative, the force between them is repulsive. Coulomb’s Law Coulomb's law helps describe the forces that bind electrons to an atomic nucleus. • Based on Coulomb’s Law, the force between two charged particles is proportional to the magnitude of each of the two charges and inversely proportional to the square of the distance (radius) between them. Photoelectric Effect • Light consists of photons of a certain energy (E = h • ). • In the photoelectric effect, light ejects electrons from a material. This requires the photon to have sufficient energy to eject the electron. • This is known as Photoelectron Spectroscopy (PES) Photoelectron Spectroscopy (PES) • Photoelectron Spectroscopy (PES) determines the energy needed to eject electrons from a substance. Photoelectron Spectroscopy (PES) • Photoelectron Spectroscopy (PES) supports the shell, subshell model of the atom. • PES data for multielectron atoms show that certain electrons have ionization energies that are relatively close to one another. We therefore group these electrons into shells and subshells as a result. Photoelectron Spectroscopy (PES) • Photoelectron Spectroscopy (PES) data for atoms also helps us to confirm the number of electrons within particular shells and subshells. • The intensity of the photoelectron signal at a given energy is a measure of the number of electrons in that shell or subshell. All the previous PES slides all come from this website • http://www.chem.arizona.edu/chemt/Flash/ photoelectron.html Spectrophotometer Lab: Preparing and Diluting Solutions Spectrophotometer Lab: Preparing and Diluting Solutions