Download No Slide Title

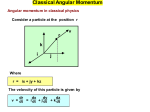
Lecture 14: Angular Momentum-II.
The material in this lecture covers the following in Atkins.
Rotational Motion
Section 12.7 Rotation in three dimensions
Lecture on-line
Angular Momentum-II (3- D) (PDF)
Angular Momentum-II (3-D) (PowerPoint)
Handout for this lecture (PDF)
Tutorials on-line
Vector concepts
Basic Vectors
More Vectors (PowerPoint)
More Vectors (PDF)
Basic concepts
Observables are Operators - Postulates of
Quantum Mechanics
Expectation Values - More Postulates
Forming Operators
Hermitian Operators
Dirac Notation Use of Matricies
Basic math background
Differential Equations
Operator Algebra
Eigenvalue Equations
Extensive account of Operators
Extensive account of Operators
Audio-visuals on-line
Rigid Rotor (PowerPoint)
(Good account from the Wilson Group,****)
Rigid Rotor (PDF)(Good account from the
Wilson Group,****)
Slides from the text book
(From the CD included in Atkins ,**)
Classical Angular Momentum
Angular momentum in classical physics
Consider a particle at the position r
Review of classical physics
Position and velocity in 3D
v
r
k
i
j
Where
r = ix + jy + kz
The velocity of this particle is given by
dr
dx
dy
dz
v = dt = i dt + j dt + k dt
Classical Angular Momentum
The linear momentum of the particle with mass m is
given by
dx
p = mv where e.i px = mvx = m dt
The angular momentum is defined as
Review of classical physics
Angular Momentum in 3D
L = rXp
L
|r| |p| sin

p

r
L =rXp
The angular momentum is perpendicular to the plane
defined by r and p.
Classical Angular Momentum
Review of classical physics
We have in addition
Angular Momentum in 3D
L = rXp = (ix +jy + kz)X (ipx + jpy +kpz)
L = (r ypz -rzpy)i + (rzpx -rxpz)j + (rxpy - rypx)k
or
i
rXp =
rx
px
j
k
ry
rz
py
pz
Classical Angular Momentum
Why are we interested in the angular
momentum
Review of classical physics
?
Angular Momentum in 3D
Consider the change of L with time
F
dL
dr
dp
dt = dt Xp + rX dt
dL
dp
dt = mvXv + rX dt
r
dp
= rX dt
dL
d
dr
d2 r
dt = rX dt [m dt ] = rXm dt 2
m
d2r
dt 2
 F (Newtons Law)
Classical Angular Momentum
Review of classical physics
Angular momentum and
central force in 3D
dL
 r F
dt
F
r
For centro-symmetric systems in which
the force works in the same direction as r
we must have
dL
dt = 0 : THE ANGULAR
MOMENTUM IS CONSERVED
Classical Angular Momentum
Review of classical physics
Angular momentum and
r
Examples :
F central force in 3D
movement of electron around nuclei
movement of planets around sun
For such systems L is a constant of motion, e.g. does
not change with time since
dL
dt = 0
In quantum mechanics an operator O representing a
constant of motion will commute with the Hamiltonian
which means that we can find eigenfunctions that are
both eigenfunctions to H and O
Quantum mechanical representation of angular momentum
operator
Rotation..Quantum Mechanics 3D
We have
L = rXp = iLx + jLy + kLz
where
Angular momentum operators
of quantum mechanics
in 3D
Lx = ry pz - rzpy ; Ly = rzpx - rx py ; Lz = rx py - ry px
In going to quantum mechanics we have
x --> x
; y --> y ; z --> z

px --> -i x


; py --> -i y ; pz --> -i z
Thus :




Lx = -i (y z - zy ) ; Ly = -i (z x - xz )


L z = -i (x y - yx )
Rotation..Quantum Mechanics 3D
We have
Angular momentum operators
of quantum mechanics
in 3D
L = iLx + jLy + kLz
thus
L.L = L 2 =(iLx + jLy + kLz).(iLx + jLy + kLz)
L2 = Lx 2 + Ly 2 + Lz2
Rotation..Quantum Mechanics 3D
Can we find common eigenfunctions to
L 2 , Lx , Ly , Lz
?
Commutation relations for
angular momentum operators
of quantum mechanics in 3D
Only if all four operators commute
We must now look at the commutation
relations
The two operators L1 and L2 will
commute if
[L1,L2 ] f(x,y,z) =(L1L2 - L2L1) f(x,y,z) = 0
Rotation..Quantum Mechanics 3D Commutation relations for
angular momentum operators
of quantum mechanics in 3D
ˆ2  L
ˆ L
ˆ representing
For the quantum mechanical operators L
the square of the length of the angular momentum
as well as the operators representing the three Cartesian
ˆ x ;L
ˆ y; L
ˆz
components of the angular momentum vector L
we have
[Lˆ2 , Lˆ x ]  [Lˆ2 , Lˆ y ]  [Lˆ2 , Lˆ z ]  0
[Lˆ , Lˆ ]  i Lˆ
x
y
[Lˆ y , Lˆ z ]  i
[Lˆ , Lˆ ]  i
z
x
z
Lˆ x
Lˆ
y
Rotation..Quantum Mechanics 3D
Common eigenfunctions for
ˆ and L
ˆ2 .
L
z
How do we find the eigenfunctions ?
The eigenfunctions f must satisfy
L zf = af
and
L 2f = bf
The function f must in other words
satisfy the differential equations
L zf = af
as well as
L 2f
= bf
Rotation..Quantum Mechanics 3D
It is more convenient to solve the equations in
Angular momentum operators
spherical coordinates
(x,y,z)  (r,  

of quantum mechanics in
spherical coordinates in 3D
r

We find after some tedious but straight forward
manipulations
d
Lz = -i  ]
d
d2
d
1
d2
L 2 = - 2[
+cot  sin2
]
2

d
d
d
Rotation..Quantum
Mechanics 3D
Common eigenfunctions for
ˆ z and L
ˆ2 .
L
We must solve :
ˆ z(,)  b(,) and L
ˆ 2 (,)  c(,)
L
The eigenfunctions to L2 and Lz are given by
(,) = Yl,m ((,)
2l+ 1 (l | m!| |m|
=
Pl (cos)  exp[im]
4 (l | m!|)
Eigenfunctions are orthonormal
2 sindd   
*
Y
(,)Y
(,)
r
 lm
l'm'
l,l' m,m'
Rotation..Quantum Mechanics 3D
Common eigenfunctions for
ˆ and L
ˆ2 .
L
z
2l+ 1 (l | m!| |m|
(,) = Yl,m ((,) =
Pl (cos )  exp[im]
4 (l | m!|)
We have that l can take the values : l = 0,1, 2, 3,4..
and the possible eigenvalues for L2 are 2l(l  1)
ˆ 2  (,)  2 l(l  1) (,)
L
lm
lm
for a given l value m can take the 2l+ 1 values
- l, - l + 1,...,-1,0,1,...,l - 1,l
and the possible eigenvalues for Lz are m
ˆ z lm (,)  m lm (, )
L
Rotation..Quantum Mechanics 3D
ˆz
Common eigenfunctions for L
ˆ 2 . Spherical harmonics
and L
2l+ 1 (l | m!| |m|
(,) = Yl,m ((,) =
Pl (cos )  exp[im]
4 (l | m!|)
l
m
0
0
1
1
0
1
Y lm (,)
1
4
3
cos
4
3
sin exp[i]
4
Rotation..Quantum Mechanics 3D
ˆz
Common eigenfunctions for L
ˆ 2 . Spherical harmonics
and L
2l+ 1 (l | m!| |m|
(,) = Yl,m ((,) =
Pl (cos )  exp[im]
4 (l | m!|)
l
m
Y lm (,)
2
0
5
(3cos2  1)
16
2
1
15
cossin[i]
8
2
15
sin 2 exp[2i]
32
2
ˆz
Common eigenfunctions for L
ˆ 2 . Spherical harmonics
and L
2l+ 1 (l | m!| |m|
(,) = Yl,m ((,) =
Pl (cos )  exp[im]
4 (l | m!|)
Rotation..Quantum
Mechanics 3D
l
3
3
3
3
m
Y lm (,)
0
7
(5cos3  3 cos)
16
1
21
(5cos 2  1)sin [i]
64
2
105
sin2  cos exp[2i]
32
3
35
sin3  exp[2i]
64
What you should learn from this lecture
1. you should know the definition of angular
momentum as L = rxp.
2. You should be aware of the commutation relations
[Lˆ2 , Lˆ ]  [Lˆ2 , Lˆ ]  [Lˆ2 , Lˆ ]  0
x
y
z
[Lˆ x , Lˆ y ]  i Lˆ z ;[Lˆ y , Lˆ z ]  i Lˆ x;[Lˆ z , Lˆ x ]  i Lˆ y
3. You should realize that the above commutation
has the consequence that we only can find
ˆ 2 and one of the
find common eigenfunctions to L
ˆ . Thus we can
components , normally taken as L
z
only know L2 and Lz precisely.
What you should learn from this lecture
4. You are not required to know the exact form of the
eigenfunctions
2l+ 1 (l | m!| |m|
(,) = Yl,m ((,) =
Pl (cos )  exp[im]
4 (l | m!|)
ˆ z and L
ˆ2
to L
5. You should know that l can take the values : l = 0,1, 2, 3,4..
and the possible eigenvalues for L2 are 2l(l  1)
ˆ 2  (,)  2 l(l  1) (,)
L
lm
lm
6. You should know that
for a given l value m can take the 2l+ 1 values
- l, - l + 1,...,-1,0,1,...,l - 1,l
and the possible eigenvalues for Lz are m
ˆ z lm (,)  m lm (, )
L
We have
Appendix : Commutator relations for
angular momentum components Lx ;L y ;Lz ;L2 .
f
f
Lxf = -i ( yz - zy ) = -i u x
f
f
L yf = -i ( zx - xz ) = -i u y
Next
LxLyf = -i Lxu y
u y
u y
LxLyf = -i [ -i ( y z - z y ) ]
u y
u y
LxLyf = - 2 [ y z - z y ]
Appendix : Commutator relations for
angular momentum components Lx ;L y ;Lz ;L2 .
We have
uy
 f f
z = z (zx - xz )
uy
f
2f
2f
z = x + zzx - xz
Further
uy  f f
= y (zx - xz )
y
uy
y =
2f
2f
z yx - x yz
combining terms
Thus
Appendix : Commutator relations for
angular momentum components Lx ;L y ;Lz ;L2 .
f
2f
2f
2f
2f
LxLyf = - 2[ yx + yzzx - yxz - z2yx +zxyz ]
f
2f
2f
2f
2f
LxLyf = - 2[ yx + yzzx - yxz - z2yx +zxyz ]
It is clear that L xLyf can be evaluated by
interchanging x and y We get:
f
2f
2f
2f
2f
LyLxf = - 2[ xy + xzzy - xyz - z2xy +zyxz ]
Appendix : Commutator relations for
angular momentum components Lx ;L y ;Lz ;L2
using the relations
2f
2f
zy = yz
etc.
We have
f
f


[ LxLy - LyLx] f = - 2[ yx - xy ] = - 2[ yx - xy ]
f


We have: L z = -i [ x y - yx
Thus: [ LxLy - LyLx] f
]
= i Lz f ; [Lx,Ly] = i Lz
We have shown [L x,Ly] = i Lz
Appendix : Commutator relations for
angular momentum components Lx ;L y ;Lz ;L2 .
By a cyclic permutation
Z
X
C3
z
Y
Y
z
X
X
Y
[ Ly,L z] = i Lx
[ Lz,Lx ] = i Ly
We have shown that the three operators L x ,L y ,L z
are non commuting
What about the commutation between L x ,Ly ,Lz and L2
Appendix : Commutator relations for
angular momentum components Lx ;L y ;Lz ;L2 .
Let us examine the commutation relation
between L2 and L x
We have :
[ L2 ,L x ]  [L2x  L2y  L2z ,L x ]
[ L2 ,L x ]  [L2x ,L x ]  [L2y ,Lx ]  [L2z ,Lx ]
For the first term
[L2x ,L x ]  L2xL x  L xL2x  L3x  L3x  0
Appendix : Commutator relations for
angular momentum components Lx ;L y ;Lz ;L2 .
For the second term
[L2y ,L x ]  L2yLx  LxL2y
2
2
 L yLx  LyL xLy  L yLxL y  L xLy
 L y [L yL x  L xL y ]  [L yLx  LxL y ]L y
Z
 i LyL z  i LzL y
X
Y
Appendix : Commutator relations for
angular momentum components Lx ;L y ;Lz ;L2 .
For the third term
[L2z,Lx ]  L2zL x  L xL2z
2
2
 L zL x  LzLxL z  LzL xLz  L xLz
 L z[LzL x L xLz ]  [LzL x  L xLz ]L z
 i L zL y  LyL z
Z
X
Y
Appendix : Commutator relations for
angular momentum components Lx ;L y ;Lz ;L2 .
In total
[ L2 ,L x ]  [L2x  L2y  L2z ,L x ]
0
i L yLz  i LzLy i L zL y  LyL z
Z
X
Y
0
Appendix : Commutator relations for
angular momentum components Lx ;L y ;Lz ;L2 .
We have shown
[L2,Lx] = [L x 2+Ly 2+Lz2,Lx ] = O
now by cyclic permutation
Z
X
Y
[Ly 2+Lz2+Lx 2,Ly ] = [L2,Ly ] = 0
[Lz2+Lx 2+Ly 2,Lz] = [L2,Lz] = 0
Thus Lx ,Ly ,Lz all commutes with L 2
and we can find common
L2 and Lx
or L 2 and Ly
eigenfunctions for
or L 2 and Lz
the normal convention is to obtain eigenfunctions that are
at the same time eigenfunctions to L z and L2.
How do we find the eigenfunctions ?
Rotation..Quantum Mechanics 3D
We have

-i  S()T() = b S()T()
or

-i S() T()= b S()T()
multiplying with 1/ S( ) from left
T()

=
ib
T()
The general solution is
T() = AExp[
ib
]
A general point in 3-D space is given by
( r,)
Z
rcos
(x,y,z)  (r,  

r

Y
X
rsin 
We have the following relation
x= r sincos
y= r sinsin
z= r cos
The same point is represented by (r, +2)
We must thus have
ib
ib
ib
ib
Exp[ ] = Exp[ (  2) = Exp[ ] Exp[ 2]
Thus
Exp[
ib
2b 
2b 
2] = cos
+ isin
=1




This equation is only satisfied if
b
= m
with
m = 0,±1,±2,......
Thus the eigenvalue b is quantized as
b =
m
m = 0,±1,±2,......
The possible eigenfunctions are
T() = AExp[im] , m = 0,±1,±2,......