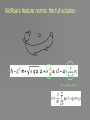* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Potts Networks – Latching – Correlated patterns
Artificial intelligence for video surveillance wikipedia , lookup
Artificial neural network wikipedia , lookup
Binding problem wikipedia , lookup
Nervous system network models wikipedia , lookup
Feature detection (nervous system) wikipedia , lookup
Neuroeconomics wikipedia , lookup
Convolutional neural network wikipedia , lookup
Reconstructive memory wikipedia , lookup
Metastability in the brain wikipedia , lookup
Central pattern generator wikipedia , lookup
Catastrophic interference wikipedia , lookup
Recurrent neural network wikipedia , lookup
Types of artificial neural networks wikipedia , lookup
Statistical and dynamical properties of large cortical network models: insights into semantic memory and language Emilio Kropff Thesis presentation September 19, 2007 Potts Networks – Latching – Correlated patterns Cerebral cortex – Braitenberg & Schüz, 1991 # of neurons >> # of input fibers Modifiable synapses No prefered direction in the connections Mostly excitatory synapses Two-level associative memory with formation of cell assemblies Great convergence & divergence Connections are very weak Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Auto-associative memories - No activity - Pattern #1 active - Pattern #2 active - Pattern #3 active Emilio Kropff, LIMBO-CNS-SISSA Hebbian Learning !! Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Testing the memory - Pattern #2 active Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Testing the memory Emilio Kropff, LIMBO-CNS-SISSA Network damage Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Two-level associative memory with formation of cell assemblies • Anatomical studies – Braitenberg & Schüz • Embodied theories of semantic memory • Feature representation Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns The model: the trick • S: number of alternative states of of a unit features a unit • a (global sparseness): average number of units that are active in a global features describing a memory concept state 1 state 2 state 0 … state S Emilio Kropff, LIMBO-CNS-SISSA state 3 Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Testing Kanter’s Potts network (Kanter,1988) J kl ij p 1 NS 2 ( S 1 i k N s h J ijkl ( S j l 1) 1)( S l 1) k i j j 1 l 0 • The patterns ξ are constructed randomly and stored in the network by modifying J. • The state of the network is set to some initial value (e.g: random or some stored memory if we want to test its stability). • A unit i is picked randomly and the fields hik are calculated. • The S states of unit i are updated following: i arg max (hik ) k k i exp( hik ) S exp( h ) l 0 Emilio Kropff, LIMBO-CNS-SISSA l i Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Reviewing and extending the results of Kanter, 1988 • Kanter’s result for low S is p N pmax S (S 1) • We find high S behaviour is 2 pmax max S ( S 1) erf( 2 ) S ( S 1) log(2 ) 1 2 S)2 erf (1 S 1 ) log( Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Adding a zero state and sparseness a h mv qPk S (1 a~ )(1 a~C ) 2 zk vk (1 0 )( U 2 S 2(aC ) 1 aˆC ) k Sparse Hopfield (Buhmann, 1989, Tsodyks, 1988) αc ~ 1/a Emilio Kropff, LIMBO-CNS-SISSA Potts without sparseness (Kanter, 1988) ~ 0.14 S(S-1) Sparse Potts (Kropff & Treves, 2005) S2/a Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Highly diluted approximation h mv qPk S (1 a~ )(1 a~C ) 2 zk vk (1 0 )( U 2 S 2(aC ) 1 aˆC ) k • Two units speak to each other with probability cM/N • Two states speak to each other with probability e 0.08 z k vk (1 0 )( U ) 0.05 Normalized storage capacity - ca/S 0.07 2 Normalized storage capacity - ca/S eff qPk highly diluted S (1 a~ ) fully connected 2 h mv k 0.06 0.05 0.04 0.03 0.02 0.01 0.00 eff c p e highly diluted fully connected M 0.04 0.03 0.02 0.01 0.00 1E-5 1E-4 1E-3 0.01 sparseness - a Emilio Kropff, LIMBO-CNS-SISSA 0.1 1 10 100 1000 10000 100000 Number of states in a unit - S Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns 1 4 Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 • The Kanter result for Potts networks has a logarithmic correction for high S. • If well defined, a sparse Potts network reaches an S2 optimal storage capacity c 4 a log( S ) a •In highly diluted networks this result applies, with = p/(cM e) . •These results are in line with the conjecture of a limit in the amount of information per synapse that a network can store. Potts Networks – Latching – Correlated patterns latching! Overlaps between the state and the patterns retrieval + adaptation + correlation Overall activity Dynamics of the network 5 4 3 2 1 1 0.8 0.6 0.4 0.2 0 100 Emilio Kropff, LIMBO-CNS-SISSA 200 300 Timetime cycles 400 Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns • In addition, the transition matrix is not symmetric • • Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Dynamics: latching of 2 patterns Overlaps between the state and the patterns 1 0.8 0.6 0.4 0.2 0 time Emilio Kropff, LIMBO-CNS-SISSA 200 400 Time cycles 600 800 Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns 100 1 Dynamics: latching of 2 patterns 80 1 60 0.8 0.8 ‘alternative features’ 0.6 •Units active in both patterns in different 0.4 states 0.6 40 0.4 0.2 0.2 20 100 200 300 400 500 600 • Units active in one of the two patterns 1 -0.2 0 0 100 0.8 0 20 40 60 80 First Pattern M aximum at t1 100 • Unitsactive in both in the same state 0.6 0.4 100 0.2 1 ‘pathological case’ c: shared units 100 100 200 300 400 500 600 -0.2 80 0.8 60 0.6 • Weakly: units active in both patternsin different states 1 0.4 40 ‘shared features’ 0.8 0.6 0.2 20 0.4 • Units active in one of the two patterns 0.2 0 0 100 0 20 40 60 80 First Pattern M aximum at t1 200 300 400 500 600 • Unitactive in both in the same state 100 -0.2 d: shared features Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Does latching present a natural rudimentary grammar? Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 • Correlation seems to be at least one of the main properties determining latching. • However, the transition matrix is not symmetric, which means that there are other important factors. • The equilibrium between global inhibition and local self excitation can control the complexity of symbolic chains. • Three types of latching transition exist, each in a restricted region of parameters. Do they organize in time? Potts Networks – Latching – Correlated patterns Category specific deficits • Patients were found with a significant impairment in their knowledge about living things (animals + foodstuffs) as opposed to manmade artifacts (Warrington & Shallice, 1984). • Impairment for nonliving has also been reported → double dissociation. Current ratio: 23% vs 77% (Capitani, 03) Theoretical accounts • The selective impairments respond to differences in the networks representing different categories: sensory/functional theory (Warrington & Shallice, 84), domain-specific hypothesis (Caramazza & Shelton, 98). • The network sustaining semantic memory is quite homogeneous but different categories have different typical correlation properties (McRee et al, 97; Tyler & Moss, 01; Sartori & Lombardi, 04). Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Hopfield memories • If patterns are randomly correlated (Tsodyks,88), • However, if patterns have a non-trivial structure of correlations, the storage capacity colapses. • Solution #1: Orthogonalize the patterns before feeding the network. (i.e: Dentate Gyrus in Hippocampus) • In semantic memory correlation between stored patterns seems to play a major role. Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Solution #2 ?? • We assume that pattern 1 is being retrieved • We split hi into the contribution of pattern 1 (signal) and the rest (noise) • We minimize the noise Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Classical result: hebbian learning supports uncorrelated memories Classical result: catastrophe associated to correlated memories Jij= Σμ (ξiμ – a ).(ξjμ – a ) Jij= Σμ (ξiμ - ai).(ξjμ - aj) popularity: ak= 1/p Σμ ξkμ New result: a modification that supports correlated memories New result: the performance is the same with uncorrelated memories Potts Networks – Latching – Correlated patterns Propeties with finite α, C ≈ ln(N) GAUSSIAN noise (If there is independence between neurons i and j). Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Propeties with finite α, C ≈ ln(N) GAUSSIAN noise (If there is independence between neurons i and j). Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Propeties with finite α, C ≈ ln(N) F(x) ... (uncorrelated patterns) If F(x) decays fast enough Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Propeties with finite α, C ≈ ln(N) F(x) If F(x) decays exponentially If F(x) decays fast enough Emilio Kropff, LIMBO-CNS-SISSA If F(x) decays as a power law Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns pmax c C p c C min Emilio Kropff, LIMBO-CNS-SISSA Storing memories Damaging the network Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Storage capacity ~ fixed p 1 70 60 Performance Number of neurons Connectivity 1 c 1 aS f 50 40 30 20 10 0 0.2 0.4 Popularity ai Cc1 C Cc Cc2 (# of afferent connections per neuron) Entropy Sf= Σi ai (1-ai) summed over active neurons in the pattern Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Category specific effects McRae feature norms non living Probability Distribution • 541 concepts described in terms of 2526 features living • i=1 if feature i is included in the description of concept and i =0 otherwise Entropy Sf of objects Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 • When memories are correlated, they have variable degrees of ressistance to damage. • The robustness of a memory is inverse to how informative it is (Sf). • In addition, popular neurons affect negatively the general performance (decay of F(x)). • These results show how the current trend in category specific deficits (‘living’ weaker than ‘non living’) could emerge even in a purely homogeneous network. • A singel cortical network with Potts units including addaptation and storing correlated patterns of activity in its long range synapses, presents all the properties studied in this thesis. Thank you! McRae’s feature norms # of features • In the semantic memory literature, auto-associative networks are often presented as weak models. Why? popularity • To convince psychologists one must show an autoassociative memory that is able to store feature norms. Performance of the network McRae’s feature norms Size of the subgroup of patterns If – average information a – average sparseness McRae’s feature norms Number of patterns p in the subgroup Performance of the network McRae’s feature norms Size of the subgroup of patterns McRae’s feature norms Why the real network performs poorly? • Independence between features is not valid (e.g: beak and wings). Is this effect strong enough? In case it is, there would be a storage capacity colapse. • The system works but the approximation of diluted connectivity is not good. McRae’s feature norms: the full solution + 2+ 3+ ... Performance of the network McRae’s feature norms: the full solution Size of the subgroup of patterns McRae’s feature norms: strategies to store more patterns % of patterns retrieved 1- add unpopular neurons 2- eliminate popular neurons 100 100 80 80 60 60 40 40 20 20 a 0 3000 4000 5000 6000 b 2490 2500 Total number of neurons 2510 2520 McRae’s feature norms: strategies to store more patterns 3- recombination neurons i and j have high popularity: their coincidence will be less popular. If applied massively, this principle could change the whole distribution. 4- popularity deppendent connectivity The (episodic) memory pyramid popularity calculation orthogonalization Hippocampus final storage Entorhinal cortex Perirhinal and parahippocampal cortex Unimodal and polymodal association areas Primary cortex: sensory motor areas Potts Networks – Latching – Correlated patterns Propeties with α ≈ 0, C ≈ ln(N) Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Propeties with α ≈ 0, C ≈ ln(N) ac a c Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Propeties with α ≈ 0, C ≈ ln(N) • If you want to be an attractor, you should pick at least some unpopular units. • Lowering U can make any pattern retrievable -> ATTENTION Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007 Potts Networks – Latching – Correlated patterns Dynamics: latching of 2 patterns 1 0.8 ‘alternative features’ •Units active in both patterns in different states 0.6 0.4 0.2 100 200 300 400 500 600 • Units active in one of the two patterns 1 -0.2 0.8 • Unitsactive in both in the same state 0.6 100 100 1 0.4 80 80 0.8 60 60 0.6 c: alternative features 0.2 ‘pathological case’ 100 40 200 300 400 500 600 0.4 40 -0.2 20 • Weakly: units active in both patternsin different states 0.2 20 0 0 0 0 20 40 60 80 First Pattern M aximum at t1 100 0 20 40 60 80 First Pattern M aximum at t1 100 1 100 100 80 80 ‘shared features’ 1 0.8 0.8 0.6 60 60 0.6 40 40 0.4 0.4 • Units active in one of the two patterns 0.2 20 0.2 20 100 200 300 400 500 600 • Unitactive in both in the same state 0 0 0 0 20 40 60 80 First Pattern M aximum at t1 100 -0.2 0 20 40 60 80 First Pattern M aximum at t1 100 d: shared features Emilio Kropff, LIMBO-CNS-SISSA Thesis presentation. September 19th, 2007