* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Approximate Theory of Rectangular Optical Waveguides
Dispersion staining wikipedia , lookup
Vibrational analysis with scanning probe microscopy wikipedia , lookup
Astronomical spectroscopy wikipedia , lookup
Optical aberration wikipedia , lookup
Photomultiplier wikipedia , lookup
Surface plasmon resonance microscopy wikipedia , lookup
Nonimaging optics wikipedia , lookup
Super-resolution microscopy wikipedia , lookup
Birefringence wikipedia , lookup
Anti-reflective coating wikipedia , lookup
Atmospheric optics wikipedia , lookup
Gamma spectroscopy wikipedia , lookup
Confocal microscopy wikipedia , lookup
Ellipsometry wikipedia , lookup
Optical rogue waves wikipedia , lookup
Ultraviolet–visible spectroscopy wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Optical coherence tomography wikipedia , lookup
Retroreflector wikipedia , lookup
Magnetic circular dichroism wikipedia , lookup
Optical amplifier wikipedia , lookup
Harold Hopkins (physicist) wikipedia , lookup
3D optical data storage wikipedia , lookup
Nonlinear optics wikipedia , lookup
Fiber-optic communication wikipedia , lookup
Photon scanning microscopy wikipedia , lookup
Ultrafast laser spectroscopy wikipedia , lookup
Photonic laser thruster wikipedia , lookup
Optical tweezers wikipedia , lookup
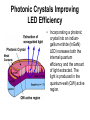
6. Optoelectronic Devices Optical Waveguides (a) A buried-in rectangular waveguide, (b) a buried-in rib waveguide, (c) a strip-loaded waveguide, and (d) a diffused waveguide Some Fabrication Processes of Optical Waveguides Basic Theory of Waveguides Theory of Planar Optical Waveguides Approximate Theory of Rectangular Optical Waveguides Surrounding by a Uniform Medium Approximate Theory of Rectangular Optical Waveguides Surrounding by a Uniform Medium (Cont’) Approximate Theory of Rectangular Optical Waveguides Surrounding by a Uniform Medium (Cont’) Applications of Y-Branches and Bends of Conventional Optical Waveguides Multimode Interference (MMI) Devices Example of Optical Performance of MMI Device 1×n MMI Optical Splitters All-optical Logic Gate Based on MMI Waveguide All-optical Logic Gate Based on MMI Waveguide (Cont’) All-optical Logic Gate Based on MMI Waveguide (Cont’) Photonic Crystals Square-lattice and Triangular-lattice Photonic Crystals Band Structures of Photonic Crystals Eg. The band structures of the 2D square-lattice photonic crystal with the lattice constant is a=0.5μm. The radius of the pillar is Rc=225nm. And the refractive index of the pillar is 3.16227766. Photonic Crystals Improving LED Efficiency • Incorporating a photonic crystal into an indiumgallium-nitride (InGaN) LED increases both the internal quantum efficiency and the amount of light extracted. The light is produced in the quantum-well (QW) active region. Photonic Crystals Improving LED Efficiency (Cont’) Far-field emission patterns from a conventional (left) and a photonic-crystal LED (right) are very different. The latter has a strongly-modified emission pattern due to the scattering of waveguided modes out of the LED chip. Photonic Crystal Waveguides (PCWGs) Comparison between the Conventional Waveguides and the PCWGs • • The conventional optical waveguides are weakly guided. There exist large power losses in the wide-angle bends/branches. However, the same structures made of line-defect photonic crystals give little losses because the lights were trapped by the defects of the photonic crystals. Most of the conventional optical waveguide devices can be easily modulated by EO effect, AO effect, and so on. But only a few photonic crystal waveguide devices can be modulated. Periodical Dielectric Waveguides (PDWGs) Electro-Optic (EO) Effect Pockels effect: Kerr effect: • The electro-optic (EO) effect is a nonlinear optical effect that results in a refractive index that is a function of the applied electric field (voltage) • Examples of Pockels effect : Ammonium dihydrogen phosphate (ADP), Potassium dihydrogen phosphate (KDP), Lithium Niobate, Lithium Tantalate, etc. • Examples of Kerr effect: Most glasses, gases, and some crystals Phase Modulators • Phase shift = , where Vπ (the halfwave voltage) is the voltage applied to achieve a phase shift of π radians. Mach-Zehnder Modulator to Modulate Amplitude of Light Output Intensity: I out V 1 cos 0 V I in 2 Consider the case of φ0=0. If V=Vπ, then Iout=Iin is the maximum, else if V=0, then Iout=0 is the minimum. Characteristics of Optical Modulators/Switches • Extinction Ratio: η=(I0-Im)/I0 if Im≦I0 and η=(ImI0)/Im if Im≧I0, where Im is the optical intensity when the maximum signal is applied to the modulator and I0 is the optical intensity with no signal applied. • Insertion Loss: Li=10log(It/Im), where It is the transmitted intensity with no modulator and Im is the transmitted intensity when the maximum signal is applied to the modulator. • Bandwith: △f=2π/T, where T is the switching time. Optical Directional Coupler as a Channel Switch A Complicated Optical Directional Coupler 3dB-Directional Coupler as a Beam Splitter Coupled-Mode Equations to Analyze Directional Coupler Coupled-Mode Equations (Cont’) • • The coupling length is Lc=π/2κ. Both Lc and κ depend on the refractive index distribution of guide. While the waveguiding mode traverses a distance of odd multiple of the coupling length (Lc, 3Lc, …, etc), the optical power is completely transferred into the other waveguide. But it is back to the original waveguide after a distance of even multiple of the coupling lengths (2Lc, 4Lc, …, etc). If the waveguiding mode traverses a distance of odd multiple of the half coupling length (Lc/2, 3Lc/2, …, etc), the optical power is equally distributed in the two guides. Acousto-Optic (AO) Modulators Bragg-type: Width >> 2/ Raman-Nath-type: Width << 2/ : wavelength of light : wavelength of acoustic wave Bragg-type AO modulator: sinθB=/2 Raman-Nath type AO modulator: sinθm=m/2, m: integer Bragg-type AO Modulator as Spectrum Analyzer Acousto-optic materials: Visible and NIR — Flint glass, TeO2, fused quartz Infrared — Ge High frequency — LiNbO3, GaP Operations of Bragg-type AO modulator: — Bragg diffraction effect — Driving frequency: 1MHz ~ 1GHz — Rise time: 150 ns (1-mm diameter laser) Bragg angle: d sin 1 2 : wavelength of light : wavelength of acoustic wave Direct Coupling from Laser/Fiber to Waveguide • Direct Coupling Efficiency: ( x, y) ( x, y)dxdy ( x, y) dxdy 2 2 ( x, y ) dxdy 2 where (x) is the laser/fiber mode and (x ) is the waveguide mode. Coupling Efficiency from Laser/Fiber to Waveguide Coupling Efficiency from Laser/Fiber to Waveguide (Cont’) Coupling Efficiency from Laser/Fiber to Waveguide (Cont’) Simulation Results Coupling Efficiency from Laser/Fiber to Waveguide For given waveguide’s fundamental mode, one can obtained the optimal coupling efficiency by selecting the values of w and c. Typical Optical Disks DVD Disks Lasers in DVD Players Optoelectronic Devices in DVD Players Band Theory of Semiconductor Devices • Metal: The conduction band and the valence band may overlap. • Semiconductor: The bandgap between the conduction band and the valence band is very small. The electron can be easily excited into the conduction band to become a free electron. • Insulator: The bandgap between the conduction band and the valence band is very large. The electron is hardly excited into the conduction band to become a free electron. Semiconductor Fermi energy level, EF: the highest energy level which an electron can occupy the valance band at 0°k Bandgap Theory of Diode Bandgap Theory of Tunnel Diode Bandgap Theory of n-p-n Transistor Radiation from a Semiconductor Junction wavelength of radiation: where : energy gap (ev) 1240 (nm) E(ev) : wavelength of radiation (nm) e.g. GaAs =1.43 ev, find the radiation wavelength 1240 876 (nm) Near Infrared (NIR) 1.43 Homojunction Laser Diode Formation of Cavity in Laser Diode Threshold Current Heterostructure Laser Diodes Stripe AlGaAs/GaAs/AlGaAs LD • Advantages of stripe geometry : 1. reduced contact area → Ith↓ 2. reduced emission area, easier coupling to optical fibers • Typical W ~ a few μm, Ith~ tens of mA • Poor lateral optical confinement of photons Buried Double Heterostructure LD • Good lateral optical confinement by lower refractive index material →stimulated emission rate ↑ • Active region confined to the waveguide defined by the refractive index variation → index guided laser diode • Buried DH with right dimensions compared with the λ of radiation → only fundamental mode can exist→ single mode laser diode • DH AlGaAs/GaAs LD • → ~ 900 nm LD • DH InGaAsP/InP LD → 1.3/1.55 μm LD Output Modes of LD • Output spectrum depends on 1. optical gain curve of the active medium 2. nature of the optical resonator • L decides longitudinal mode separation. W & H decides lateral mode separation • With sufficiently small W & H→only TEM00 lateral mode will exist ( longitudinal modes depends on L ) • Diffraction at the cavity ends →laser beam divergence ( aperture ↓→diffraction ↑) Current Dependence of Power Spectrum in LD • Output spectrum depends on 1. optical gain curve of the active medium, and 2. nature of the optical resonator • Output spectrum from an index guided LD low current →multimode high current →single mode Light Detectors Classification by spectral response wide spectral response narrow spectral response Principles of photodetection External photoelectric effect Eg. vacuum photodiode photomultiplier Internal photoelectric effect Eg. p-n junction photodiode PIN photodiode avalanche photodiode Characteristics of Light Detectors Responsivi ty : ratio of output to radiant input V I o or o I I I : applied radiant or liminous flux (W or lm) Vo : output vol tage from the detector (V) I o : output current from the detector (A) Quantum efficiency number of emitted electrons number of incident photons 1.24 : wavelengt h of the radiation ( m) External Photoelectric Detector Vacuum Photodiode Photocurre nt eP i hc External Photoelectric Detector Photomultiplier Photocurre nt eP i N hc : gain at each dynode N : number of dynodes Internal Photoelectric Detector (Semiconductor Photodiode) P-N photodiode PIN and Avalanche Photodiodes Operating modes: (1) photoconductive mode (reverse biased) (2) Photovoltaic mode (forward biased) Typical Characteristics of Photodetectors Principle of OP Circuit for Photodiodes Light Emitting Diode (LED) Construction Optical design Choice of LED Materials Typical Choice of Materials for LEDs Radiative Transition Through Isoelectronic Centers • For indirect band-gap semiconductors→use recombination of bound excitons at isoelectronic centers to generate radiative recombination • Isoelectronic center : produced by replacing one host atom in the crystal with another kind of atom having the same number of valence electrons • Isoelectronic center attract electron and hole pair → exciton radiative recombination can occur without phonon assistance → hυslightly smaller than bandgap energy Eg • Common isoelectronic centers : • N in GaP → 565 nm • N in GaAs0.35P0.65 → 632 nm • N in GaAs0.15P0.85 → 589 nm • ZnO pair in GaP ( neutral molecular center ) → 700 nm Choice of Substrates for Red and Yellow LEDs Material System for High Brightness Red/Yellow LEDs Choice of Substrates for Blue LEDs • Choices of light emitting material for blue LEDs ( before 1994 ) : GaN system, ZnSe system, SiC, etc. And the winner is : GaN Earlier LED Structures Basic Structures of High Brightness Visible LEDs High Brightness Blue LEDs Radiation pattern Output spectra Note : response time ~ 90ns (yellow and red LED) ~ 500ns (green LED)