Download Pengantar Organisasi Komputer

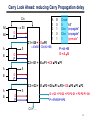
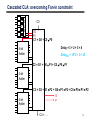
IKI20210
Pengantar Organisasi Komputer
Kuliah No. 23: Aritmatika
Sumber:
1. Hamacher. Computer Organization, ed-4.
2. Materi kuliah CS61C/2000 & CS152/1997, UCB.
18 Desember 2002
Bobby Nazief ([email protected])
Johny Moningka ([email protected])
bahan kuliah: http://www.cs.ui.ac.id/~iki20210/
1
Number Representation
2
Decimal vs. Hexadecimal vs.Binary
° Decimal:
great for humans, especially
when doing arithmetic
° Hex:
if human looking at long
strings of binary numbers, its
much easier to convert to hex
and look 4 bits/symbol
• Terrible for arithmetic; just say no
° Binary:
what computers use;
you learn how computers do
+,-,*,/
• To a computer, numbers always
binary
Unsigned Numbers
Dec Hex Binary
00
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
3
How to Represent Negative Numbers?
° So far, unsigned numbers
° Obvious solution: define leftmost bit to be sign!
• 0 => +, 1 => • Rest of bits can be numerical value of number
° Representation called sign and magnitude
4
Shortcomings of sign and magnitude?
° Arithmetic circuit more complicated
• Special steps depending whether signs are the same or not
° Also, Two zeros
• 0x00000000 = +0ten
• 0x80000000 = -0ten
• What would it mean for programming?
° Sign and magnitude abandoned
5
Another try: complement the bits
° Example: 710 = 001112
-710 = 110002
° Called one’s Complement
° Note: postive numbers have leading 0s, negative
numbers have leadings 1s.
00000
00001 ...
01111
10000 ... 11110 11111
° What is -00000 ?
° How many positive numbers in N bits?
° How many negative ones?
6
Shortcomings of ones complement?
° Arithmetic not too hard
° Still two zeros
• 0x00000000 = +0ten
• 0xFFFFFFFF = -0ten
• What would it mean for programming?
° One’s complement eventually abandoned because
another solution was better
7
Search for Negative Number Representation
° Obvious solution didn’t work, find another
° What is result for unsigned numbers if tried to subtract
large number from a small one?
• Would try to borrow from string of leading 0s,
so result would have a string of leading 1s
• With no obvious better alternative, pick representation that made the
hardware simple: leading 0s  positive, leading 1s  negative
• 000000...xxx is >=0, 111111...xxx is < 0
° This representation called two’s complement
8
Two’s Complement Number line
00000 00001
11111
° 2 N-1 non-negatives
N-1 negatives
11110
°
2
00010
-1 0 1
2
-2
° one zero
° how many positives?
.
.
.
.
.
.
° comparison?
° overflow?
-15 -16 15
10001 10000 01111
9
Two’s Complement Numbers
0000 ... 0000 0000 0000 0000two =
0000 ... 0000 0000 0000 0001two =
0000 ... 0000 0000 0000 0010two =
...
0111 ... 1111 1111 1111 1101two =
0111 ... 1111 1111 1111 1110two =
0111 ... 1111 1111 1111 1111two =
1000 ... 0000 0000 0000 0000two =
1000 ... 0000 0000 0000 0001two =
1000 ... 0000 0000 0000 0010two =
...
1111 ... 1111 1111 1111 1101two =
1111 ... 1111 1111 1111 1110two =
1111 ... 1111 1111 1111 1111two =
0ten
1ten
2ten
2,147,483,645ten
2,147,483,646ten
2,147,483,647ten
–2,147,483,648ten
–2,147,483,647ten
–2,147,483,646ten
–3ten
–2ten
–1ten
° One zero, 1st bit => >=0 or <0, called sign bit
• but one negative with no positive –2,147,483,648ten
10
Two’s Complement Formula
° Can represent positive and negative numbers in terms of
the bit value times a power of 2:
• d31 x -231 + d30 x 230 + ... + d2 x 22 + d1 x 21 + d0 x 20
° Example
1111 1111 1111 1111 1111 1111 1111 1100two
= 1x-231 +1x230 +1x229+... +1x22+0x21+0x20
= -231 + 230 + 229 + ... + 22 + 0 + 0
= -2,147,483,648ten + 2,147,483,644ten
= -4ten
° Note: need to specify width: we use 32 bits
11
Two’s complement shortcut: Negation
° Invert every 0 to 1 and every 1 to 0, then add 1 to the
result
•
•
•
•
Sum of number and its one’s complement must be 111...111two
111...111two= -1ten
Let x’ mean the inverted representation of x
Then x + x’ = -1  x + x’ + 1 = 0  x’ + 1 = -x
° Example: -4 to +4 to -4
x : 1111 1111 1111 1111 1111 1111 1111 1100two
x’: 0000 0000 0000 0000 0000 0000 0000 0011two
+1: 0000 0000 0000 0000 0000 0000 0000 0100two
()’: 1111 1111 1111 1111 1111 1111 1111 1011two
+1: 1111 1111 1111 1111 1111 1111 1111 1100two
12
Two’s comp. shortcut: Sign extension
° Convert 2’s complement number using n bits to
more than n bits
° Simply replicate the most significant bit (sign bit)
of smaller to fill new bits
•2’s comp. positive number has infinite 0s
•2’s comp. negative number has infinite 1s
•Bit representation hides leading bits;
sign extension restores some of them
•16-bit -4ten to 32-bit:
1111 1111 1111 1100two
1111 1111 1111 1111 1111 1111 1111 1100two
13
Addition of Positive Numbers
14
One-Bit Full Adder (1/3)
° Example Binary Addition:
a:
0
0
1
1
b:
0
1
0
1
Sum: 1
0
0
0
Carries
° Thus for any bit of addition:
• The inputs are ai, bi, CarryIni
• The outputs are Sumi, CarryOuti
° Note: CarryIni+1 = CarryOuti
15
One-Bit Full Adder (2/3)
A
0
0
0
0
1
1
1
1
Definition
B CarryIn CarryOut Sum
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
0
0
0
1
0
1
1
0
1
0
1
0
1
1
1
1
Sum = ABC
¯ ¯ in + ABC
¯ ¯ in + ABC
¯ ¯in + ABCin
CarryOut = AB + ACin + BCin
16
One-Bit Full Adder (3/3)
° To create one-bit full adder:
• implement gates for Sum
• implement gates for CarryOut
• connect all inputs with same name
CarryIn
A
+
B
Sum
CarryOut
17
Ripple-Carry Adders: adding n-bits numbers
CarryIn0
A0
B0
A1
B1
A2
B2
A3
B3
1-bit
Sum0
FA
CarryIn1 CarryOut0
1-bit
Sum1
FA
CarryIn2 CarryOut1
1-bit
Sum2
FA
CarryIn3 CarryOut2
1-bit
FA
Sum3
CarryOut3
° Critical Path of n-bit Rippled-carry adder is n*CP
• CP = 2 gate-delays (Cout = AB + ACin + BCin)
18
Overflow
° Binary bit patterns above are simply representatives
of numbers
° Numbers really have an infinite number of digits
• with almost all being zero except for a few of the rightmost digits
• Just don’t normally show leading zeros
° If result of add (or -,*/) cannot be represented by these
rightmost HW bits, overflow is said to have occurred
• When CarryOut is generated from MSB
00000 00001 00010
11110 11111
19
Fast Adders
20
Carry Look Ahead: reducing Carry Propagation delay
Cin
A0
B0
S0
G
P
C1 = G0 + C0  P0
A
B
S
G
P
A
B
A
0
0
1
1
= A0B0 + C0(A0+B0)
B
0
1
0
1
C-out
0
“kill”
C-in “propagate”
C-in “propagate”
1
“generate”
P=A+B
G=AB
C2 = G1 + G0 P1 + C0  P0  P1
S
G
P
C3 = G2 + G1 P2 + G0  P1  P2 + C0  P0  P1  P2
A
B
S
G = G3 + P3·G2 + P3·P2·G1 + P3·P2·P1·G0
G
P
P = P3·P2·P1·P0
C4 = . . .
21
Carry Look Ahead: Delays
° Expression for any carry:
• Ci+1 = Gi + PiGi-1 + … + PiPi-1 … P0C0
° All carries can be obtained in 3 gate-delays:
• 1 needed to developed all Pi and Gi
• 2 needed in the AND-OR circuit
° All sums can be obtained in 6 gate-delays:
• 3 needed to obtain carries
¯ in + ABC
¯ ¯ in + ABC
¯ ¯in + ABCin
• 1 needed to invert carry
Sum = ¯
ABC
• 2 needed in the AND-OR circuit of Sum’s circuit
° Independent of the number of bits (n)
° 4-bit Adder:
• CLA: 6 gate-delays
• RC: (3*2 + 3) gate-delays
° 16-bit Adder:
• CLA: 6 gate-delays
• RC: (15*2 + 3) gate-delays
22
Cascaded CLA: overcoming Fan-in constraint
C
L
A
C0
G0
P0
C1 = G0 + C0  P0
Delay = 3 + 2 + 3 = 8
4-bit
Adder
DelayRC = 15*2 + 3 = 33
C2 = G1 + G0 P1 + C0  P0  P1
4-bit
Adder
C3 = G2 + G1 P2 + G0  P1  P2 + C0  P0  P1  P2
G
P
4-bit
Adder
C4 = . . .
23
Signed Addition & Subtraction
24
Addition & Subtraction Operations
° Subtraction:
° Addition:
• Just add the two numbers
• Ignore the Carry-out from MSB
• Result will be correct, provided
there’s no overflow
• Form 2’s complement of the
subtrahend
• Add the two numbers as in
Addition
0 1 0 1 (+5)
+0 0 1 0 (+2)
0 1 1 1 (+7)
0 1 0 1 (+5)
+1 0 1 0 (-6)
1 1 1 1 (-1)
0 0 1 0 (+2)
0 1 0 0 (+4)
1 0 1 1 (-5)
+1 1 1 0 (-2)
11 0 0 1 (-7)
0 1 1 1 (+7)
+1 1 0 1 (-3)
10 1 0 0 (+4)
1 1 1 0 (-2)
1 0 1 1 (-5)
0010
+1 1 0 0 (-4)
1 1 1 0 (-2)
1110
+0 1 0 1 (+5)
10 0 1 1 (+3)
25
Overflow
Binary
Decimal
2’s Complement
0
0000
0
0000
1
0001
-1
1111
2
0010
-2
1110
3
0011
-3
1101
4
0100
-4
1100
5
0101
-5
1011
6
0110
-6
1010
7
0111
-7
1001
-8
1000
Decimal
° Examples: 7 + 3 = 10 but ...
-4  5 = -9
°
0
+
but ...
1
1
1
1
0
1
1
1
7
0
0
1
1
3
1
0
1
0
–6
+
1
1
0
0
–4
1
0
1
1
–5
0
1
1
1
7
26
Overflow Detection
° Overflow: the result is too large (or too small) to represent
properly
• Example: - 8 < = 4-bit binary number <= 7
° When adding operands with different signs, overflow cannot
occur!
° Overflow occurs when adding:
• 2 positive numbers and the sum is negative
• 2 negative numbers and the sum is positive
° On your own: Prove you can detect overflow by:
• Carry into MSB ° Carry out of MSB
0
+
1
1
1
1
0
1
1
1
7
0
0
1
1
3
1
0
1
0
–6
+
0
1
1
0
0
–4
1
0
1
1
–5
0
1
1
1
7
27
Overflow Detection Logic
° Carry into MSB ° Carry out of MSB
• For a N-bit Adder: Overflow = CarryIn[N - 1] XOR CarryOut[N - 1]
CarryIn0
A0
B0
A1
B1
A2
B2
1-bit
Result0
FA
CarryIn1 CarryOut0
1-bit
Result1
FA
CarryIn2 CarryOut1
1-bit
FA
B3
1-bit
FA
Y
X XOR Y
0
0
0
0
1
1
1
0
1
1
1
0
Result2
CarryIn3
A3
X
Overflow
Result3
CarryOut3
28