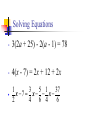Download Notes: Lessons 1, 2, and 4

Analyzing Equations and Inequalities
Objectives:
- evaluate expressions and formulas using order of
operations
- understand/use properties & classifications of
real numbers
- solve equations and inequalities, including those
containing absolute value
Expressions & Formulas
•
•
•
•
ORDER OF OPERATIONS
Parentheses
Exponents
Multiply/Divide from left to right
Add/Subtract from left to right
•
•
•
•
•
Order of Operations
2
Simplify:
[9 ÷ (4 - 7)] - 8
Exponents
[9 ÷ (16 - 7)] - 8
Parentheses
[9 ÷ (9)] - 8
Divide
[1]-8
Subtract
-7
Expressions and Formulas
How do you evaluate expressions and
formulas?
Replace each variable with a value and
then apply the order of operations.
Expressions
Evaluate: a[b2(b + a)]
if a = 12 and b= 1
• Substitute:
12[12(1 + 12)]
• Parentheses:
12[12(13)]
• Exponents:
12[1(13)]
• Parentheses:
12[13]
• Multiply:
156
Properties of Real Numbers
The properties of real numbers
allow us to manipulate expressions
and equations and find the values
of a variable.
Number Classification
•
•
•
•
•
•
Natural numbers are the counting numbers.
Whole numbers are natural numbers and zero.
Integers are whole numbers and their opposites.
Rational numbers can be written as a fraction.
Irrational numbers cannot be written as a
fraction.
All of these numbers are real numbers.
Number Classifications
Subsets of the Real Numbers
Q - Rational
I - Irrational
Z - Integers
W - Whole
N - Natural
Classify each number
-1
6
real, rational, integer
real, rational, integer, whole,
natural
real, irrational
1
2
0
-2.222
real, rational
real, rational, integer, whole
real, rational
Properties of Real Numbers
Commutative Property
• Think… commuting to work.
• Deals with ORDER. It doesn’t matter
what order you ADD or MULTIPLY.
•
•
a+b = b+a
4•6=6•4
Properties of Real Numbers
Associative Property
• Think…the people you associate
with, your group.
• Deals with grouping when you
Add or Multiply.
• Order does not change.
Properties of Real Numbers
Associative Property
•
(a + b) + c = a + ( b + c)
•
(nm)p = n(mp)
Properties of Real Numbers
Additive Identity Property
• s + 0 = s
Multiplicative Identity Property
• 1(b) = b
Properties of Real Numbers
Distributive Property
•
a(b + c) = ab + ac
•
(r + s)9 = 9r + 9s
Name the Property
•
•
•
•
•
5=5+0
5(2x + 7) =
10x + 35
8•7=7•8
24(2) = 2(24)
(7 + 8) + 2 = 2 +
(7 + 8)
Additive Identity
Distributive
Commutative
Commutative
Commutative
Name the Property
•
•
7 + (8 + 2) = (7 + 8) + 2
1 • v + -4 = v + -4
•
(6 - 3a)b =
6b - 3ab
•
•
4(a + b) =
4a + 4b
•
•
•
Associative
Multiplicative
Identity
Distributive
Distributive
Properties of Real Numbers
Reflexive Property
•
a+b=a+b
The same expression is written
on both sides of the equal sign.
Properties of Real Numbers
Symmetric Property
•
If a = b then b = a
•
If 4 + 5 = 9 then 9 = 4 + 5
Properties of Real Numbers
Transitive Property
•
If a = b and b = c then a = c
•
If 3(3) = 9 and 9 = 4 +5,
then 3(3) = 4 + 5
Properties of Real Numbers
Substitution Property
•
If a = b, then a can be
replaced by b.
•
a(3 + 2) = a(5)
Name the property
•
•
•
•
•
•
5(4 + 6) = 20 + 30
5(4 + 6) = 5(10)
5(4 + 6) = 5(4 + 6)
If 5(4 + 6) = 5(10) then
5(10) = 5(4 + 6)
5(4 + 6) = 5(6 + 4)
If 5(10) = 5(4 + 6) and
5(4 + 6) = 20 + 30 then
5(10) = 20 + 30
•
•
•
•
•
•
Distributive
Substitution
Reflexive
Symmetric
Commutative
Transitive
Solving Equations
•
To solve an equation, find
replacements for the variables to
make the equation true.
Each of these replacements is called
a solution of the equation.
Equations may have {0, 1, 2 … }
solutions.
}
•
•
Solving Equations
•
3(2a + 25) - 2(a - 1) = 78
•
4(x - 7) = 2x + 12 + 2x
1
3
5 1
37
 x  7 
x  x
2
4
6 4
6
Solving Equations
2
πr h,
•
Solve: V =
for h
•
Solve: de - 4f = 5g, for e