Download SARS Outbreaks in Ontario, Hong Kong and Singapore: the role of

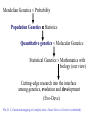
Basic Genetics
(1) Mendelian genetics
How does a gene transmit from a parent to its progeny
(individual)?
(2) Population genetics
How is a gene segregating in a population (a group of
individuals)?
(3) Quantitative genetics
How is gene segregation related with the phenotype of a
character?
(4) Molecular genetics
What is the molecular basis of gene segregation and
transmission?
(5) Developmental genetics
(6) Epigenetics (genetic imprinting)
Genomic Imprinting
The callipygous animals 1 and 3 compared to normal animals 2 and 4
(Cockett et al. Science 273: 236-238, 1996)
Mendelian Genetics  Probability
Population Genetics  Statistics
Quantitative genetics  Molecular Genetics
Statistical Genetics  Mathematics with
biology (our view)
Cutting-edge research into the interface
among genetics, evolution and development
(Evo-Deve)
Wu, R. L. Functional mapping of complex traits. Nature Reviews Genetics (submitted).
Mendel’s Laws
Mendel’s first law
• There is a gene with two alleles on a chromosome location (locus)
• These alleles segregate during the formation of the reproductive
cells, thus passing into different gametes
Diploid
Gene A
A| a |
Centromere
A|
Probability
A pair of chromosomes
½
Gamete
a|
½
Gamete
Mendel’s second law
• There are two or more pairs of genes on different chromosomes
• They segregate independently (partially correct)
Diploid
A|a|, B|b|
Probability
A|, B|
A|, b|
a|, B|
a|, b|
¼
¼
¼
¼
Four two-gene gametes
What about three genes?
Linkage (exception to Mendel’s second law)
• There are two or more pairs of genes located on the same
chromosome
• They can be linked or associated (the degree of association is
described by the recombination fraction)
High linkage
Low linkage
A
B
A
B
How the linkage occurs? – consider two genes A and B
1
2
3
A
a
A Aa
a
B
b
B B b b
A
4
a
A
a
A
a
A
a
B B
b
b
B
B
b
b
Stage 1: A pair of chromosomes, one from the father and the other from the mother
Stage 2: Each chromosome is divided into two sister chromatids
Stage 3: Non-sister chromatids crossover
Stage 4: Meiosis generates four gametes AB, aB, Ab and ab –
Nonrecombinants (AB and ab) and
Recombinants (aB and Ab)
How to measure the linkage? – based on a design
Parents
Gamete
AABB
AB
aabb
ab
×
F1
Gamete
AaBb
AB
Ab
aB
× aabb
ab
ab
Backcross
Observations
AaBb
n1
Aabb
n2
aaBb
n3
aabb
n4
Gamete type
Non-recom/
Parental
Recom/
Non-parental
Recom/
Non-parental
Non-recom/
Parental
Define the proportion of the recombinant gametes over the total gametes as
the recombination fraction (r) between two genes A and B
r = (n2+n3)/(n1+n2+n3+n4)
Several concepts
Genotype and Phenotype
• Locus (loci), chromosomal location of a gene
• Allele (A, a), a copy of gene
• Dominant allele, one allele whose expression inhibits the
expression of its alternative allele
• Recessive allele (relative to dominant allele)
• Dominant gene (AA and Aa are not distinguishable, denoted by
A_)
• Codominant gene (AA, Aa and aa are mutually distinguishable)
• Genotype (AA, Aa or aa)
• Homozygote (AA or aa)
• Heterozygote (Aa)
• Phenotype: trait value
Chromosome and Meiosis
• Chromosome: Rod-shaped structure made of DNA
• Diploid (2n): An organism or cell having two sets of chromosomes or
twice the haploid number
• Haploid (n): An organism or cell having only one complete set of
chromosomes
• Gamete: Reproductive cells involved in fertilization. The ovum is the
female gamete; the spermatozoon is the male gamete.
• Meiosis: A process for cell division from diploid to haploid (2n  n)
(two biological advantages: maintaining chromosome number
unchanged and crossing over between different genes)
• Crossover: The interchange of sections between pairing homologous
chromosomes during meiosis
• Recombination, recombinant, recombination fraction (rate, frequency):
The natural formation in offspring of genetic combinations not present
in parents, by the processes of crossing over or independent
assortment.
Molecular markers
• Genetic markers are DNA sequence
polymorphisms that show Mendelian
inheritance
• Marker types
- Restriction fragment length polymorphism
(RFLP)
- Amplified fragment length polymorphism
(AFLP)
- Simple sequence repeat (SSR)
- Single nucleotide polymorphism (SNP)
Population Genetics
• Different copies of a gene are called alleles; for
example A and a at gene A;
• These alleles form three genotypes, AA, Aa and
aa;
• The allele (or gene) frequency of an allele is
defined as the proportion of this allele among a
group of individuals;
• Accordingly, the genotype frequency is the
proportion of a genotype among a group of
individuals
Calculations of allele frequencies and genotype frequencies
Genotypes
Counts
AA
224
Aa
64
aa
6
Total 294
Estimates genotype frequencies
PAA = 224/294 = 0.762
PAa = 64/294 = 0.218
Paa = 6/294 = 0.020
PAA + PAa + Paa = 1
Allele frequencies
pA = (2214+64)/(2294)=0.871, pa = (26+64)/(2294)=0.129,
pA + pa = 0.871 + 0.129 = 1
Expected genotype frequencies
AA
pA2 = 0.8712
= 0.769
Aa
2pApa = 2  0.871  0.129 = 0.224
Aa
pa2 = 0.1292
= 0.017
Genotypes
AA
Aa
aa
Total
Counts
nAA
nAa
naa
n
Estimates of genotype freq.
PAA = nAA/n
PAa = nAa/n
Paa = naa/n
PAA + PAa + Paa = 1
Allele frequencies
pA = (2nAA + nAa)/2n
pa = (2naa + nAa)/2n
Standard error of the estimate of the allele frequency
Var(pA) = pA(1 - pA)/2n
The Hardy-Weinberg Law
• In the Hardy-Weinberg equilibrium (HWE), the
relative frequencies of the genotypes will remain
unchanged from generation to generation;
• As long as a population is randomly mating, the
population can reach HWE from the second
generation;
• The deviation from HWE, called Hardy-Weinberg
disequilibrium (HWD), results from many factors,
such as selection, mutation, admixture and
population structure…
Mendelian inheritance at the individual level
(1) Make a cross between two individual parents
(2) Consider one gene (A) with two alleles A and a  AA, Aa, aa
Thus, we have a total of nine possible cross combinations:
1.
2.
3.
4.
5.
6.
7.
8.
9.
Cross
AA  AA
AA  Aa
AA  aa
Aa  AA
Aa  Aa
Aa  aa
aa  AA
aa  Aa
aa  aa









Mendelian segregation ratio
AA
½AA + ½Aa
Aa
½AA + ½Aa
¼AA + ½Aa + ¼aa
½Aa + ½aa
Aa
½Aa + ½aa
aa
Mendelian inheritance at the population level
• A population, a group of individuals, may contain all these nine
combinations, weighted by the mating frequencies.
• Genotype frequencies: AA, PAA; Aa, PAa; aa, Paa
Cross
1.
2.
3.
4.
5.
6.
7.
8.
9.
AA  AA
AA  Aa
AA  aa
Aa  AA
Aa  Aa
Aa  aa
aa  AA
aa  Aa
aa  aa
Mating freq. (t)
PAA(t)PAA(t)
PAA(t)PAa(t)
PAA(t)Paa(t)
PAa(t)PAA(t)
PAa(t)PAa(t)
PAa(t)Paa(t)
Paa(t)PAA(t)
Paa(t)PAa(t)
Paa(t)Paa(t)









Mendelian segreg. ratio (t+1)
AA
Aa
aa
1
0
0
½
½
0
0
1
0
½
½
0
¼
½
¼
0
½
½
0
1
0
0
½
½
0
0
1
PAA(t+1) = 1[PAA(t)]2 + ½ 2[PAA(t)PAa(t)] + ¼[PAa(t)]2
= [PAA(t) + ½PAa(t)]2
Similarly, we have
Paa(t+1) = [Paa(t) + ½PAa(t)]2
PAa(t+1) = 2[PAA(t) + ½PAa(t)][Paa(t) + ½PAa(t)]
Therefore, we have
[PAa(t+1)]2 = 4PAA(t+1)Paa(t+1)
Furthermore, if random mating continues, we have
PAA(t+2) = [PAA(t+1) + ½PAa(t+1)]2 = PAA(t+1)
PAa(t+2) = 2[PAA(t+1) + ½PAa(t+1)][Paa(t+1) + ½PAa(t+1)] = PAa(t+1)
Paa(t+2) = [Paa(t+1) + ½PAa(t+1)]2 = Paa(t+1)
Concluding remarks
A population with [PAa(t+1)]2 = 4PAA(t+1)Paa(t+1) is said to be in
Hardy-Weinberg equilibrium (HWE). The HWE population has the
following properties:
(1) Genotype (and allele) frequencies are constant from generation to
generation,
(2) Genotype frequencies = the product of the allele frequencies, i.e.,
PAA = pA2, PAa = 2pApa, Paa = pa2
For a population at Hardy-Weinberg disequilibrium (HWD), we have
• PAA = pA2 + D
• PAa = 2pApa – 2D
• Paa = pa2 + D
The magnitude of D determines the degree of HWD.
• D = 0 means that there is no HWD.
• D has a range of max(-pA2 , -pa2)  D  pApa
Chi-square test for HWE
• Whether or not the population deviates from
HWE at a particular locus can be tested using
a chi-square test.
• If the population deviates from HWE (i.e.,
Hardy-Weinberg disequilibrium, HWD), this
implies that the population is not randomly
mating. Many evolutionary forces, such as
mutation, genetic drift and population
structure, may operate.
Example 1
AA
Obs 224
Exp n(pA2) = 222.9
Aa
64
n(2pApa) = 66.2
aa
6
n(pa2) = 4.9
Total
294
294
Test statistics
x2 =  (obs – exp)2 /exp = (224-222.9)2/222.9 + (64-66.2)2/66.2 +
(6-4.9)2/4.9 = 0.32
is less than
x2df=1 ( = 0.05) = 3.841
Therefore, the population does not deviate from HWE at this locus.
Why the degree of freedom = 1? Degree of freedom = the
number of parameters contained in the alternative hypothesis –
the number of parameters contained in the null hypothesis. In this
case, df = 2 (pA or pa and D) – 1 (pA or pa) = 1
Example 2
Obs
Exp
AA
234
n(pA2)
= 230.1
Aa
36
n(2pApa)
= 43.8
aa
6
n(pa2)
= 2.1
Total
276
276
Test statistics
x2 =  (obs – exp)2/exp = (234-230.1)2/230.1 + (3643.8)2/43.8 + (6-2.1)2/2.1 = 8.8
is greater than x2df=1 ( = 0.05) = 3.841
Therefore, the population deviates from HWE at this
locus.
Linkage disequilibrium
• Consider two loci, A and B, with alleles A, a and B, b,
respectively, in a population
• Assume that the population is at HWE
• If the population is at Hardy-Weinberg equilibrium,
we have
Gene A
AA: PAA = pA2
Aa: PAa = 2pApa
Aa: Paa = pa2
PAA+PAa+Paa = 1
pA + pa = 1
Gene B
BB: PBB = pB2
Bb: PBb = 2pBpb
bb: Pbb = pb2
PBB+PBb+Pbb=1
pB + p b = 1
But the population is at Linkage Disequilibrium (for a
pair of loci). Then we have
• Two-gene haplotype AB:
pAB = pApB + DAB
• Two-gene haplotype Ab:
pAb = pApb + DAb
• Two-gene haplotype aB:
paB = papB + DaB
• Two-gene haplotype ab:
pab = papb + Dab
pAB+pAb+paB+pab = 1
Dij is the coefficient of linkage disequilibrium (LD)
between the two genes in the population. The
magnitude of D reflects the degree of LD. The larger
D, the stronger LD.
pA = pAB+pAb
= pApB + DAB + pApb + DAb
= pA+DAB+DAb
pB = pAB+paB
= pB+DAB+DaB
pb = pAb+pab
= pb+DaB+Dab

DAB = -DAb

DAB = -DaB

Dab = -DaB
Finally, we have DAB = -DAb = -DaB = Dab = D.
Re-write four two-gene haplotypes
• AB: pAB = pApB + D
• Ab: pAb = pApb – D
• aB: paB = papB – D
• ab: pab = papb + D
D = pABpab - pAbpaB
D = 0  the population is at the linkage equilibrium
How does D transmit from one generation (1) to the
next (2)?
D(2) = (1-r)1 D(1)
…
D(t+1) = (1-r)t D(1)
t, D(t+1)  r
Proof to D(t+1) = (1-r)1 D(t)
•
The four gametes randomly unite to form a zygote. The proportion 1-r of the
gametes produced by this zygote are parental (or nonrecombinant) gametes and
fraction r are nonparental (or recombinant) gametes. A particular gamete, say AB,
has a proportion (1-r) in generation t+1 produced without recombination. The
frequency with which this gamete is produced in this way is (1-r)pAB(t).
•
Also this gamete is generated as a recombinant from the genotypes formed by the
gametes containing allele A and the gametes containing allele B. The frequencies
of the gametes containing alleles A or B are pA(t) and pB(t), respectively. So the
frequency with which AB arises in this way is rpA(t)pB(t).
•
Therefore the frequency of AB in the generation t+1 is
pAB(t+1) = (1-r)pAB(t) + rpA(t)pB(t)
By subtracting is pA(t)pB(t) from both sides of the above equation, we have
D(t+1) = (1-r)1 D(t)
Whence
D(t+1) = (1-r)t D(1)
Estimate and test for LD
Assuming random mating in the population, we have joint probabilities of the two genes
BB (PBB)
Bb (PBb)
bb (Pbb)
_______________________________________________________________________________________
AA (PAA)
pAB2
2PABPAb
PAb2
n22
n21
n20
Aa (PAa)
2PABPaB
2(PABPab+PAbPaB)
2PAbPab
n12
n11
n10
2
aa (Paa)
PaB
2PAbPab
Pab2
n02
n01
n00
________________________________________________________________________________________
Multinomial pdf
H1: D  0
log f(pij|n)
= log n!/(n22!…n00!)
+ n22 log pAB2 + n21log (2pABpAb) + n20 log pAb2
+…
Estimate pAB, pAb, paB (pab = 1-pAB-pAb-paB)  pA, pB, D
H0: D = 0
log f(pi,pj|n)
= log n!/(n22!…n00!)
+ n22log(pApB)2 + n21log(2pA2pBpb)+n20log(pApb)2
+…
Estimate pA and pB.
Chi-square Test of Linkage Disequilibrium (D)
Test statistic
x2 = 2nD2/(pApapBpb)
is compared with the critical threshold value obtained
from the chi-square table x2df=1 (0.05). n is the number
of individuals in the population.
If x2 < x2df=1 (0.05), this means that D is not significantly
different from zero and that the population under
study is in linkage equilibrium.
If x2 > x2df=1 (0.05), this means that D is significantly
different from zero and that the population under
study is in linkage disequilibrium.
Example
(1) Two genes A with allele A and a, B with alleles B and b, whose population
frequencies are denoted by pA, pa (=1- pA) and pB, pb (=1- pb), respectively
(2) These two genes are associated with each other, having the coefficient of
linkage disequilibrium D
Four gametes are observed as follows:
Gamete
AB
Obs
474
Gamete frequency pAB
Ab
611
pAb
aB
142
paB
ab
773
pab
Total
2n=2000
=474/2000 =611/2000 =142/2000 =773/2000
=0.237 =0.305 =0.071 =0.386
1
Estimates of allele frequencies
pA = pAB + pAb = 0.237 + 0.305 = 0.542
pa = paB + pab = 0.071 + 0.386 = 0.458
pB = pAB + paB = 0.237 + 0.071 = 0.308
pb = pAb + pab = 0.305 + 0.386 = 0.692
The estimate of D
D = pABpab – pAbpaB = 0.237  0.386 – 0.305  0.071 = 0.0699
Test statistics
x2 = 2nD2/ (pApapBpb)
=210000.06992/(0.5420.4580.3080.692) = 184.78 is
greater than x2df=1 (0.05) = 3.841.
Therefore, the population is in linkage disequilibrium
at these two genes under consideration.
A second approach for calculating x2:
Gamete
Obs
Exp
AB
474
2n(pApB)
=334.2
Ab
aB
611
142
2n(pApb) 2n(papB)
=750.8 =281.8
ab
773
2n(papb)
=633.2
Total
2n=2000
2000
x2 =  (obs – exp)2 /exp
= (474-334.2)2/334.2 + (611-750.8)2/750.8 + (142-281.8)2/281.8 + (773-633.2)2/633.2
= 184.78
= 2nD2/ (pApapBpb)
Measures of linkage disequilibrium
(1) D, which has a limitation that its value depends on
the allele frequencies
•
•
D = 0.02 is considered to be
large for two genes each with diverse allele
frequencies, e.g., pA = pB = 0.9 vs. pa = pb = 0.1
small for two genes each with similar allele
frequencies, e.g., pA = pB = 0.5 vs. pa = pb = 0.5
(2) To make a comparison between gene pairs with
different allele frequencies, we need a new
normalized measure.
The range of LD is
max(-pApB, -papb)  D  min(pApb, papB)
The normalized LD (Lewontin 1964) is defined as
D' = D/ Dmax,
where Dmax is the maximum that D can have, which is
Dmax =
max(-pApB, -papb) if D < 0,
or min(pApb, papB)
if D > 0.
(3) Linkage disequilibrium measured as the correlation
between the A and B alleles
R = D/(pApapBpb),
r: [-1, 1]
Note: x2= 2nR2 follows the chi-square distribution
with df = 1 under the null hypothesis of D = 0.
For the above example, we have
R = 0.0699/(pApbpapB) = 0.3040.
Application of LD analysis
D(t+1) = (1-r)tD(t),
This means that when the population undergoes random
mating, the LD decays exponentially in a proportion
related to the recombination fraction.
(1) Population structure and evolution
Estimating D, D' and R  the mating history of
population
The larger the D’ and R estimates, the more likely the population in
nonrandom mating, the more likely the population to have a small
size, the more likely the population to be affected by evolutionary
forces.
Human origin studies based on LD analysis
Reich, D. E., M. Cargill, S. Bolk, J. Ireland, P. C. Sabeti, D. J. Richter, T. Lavery,
R. Kouyoumjian, S. F. Farhadian, R. Ward and E. S. Lander, 2001 Linkage
disequilibrium in the human genome. Nature 411: 199-204.
Dawson, E., G. R. Abecasis, S. Bumpstead, Y. Chen et al. 2002 A first-generation
linkage disequilibrium map of human chromosome 22. Nature 418: 544-548.
LD curve for Swedish and Yoruban samples.
To minimize ascertainment bias, data are only
shown for marker comparisons involving the
core SNP. Alleles are paired such that D' > 0
in the Utah population. D' > 0 in the other
populations indicates the same direction of
allelic association and D' < 0 indicates the
opposite association. a, In Sweden, average
D' is nearly identical to the average |D'|
values up to 40-kb distances, and the overall
curve has a similar shape to that of the Utah
population (thin line in a and b). b, LD
extends less far in the Yoruban sample, with
most of the long-range LD coming from a
single region, HCF2. Even at 5 kb, the average
values of |D'| and D' diverge substantially. To
make the comparisons between populations
appropriate, the Utah LD curves are calculated
solely on the basis of SNPs that had been
successfully genotyped and met the minimum
frequency criterion in both populations
(Swedish and Yoruban) (Reich,te al. 2001)
(2) Fine mapping of disease genes
The detection of LD may imply that the
recombination fraction between two genes
is small and therefore closer (given the
assumption that t is large).
Quantitative genetics
•
•
•
•
•
•
•
•
Many traits that are important in agriculture, biology
and biomedicine are continuous in their phenotypes.
For example,
Crop Yield
Stemwood Volume
Plant Disease Resistances
Body Weight in Animals
Fat Content of Meat
Time to First Flower
IQ
Blood Pressure
The following image demonstrates the variation for flower
diameter, number of flower parts and the color of the flower
Gaillaridia pilchella (McClean 1997). Each trait is controlled
by a number of genes each interacting with each other and an
array of environmental factors.
Number of Genes
Number of Genotypes
1
2
5
10
3
9
243
59,049
Consider two genes, A with two alleles A and a, and B with two
alleles B and b.
- Each of the alleles will be assigned metric values
- We give the A allele 4 units and the a allele 2 units
- At the other locus, the B allele will be given 2 units and the b allele 1 unit
Genotype
AABB
AABb
AAbb
AaBB
AaBb
Aabb
aaBB
aaBb
aabb
Ratio
1
2
1
2
4
2
1
2
1
Metric value
12
11
10
10
9
8
8
7
6
A grapical format is used to present
the above results:
Normal distribution of a quantitative
trait may be due to
• Many genes
• Environmental effects
The traditional view: polygenes each with small
effect and being sensitive to environments
The new view: A few major gene and many
polygenes (oligogenic control), interacting with
environments
Traditional quantitative genetics research:
Variance component partitioning
• The phenotypic variance of a quantitative trait can be
partitioned into genetic and environmental variance
components.
• To understand the inheritance of the trait, we need to
estimate the relative contribution of these two components.
• We define the proportion of the genetic variance to the
total phenotypic variance as the heritability (H2).
- If H2 = 1.0, then the trait is 100% controlled by genetics
- If H2 = 0, then the trait is purely affected by environmental factors.
•
Fisher (1918) proposed a theory for partitioning
genetic variance into additive, dominant and
epistatic components;
•
Cockerham (1954) explained these genetic variance
components in terms of experimental variances
(from ANOVA), which makes it possible to estimate
additive and dominant components (but not the
epistatic component);
•
I proposed a clonal design to estimate additive,
dominant and part-of-epistatic variance components
Wu, R., 1996 Detecting epistatic genetic variance with a clonally
replicated design: Models for low- vs. high-order nonallelic interaction.
Theoretical and Applied Genetics 93: 102-109.
Genetic Parameters: Means and (Co)variances
One-gene model
Genotype
Genotypic value
Net genotypic value
aa
G0
-a
0
Aa
G1
d
AA
G2
a
origin=(G0+G1)/2
a = additive genotypic value
d = dominant genotypic value
Environmental deviation
E0
E1
E2
Phenotype or
Phenotypic value
Y0=G0+E0
Y1=G1+E1
Y2=G2+E2
Letting =a+(q-p)d
P0
=q2
-a - 
=-2p[a+(q-p)d]
-2p2d
=-2p-2p2d
P1
=2pq
d-
= (q-p)[a+(q-p)d]
+2pqd
=(q-p)+2pqd
P2
=p2
a-
= 2q[a+(q-p)d]
-2q2d
=2q-2q2d
Breeding value
Dominant deviation
-2p
-2p2d
(q-p)
2pqd
2q
-2q2d
Genotype frequency
at HWE
Deviation from population mean 
Population mean  = q2(-a) + 2pqd + p2a = (p-q)a+2pqd
Genetic variance 2g = q2(-2p-2p2d)2 + 2pq[(q-p)+2pqd]2 + p2(2q-2q2d)2
= 2pq2
+
(2pqd)2
= 2a (or VA)
+
2d (or VD)
Additive genetic variance,
Dominant genetic variance,
depending on both on a and d
depending only on d
Phenotypic variance 2P = q2Y02 + 2pqY12 + p2Y22 – (q2Y0 + 2pqY1 + p2Y2)2
Define
H2 = 2g /2P as the broad-sense heritability
h2 = 2a / 2P as the narrow-sense heritability
These two heritabilities are important in understanding the relative
contribution of genetic and environmental factors to the overall
phenotypic variance.
What is  = a+(q-p)d?
It is the average effect due to the substitution of gene from one
allele (A say) to the other (a).
Event A
a contains two possibilities
Frequency
Value change
From Aa to aa
q
d-(-a)
a-d
 = q[d-(-a)]+p(a-d)
= a+(q-p)d
From AA to Aa
p
Midparent-offspring correlation
____________________________________________________________________
Progeny
Genotype
Freq. of
Midparent
AA
Aa
aa
Mean value
of parents
matings
value
a
d
-a
of progeny
____________________________________________________________________
AA × AA
p4
a
1
a
AA × Aa
4p3q
½(a+d)
½
½
½(a+d)
AA × aa
2p2q2
0
1
d
Aa × Aa
4p2q2
d
¼
½
¼
½d
Aa × aa
4pq3
½(-a+d)
½
½
½(-a+d)
aa × aa
q4
-a
1
-a
________________________________________________
Covariance between midparent and offspring:
Cov(OP¯)
= E(OP¯) – E(O)E(P¯)
= p4a a + 4p3q ½(a+d) ½(a+d) + … + q4 (-a)(-a) – [(p-q)a+2pqd]2
= pq2
= ½2a
The regression of offspring on midparent values is
b = Cov(OP¯)/2(P¯)
= ½2a / ½2P
= 2a /2P
= h2
where 2(P¯)=½2P is the variance of midparent value.
IMPORTANT
The regression of offspring on
midparent values can be used to
measure the heritability!
This is a fundamental contribution
by R. A. Fisher.
You can derive other relationships
Degree of relationship
Covariance
____________________________________________________
Offspring and one parent
Cov(OP) = 2a/2
Half siblings
Cov(FS) = 2a/4
Full siblings
Cov(FS) = 2a/2 + 2a/4
Monozygotic twins
Cov(MT) = 2a + 2d
Nephew and uncle
Cov(NU) = 2a/4
First cousins
Cov(FC) = 2a /8
Double first cousins
Cov(DFC) = 2a/4 + 2d/16
Offspring and midparent
Cov(O) = 2a/2
____________________________________________________