* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture powerpoint
Coriolis force wikipedia , lookup
Brownian motion wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Specific impulse wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Angular momentum operator wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Tensor operator wikipedia , lookup
Jerk (physics) wikipedia , lookup
Classical mechanics wikipedia , lookup
Atomic theory wikipedia , lookup
N-body problem wikipedia , lookup
Fictitious force wikipedia , lookup
Angular momentum wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Seismometer wikipedia , lookup
Center of mass wikipedia , lookup
Equations of motion wikipedia , lookup
Moment of inertia wikipedia , lookup
Classical central-force problem wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Centripetal force wikipedia , lookup
Hunting oscillation wikipedia , lookup
Mass versus weight wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Relativistic mechanics wikipedia , lookup
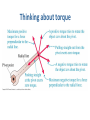
PHY 2048C General Physics I with lab Spring 2011 CRNs 11154, 11161 & 11165 Dr. Derrick Boucher Assoc. Prof. of Physics Sessions 16, Chapter 12 Chapter 12 Homework Due Thursday 3/17 @ midnight (previously Wednesday 3/16) Chapter 12 Practice Problems 9, 13, 15, 21, 23, 33, 35, 37, 49, 73, 87 Unless otherwise indicated, all practice material is from the “Exercises and Problems” section at the end of the chapter. (Not “Questions.”) Chapter 12. Basic Content and Examples Rotational Motion The figure shows a wheel rotating on an axle. Its angular velocity is The units of ω are rad/s. If the wheel is speeding up or slowing down, its angular acceleration is The units of α are rad/s2. Rotational Motion Rotation About the Center of Mass An unconstrained object (i.e., one not on an axle or a pivot) on which there is no net force rotates about a point called the center of mass. The center of mass remains motionless while every other point in the object undergoes circular motion around it. Rotation About the Center of Mass The center of mass is the mass-weighted center of the object. Rotation About the Center of Mass For discrete masses (not a continuous piece of matter but several masses attached together) this simplifies to: Rotational Energy A rotating rigid body has kinetic energy because all atoms in the object are in motion. The kinetic energy due to rotation is called rotational kinetic energy. Here the quantity I is called the object’s moment of inertia. The units of moment of inertia are kg m2. An object’s moment of inertia depends on the axis of rotation. Center of Mass and Motion The “particle model” is a simplification of the motions of real objects, but the center of mass concept allows us to describe the OVERALL translational motion of any object as the motion of its center of mass. Example #1, Problem 12-14, p. 378 Torque Consider the common experience of pushing open a door. Shown is a top view of a door hinged on the left. Four pushing forces are shown, all of equal strength. Which of these will be most effective at opening the door? The ability of a force to cause a rotation depends on three factors: 1. the magnitude F of the force. 2. the distance r from the point of application to the pivot. 3. the angle at which the force is applied. Torque Let’s define a new quantity called torque τ (Greek tau) as Thinking about torque The moment (lever) arm Analogies between Linear and Rotational Dynamics In the absence of a net torque (τnet = 0), the object either does not rotate (ω = 0) or rotates with constant angular velocity (ω = constant). Example #2, Problem 12-24, p. 379 Problem-Solving Strategy: Rotational Dynamics Problems CLICKER Example #3, Problem 12-30, p. 379 The 200 g model rocket shown in the figure generates 4.0 N of thrust. It spins in a horizontal circle at the end of a 100 g rigid rod. What is its angular acceleration in rad/s2 ? Problem-Solving Strategy: Static Equilibrium Problems Example #4, Problem (made-up) equilibrium Section 12.9 rolling Section 12.11 ang. Momentum and conservation The Right-Hand Rule Sometimes called the “Right-hand Screw Rule”, it is a sign convention for depicting rotational motion in vector form. You may recall “righty-tighty, lefty-loosey.” This is for right-handed screws. (And refers to the top of the screw as viewed by the mechanic.) Better is “clockwise-tighty, counterclockwise-loosey.” Question: are there left-handed screws? If so, where? Thanks to Amy Whicker for finding the cool website that has lots of these animations. Example #5, Problem 12-90, p. 383 Chapter 12. Clicker review A new way of multiplying two vectors is introduced in this chapter. What is it called? A. Dot Product B. Scalar Product C. Tensor Product D. Cross Product E. Angular Product Moment of inertia is A. the rotational equivalent of mass. B. the point at which all forces appear to act. C. the time at which inertia occurs. D. an alternative term for moment arm. A rigid body is in equilibrium if A. B. C. neither A nor B. D. either A or B. E. both A and B.