Download File

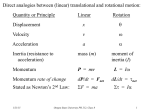
Chapter 9
What causes a change of motion?
In linear motion, we discussed the fact that the net force acting
on an object causes a change in motion. When considering rotational
motion, we need to discuss the cause of angular acceleration.
Consider the following situation
•If both forces represent equal
magnitudes, what will the difference
in motion be?
•α is proportional to force
•α is also proportional to the
perpendicular distance from the axis
of rotation to the line along which
the force acts
•the LEVER ARM or MOMENT ARM is
this perpendicular distance

Lever Arm – more specifically, the distance
which is perpendicular both to the axis of
rotation and to an imaginary line drawn along
the direction of the force.
Which force is
most effective?
Why?





It may be conceptually easier to solve for F⊥ than
for r⊥. Either way, your product will be the same
because the force acts along the lever arm, so sinθ
will be the same.
If more than one torque acts on a body, α is
proportional to the net torque
+ counterclockwise
- Clockwise
SI unit for torque is mN
τ = r⊥F
τ = rF⊥
τ = rFsinθ
•
•
•
•
•
A body is in equilibrium when the sum of the
external forces is zero and when the sum of the
external torques is zero.
In other words…∑τ = 0
Hint: When acceleration is zero the net force and
in the case of rotational motion, net torque is
zero.
Remember the lever arm must be determined
relative to the axis of rotation.
In problem solving, choosing the direction of an
unknown force backward in the free-body
diagram simply means that the value determined
for the force will be a negative number.


The center of gravity of a rigid body is the
point at which its weight can be considered to
act when the torque to the weight is being
calculated.
When weight is the force causing torque, the
center of gravity will be the geometric center
for objects with symmetrical shaped and
weight distributed uniformly. Here τ =
W(L/2)
When finding cg for more than one object, as
in the diagrams, calculate the net torque
created by the board and box about an axis
that is picked arbitrarily to be at the right end
of the board.
x cg
W1 X 1  W2 X 2  ...

W1  W2  ...
If the distribution of weight changes,
the equilibrium may be “knocked off
balance.”


Relating Newton’s 2nd Law for tangential force
and acceleration to torque, we can derive a
rotational motion equation for Newton’s 2nd
Law.
Use rad/s2
  (mr )
2
•
•
•
When using F=ma, we are describing a single
particle.
When using equations relating to torque, it is
often convenient to describe the object
rotating about an axis as a whole.
The moment of inertia can be used to
describe any object rotating about a fixed
axis, not just a particle.
I  mr
2
SI unit for I is kgm2




Recall that all mass has inertial properties.
The rotational analogy to mass is the moment
of inertia.
The sum of the individual moments of inertia
of all the particles will yield the moment of
inertia of the body.
Table 9.1 on pg. 262 summarizes equations
for I specific derived for specific shapes.
  I
α must be expressed in rad/s2
Definition of Rotational
Work



The rotational work Wr
done by a constant
torque in turning an
object through an
angle.
θ must be in radians
SI Unit: joule (j)
W r 
Definition of Rotational
Kinetic Energy
• The rotational kinetic energy KER
of a rigid object rotating with an
angular speed ω about a fixed axis
and having a moment of inertia can
be derived using rotational
variables.
• ω must be in rad/s
•SI unit: joule (j)
1 2
KER  I
2



Recall the law of conservation of energy can
be applied to mechanical energy
In the past we used total mechanical energy
as kinetic energy + potential energy.
The real story for objects experiencing
rotational energy is that the total
mechanical energy will be equal to kinetic
energy + rotational kinetic energy +
potential energy
1
1 2
2
ET  mv  I  mgh
2
2
When a hollow cylinder
and a solid cylinder are
rolled down an incline, the
solid cylinder will reach the
bottom first. This will
happen because the solid
cylinder will have a greater
translational speed.




Linear momentum can be expressed as the
product of mass x velocity.
For rotational motion, the analogous concept
is angular momentum (L).
Again, ω must be expressed in rad/s.
SI unit: kgm2/s
L  I


The total angular momentum of a system remains
constant (is conserved) if the net average external
torque acting on the system is zero.
An ice skater will have a higher angular velocity
when she bring her arms inward because she is
decreasing her radius, thus decreasing her moment
of inertia.
L f  Li