Download Lecture powerpoint

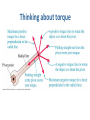
PHY 2048C
General Physics I with lab
Spring 2011
CRNs 11154, 11161 & 11165
Dr. Derrick Boucher
Assoc. Prof. of Physics
Sessions 16, Chapter 12
Chapter 12 Homework
Due Thursday 3/17 @ midnight
(previously Wednesday 3/16)
Chapter 12
Practice Problems
9, 13, 15, 21, 23, 33, 35, 37, 49, 73, 87
Unless otherwise indicated, all practice
material is from the “Exercises and Problems”
section at the end of the chapter. (Not
“Questions.”)
Chapter 12. Basic Content and
Examples
Rotational Motion
The figure shows a wheel
rotating on an axle. Its
angular velocity is
The units of ω are rad/s. If
the wheel is speeding up
or slowing down, its
angular acceleration is
The units of α are rad/s2.
Rotational Motion
Rotation About the Center of
Mass
An unconstrained object
(i.e., one not on an axle
or a pivot) on which there
is no net force rotates
about a point called the
center of mass. The
center of mass remains
motionless while every
other point in the object
undergoes circular
motion around it.
Rotation About the Center of
Mass
The center of mass is the mass-weighted center of the
object.
Rotation About the Center of
Mass
For discrete masses (not a continuous piece of matter
but several masses attached together) this simplifies
to:
Rotational Energy
A rotating rigid body has kinetic energy because all
atoms in the object are in motion. The kinetic energy
due to rotation is called rotational kinetic energy.
Here the quantity I is called the object’s moment of
inertia.
The units of moment of inertia are kg m2. An object’s
moment of inertia depends on the axis of rotation.
Center of Mass and Motion
The “particle model” is a simplification of the motions
of real objects, but the center of mass concept allows
us to describe the OVERALL translational motion of
any object as the motion of its center of mass.
Example #1, Problem 12-14, p. 378
Torque
Consider the common experience of pushing open a
door. Shown is a top view of a door hinged on the left.
Four pushing forces are shown, all of equal strength.
Which of these will be most effective at opening the
door?
The ability of a force to cause a rotation depends on
three factors:
1. the magnitude F of the force.
2. the distance r from the point of application to the
pivot.
3. the angle at which the force is applied.
Torque
Let’s define a new quantity called torque τ (Greek
tau) as
Thinking about torque
The moment (lever) arm
Analogies between Linear and
Rotational Dynamics
In the absence of a net torque (τnet = 0), the
object either does not rotate (ω = 0) or rotates
with constant angular velocity (ω = constant).
Example #2, Problem 12-24, p. 379
Problem-Solving Strategy: Rotational
Dynamics Problems
CLICKER Example #3, Problem 12-30, p. 379
The 200 g model rocket shown in the figure generates
4.0 N of thrust. It spins in a horizontal circle at the end
of a 100 g rigid rod. What is its angular acceleration in
rad/s2 ?
Problem-Solving Strategy: Static
Equilibrium Problems
Example #4, Problem (made-up)
equilibrium
Section 12.9 rolling
Section 12.11 ang. Momentum
and conservation
The Right-Hand Rule
Sometimes called the “Right-hand Screw Rule”, it is a
sign convention for depicting rotational motion in
vector form.
You may recall “righty-tighty, lefty-loosey.” This is for
right-handed screws. (And refers to the top of the
screw as viewed by the mechanic.) Better is
“clockwise-tighty, counterclockwise-loosey.” Question:
are there left-handed screws? If so, where?
Thanks to Amy Whicker for finding the cool website that has lots of
these animations.
Example #5, Problem 12-90, p. 383
Chapter 12. Clicker review
A new way of multiplying two vectors is
introduced in this chapter. What is it
called?
A. Dot Product
B. Scalar Product
C. Tensor Product
D. Cross Product
E. Angular Product
Moment of inertia is
A. the rotational equivalent of mass.
B. the point at which all forces appear to act.
C. the time at which inertia occurs.
D. an alternative term for moment arm.
A rigid body is in equilibrium if
A.
B.
C. neither A nor B.
D. either A or B.
E. both A and B.